配方法解一元二次方程[上学期]
文档属性
| 名称 | 配方法解一元二次方程[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 77.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-09-09 11:20:00 | ||
图片预览

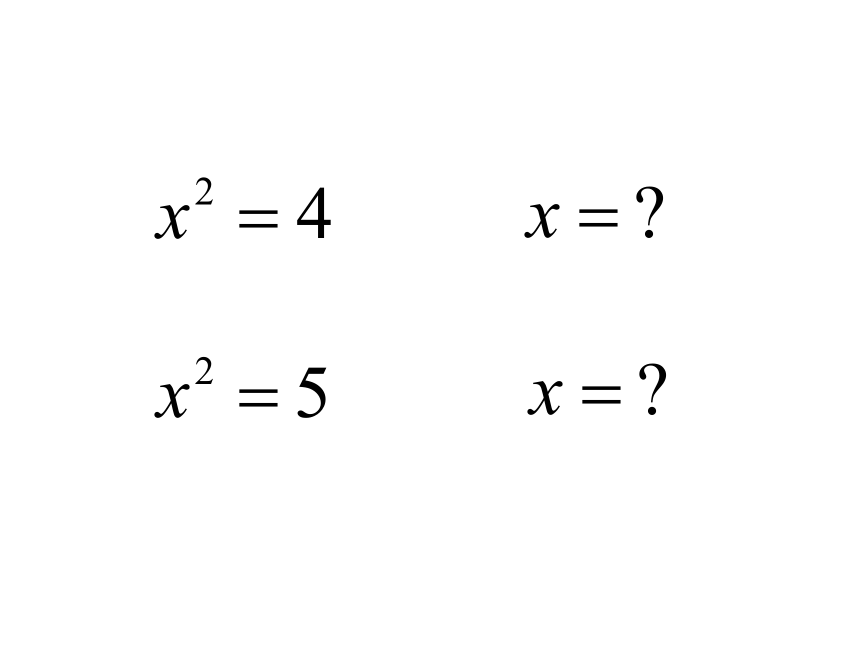




文档简介
课件19张PPT。解一元二次方程配方法 一般地,对于形如x2=a(a≥0)的方程,
根据平方根的定义,可解得
这种解一元二次方程的方法叫做开平方法.例1.用开平方法解下列方程:
(1)3x2-27=0;
(2)(2x-3)2=49
一元一次方程的根是唯一的,而一元二次方程的根却有两个。巩固练习 1(1)方程 的根是
(2)方程 的根是
(3) 方程 的根是 2. 选择适当的方法解下列方程:
(1)x2- 81=0 (2) x2 =50
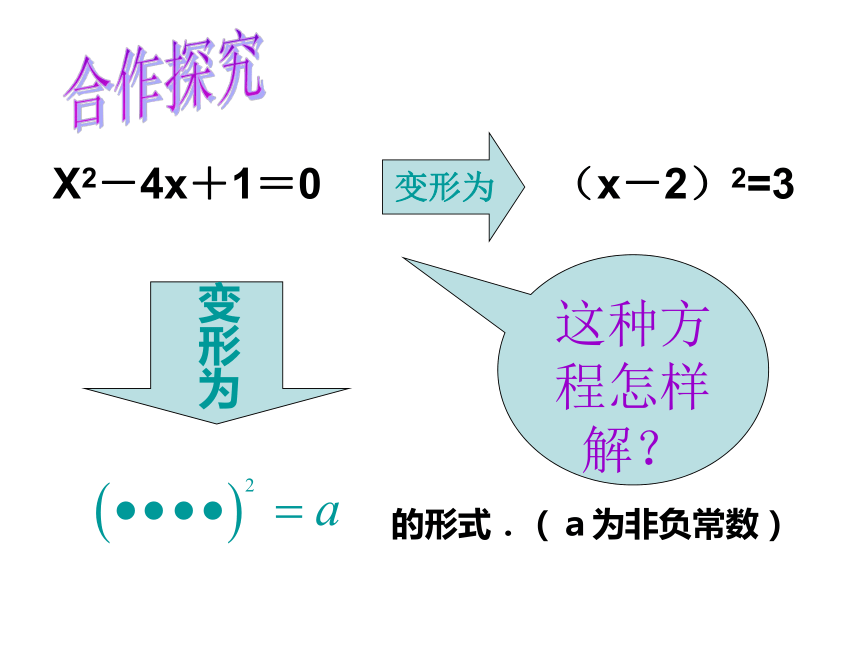
(3)(x+1)2=4 (4)x2+2 x+5=0X1=0.5, x2=-0.5X1=3, x2=—3X1=2, x2=-1合作探究这种方程怎样解?变形为的形式.(a为非负常数)变形为X2-4x+1=0(x-2)2=3 把一元二次方程的左边配成一个完全平方式,然后用开平方法求解,这种解一元二次方程的方法叫做配方法.(1)x2+8x+ =(x+4)2
(2)x2-4x+ =(x- )2
(3)x2-___x+ 9 =(x- )2填空 配方时, 等式两边同时加上的是一次项系数一半的平方。166342。填空: 253656例2:用配方法解下列方程二次项系数为1二次项系数不为1可以先将系数化为1 ,移项,得 配方,得 由此可得 移项,得 配方得 由此可得 移项,得 二次项系数化为1,得 配方得 由此可得 移项,得 二次项系数化为1,得 配方得 用配方法解一元二次方程的步骤:移项:把常数项移到方程的右边;
系数化为1:将二次项系数化为1;
配方:方程两边都加上一次项系数一半的平方;
开方:根据平方根意义,方程两边开平方;
求解:解一元一次方程;
定解:写出原方程的解.练一练1(1)(2)(3)(4)练一练3(1)(2)(3)(4)(5)(6)练一练4(看谁快而准!)思考(拓展思维)谈谈你的收获!!1.一般地,对于形如x2=a(a≥0)的方程,根据平方根的定义,可解得
这种解一元二次方程的方法叫做开平方法.2.把一元二次方程的左边配成一个完全平方式,然后用开平方法求解,这种解一元二次方程的方法叫做配方法. 注意:配方时, 等式两边同时加上的是一次项
系数一半的平方.用配方法解一元二次方程的步骤:移项:把常数项移到方程的右边;
配方:方程两边都加上一次项系数一半的平方;
开方:根据平方根意义,方程两边开平方;
求解:解一元一次方程;
定解:写出原方程的解.训案(见WORD)文档。
根据平方根的定义,可解得
这种解一元二次方程的方法叫做开平方法.例1.用开平方法解下列方程:
(1)3x2-27=0;
(2)(2x-3)2=49
一元一次方程的根是唯一的,而一元二次方程的根却有两个。巩固练习 1(1)方程 的根是
(2)方程 的根是
(3) 方程 的根是 2. 选择适当的方法解下列方程:
(1)x2- 81=0 (2) x2 =50
(3)(x+1)2=4 (4)x2+2 x+5=0X1=0.5, x2=-0.5X1=3, x2=—3X1=2, x2=-1合作探究这种方程怎样解?变形为的形式.(a为非负常数)变形为X2-4x+1=0(x-2)2=3 把一元二次方程的左边配成一个完全平方式,然后用开平方法求解,这种解一元二次方程的方法叫做配方法.(1)x2+8x+ =(x+4)2
(2)x2-4x+ =(x- )2
(3)x2-___x+ 9 =(x- )2填空 配方时, 等式两边同时加上的是一次项系数一半的平方。166342。填空: 253656例2:用配方法解下列方程二次项系数为1二次项系数不为1可以先将系数化为1 ,移项,得 配方,得 由此可得 移项,得 配方得 由此可得 移项,得 二次项系数化为1,得 配方得 由此可得 移项,得 二次项系数化为1,得 配方得 用配方法解一元二次方程的步骤:移项:把常数项移到方程的右边;
系数化为1:将二次项系数化为1;
配方:方程两边都加上一次项系数一半的平方;
开方:根据平方根意义,方程两边开平方;
求解:解一元一次方程;
定解:写出原方程的解.练一练1(1)(2)(3)(4)练一练3(1)(2)(3)(4)(5)(6)练一练4(看谁快而准!)思考(拓展思维)谈谈你的收获!!1.一般地,对于形如x2=a(a≥0)的方程,根据平方根的定义,可解得
这种解一元二次方程的方法叫做开平方法.2.把一元二次方程的左边配成一个完全平方式,然后用开平方法求解,这种解一元二次方程的方法叫做配方法. 注意:配方时, 等式两边同时加上的是一次项
系数一半的平方.用配方法解一元二次方程的步骤:移项:把常数项移到方程的右边;
配方:方程两边都加上一次项系数一半的平方;
开方:根据平方根意义,方程两边开平方;
求解:解一元一次方程;
定解:写出原方程的解.训案(见WORD)文档。
同课章节目录
