一元二次方程应用1[上学期]
文档属性
| 名称 | 一元二次方程应用1[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 18.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-09-13 07:54:00 | ||
图片预览





文档简介
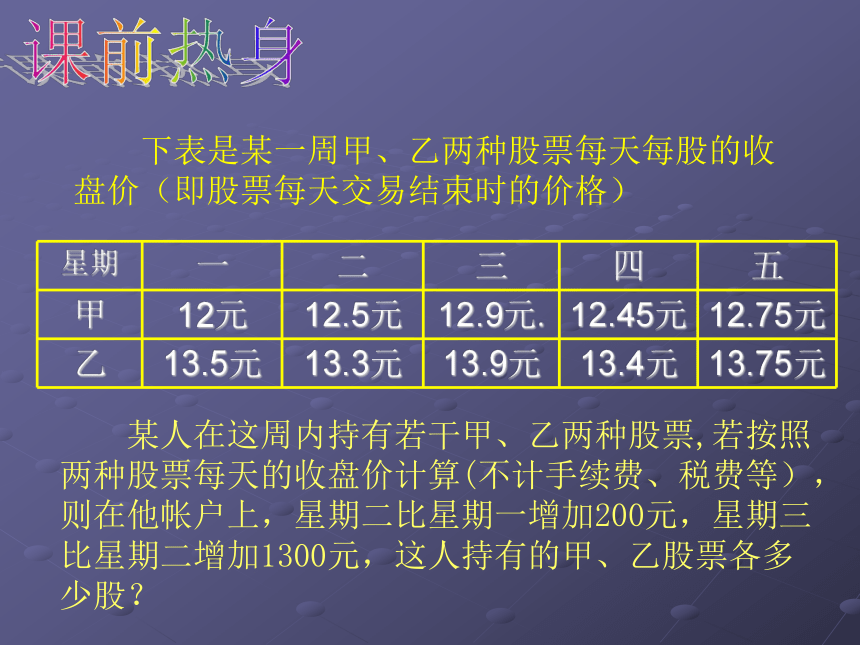
课件12张PPT。一元二次方程的应用(一) 下表是某一周甲、乙两种股票每天每股的收盘价(即股票每天交易结束时的价格) 某人在这周内持有若干甲、乙两种股票,若按照两种股票每天的收盘价计算(不计手续费、税费等),则在他帐户上,星期二比星期一增加200元,星期三比星期二增加1300元,这人持有的甲、乙股票各多少股?课前热身 回顾列方程解应用题的一般步骤:(1)弄清题意和题目中的数量关系, 设字母表示题目中的一个未知数;
(2)找出能够表示应用题全部含义的一个相等关系;
(3)根据所找到的相等关系列出需要的代数式,从而列出方程;
(4)解所得到的方程,求出未知数的值;
(5)检验所求出的解,看它是否符合题意以确定问题的答案;
(6)写出答案(包括单位和名称)
列方程解应用题的一般步骤探索新知活动一 有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人? 有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人? 这个问题涉及到了哪几个量? 所涉及的量是:传染源人数、被传染的人数、一共患流感的人数。 分析:设每轮传染中平均一个人传染了x个人。开始有一个人患了流感,第一轮的传染源就是这个人,他传染了x个人。用代数式表示,第一轮后共有 人患了流感;第二轮传染中,这些人中的每个人又传染了x个人,用代数式表示,第二轮后共有 人患了流感。(1+x)[1+x+x(1+x)]用表格表示为:活动二 某工厂第一季度的一月份生产电视机是1万台,第一季度生产电视机的总台数是3.31万台,求二月份、三月份生产电视机平均增长的百分率是多少? 分析:设二、三月份生产电视机平均增长的百分率为x万元.
因为一月份是1万台,那么二月份应是 台,三月份应在二月份的 的基础上增加相同的倍数( )即为 .(1+x)(1+x)(1+x)(1+x)2活动三 某人将2000元人民币按一年定期存入银行,到期后支取1000元用于购物,剩下1000元及应得利息又全部按一年定期存入银行,若存款的利率不变,到期后本金和利息共1320元,求这种存款方式的年利率。 分析:设这种存款方式的年利率为x,第一次存2000元取1000元,剩下的本金各利息是(1000+2000x.80%);第二次存,本金就变为(1000+2000x.80%),其它的依此类推。活动四 两年前生产1吨甲种药品的成本是5000元,生产1吨乙种药品的成本是6000元,随着生产技术的进步,现在生产1吨甲种药品的成本是3000元,生产1吨乙种药品的成本是3600元,哪能种药品成本的年平均下降率较大?巩固练习 1.某林场现有木材a 立方米,预计在今后两年内年平均增长p%,那么两年后该林场有木材多少立方米? 2.某化工厂今年一月份生产化工原料15万吨,通过优化管理,产量逐年上升,第一季度共生产化工原料60万吨,设二、三月份平均增长的百分率相同,均为x,可列出方程为 . 这节课你学到了什么,你有什么新的感受?作业:p53 复习巩固1 综合运用4
(2)找出能够表示应用题全部含义的一个相等关系;
(3)根据所找到的相等关系列出需要的代数式,从而列出方程;
(4)解所得到的方程,求出未知数的值;
(5)检验所求出的解,看它是否符合题意以确定问题的答案;
(6)写出答案(包括单位和名称)
列方程解应用题的一般步骤探索新知活动一 有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人? 有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人? 这个问题涉及到了哪几个量? 所涉及的量是:传染源人数、被传染的人数、一共患流感的人数。 分析:设每轮传染中平均一个人传染了x个人。开始有一个人患了流感,第一轮的传染源就是这个人,他传染了x个人。用代数式表示,第一轮后共有 人患了流感;第二轮传染中,这些人中的每个人又传染了x个人,用代数式表示,第二轮后共有 人患了流感。(1+x)[1+x+x(1+x)]用表格表示为:活动二 某工厂第一季度的一月份生产电视机是1万台,第一季度生产电视机的总台数是3.31万台,求二月份、三月份生产电视机平均增长的百分率是多少? 分析:设二、三月份生产电视机平均增长的百分率为x万元.
因为一月份是1万台,那么二月份应是 台,三月份应在二月份的 的基础上增加相同的倍数( )即为 .(1+x)(1+x)(1+x)(1+x)2活动三 某人将2000元人民币按一年定期存入银行,到期后支取1000元用于购物,剩下1000元及应得利息又全部按一年定期存入银行,若存款的利率不变,到期后本金和利息共1320元,求这种存款方式的年利率。 分析:设这种存款方式的年利率为x,第一次存2000元取1000元,剩下的本金各利息是(1000+2000x.80%);第二次存,本金就变为(1000+2000x.80%),其它的依此类推。活动四 两年前生产1吨甲种药品的成本是5000元,生产1吨乙种药品的成本是6000元,随着生产技术的进步,现在生产1吨甲种药品的成本是3000元,生产1吨乙种药品的成本是3600元,哪能种药品成本的年平均下降率较大?巩固练习 1.某林场现有木材a 立方米,预计在今后两年内年平均增长p%,那么两年后该林场有木材多少立方米? 2.某化工厂今年一月份生产化工原料15万吨,通过优化管理,产量逐年上升,第一季度共生产化工原料60万吨,设二、三月份平均增长的百分率相同,均为x,可列出方程为 . 这节课你学到了什么,你有什么新的感受?作业:p53 复习巩固1 综合运用4
同课章节目录
