湖南省2013年数学参赛课件:函数的基本性质(人教版必修一第一章第三节)
文档属性
| 名称 | 湖南省2013年数学参赛课件:函数的基本性质(人教版必修一第一章第三节) |

|
|
| 格式 | zip | ||
| 文件大小 | 1013.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-11-27 00:00:00 | ||
图片预览


文档简介
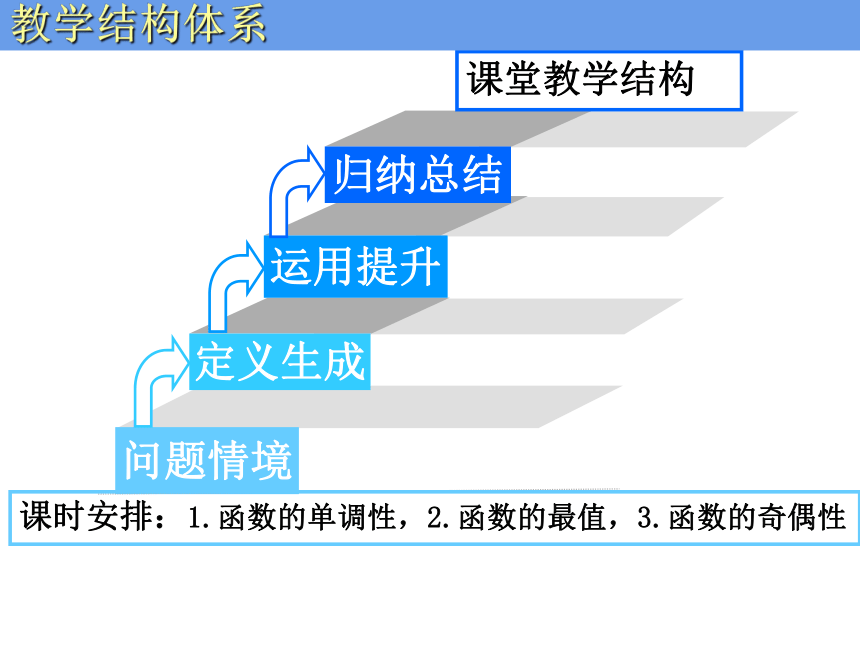
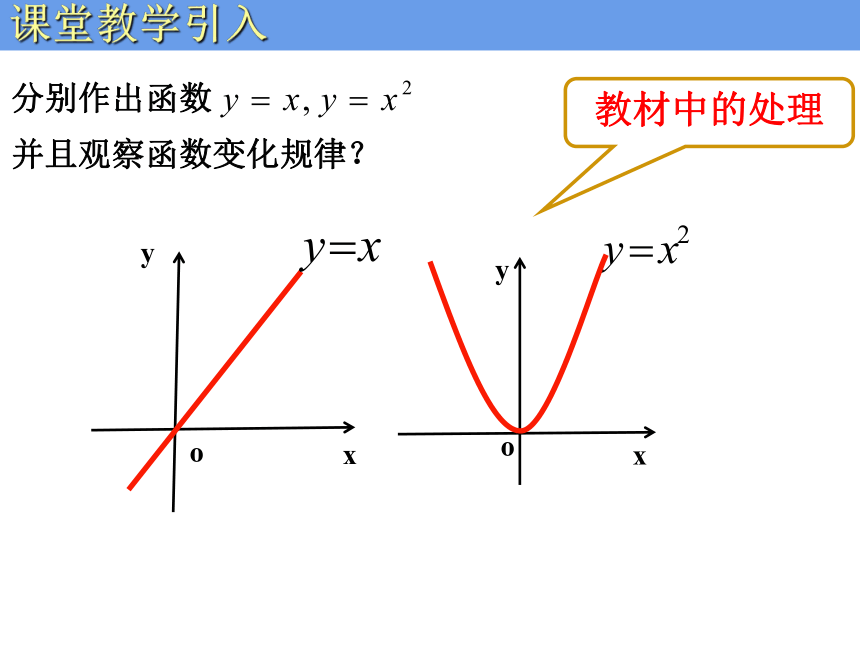
课件27张PPT。郴州市三中 宋艳林 函数的基本性质人教版高中数学必修一第一章1.3节教学结构体系1课堂教学引入2《函数的基本性质》---教学资源运用与设计课堂教学引入2《函数的基本性质》---教学资源运用与设计函数的基本性质教学结构体系课时安排:1.函数的单调性,2.函数的最值,3.函数的奇偶性课堂教学结构教学结构体系《函数的基本性质》---教学资源运用与设计xyo分别作出函数 的图象,
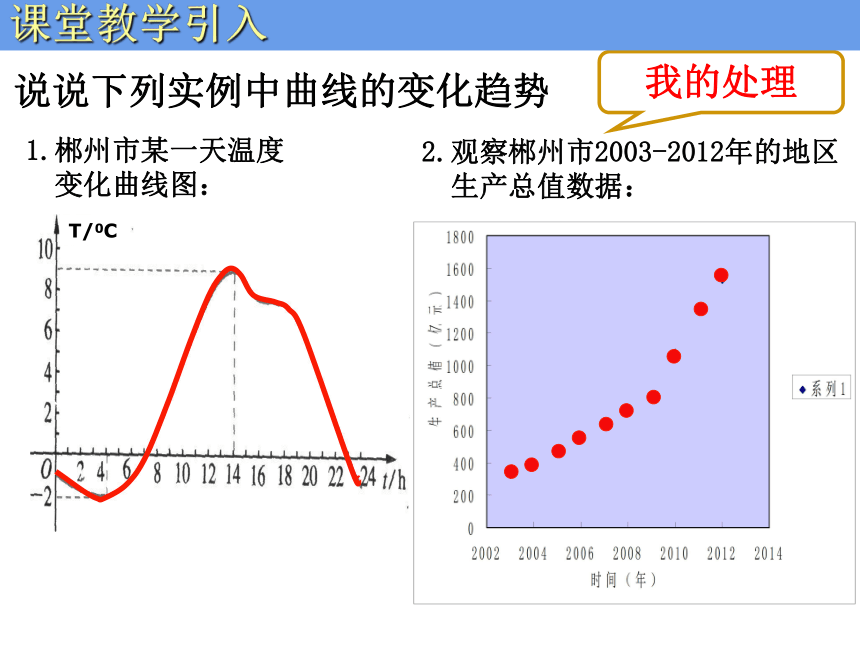
并且观察函数变化规律? 教材中的处理课堂教学引入下楼梯上楼梯观察下列视频中,每走一步李辉同学的相应位置有何变化?课堂教学引入我的处理说说下列实例中曲线的变化趋势1.郴州市某一天温度
变化曲线图:我的处理2.观察郴州市2003-2012年的地区
生产总值数据:T/0C课堂教学引入《函数的基本性质》---教学资源运用与设计函数单调性的定义:学情分析直观感知(小学):如“从左往右看,图象越来越高”形象描述(初中):如“y随着x的增大而增大”。抽象概念(高中):定义生成探究:你能用自己的方式刻画函数f(x)=x 中x、f(x)的变化趋势吗?特值对比能反映整体趋势吗?合作探究定义生成 ── 突出教学重点直观形象清晰自我表述结果展示交流评价质疑修正重点突出---合作探究、动画展示定义生成12f(1)f(2)x2x1x2x1f(x1)f(x2)f(x1)f(x2)12f(1)f(2)xyyxoo(图一)(图二)由形到数由数到形重点突出---合作探究、动画展示定义生成探究:你能用自己的方式刻画函数f(x)=x 中x、f(x)的变化趋势吗?特值对比能反映整体趋势吗?合作探究定义生成 ── 突出教学重点… x1如何用定义证明函数 在 上为增函数?难点突破---2 .遵循认知规律设计问题遵循认知规律设计问题 ── 突出教学难点问题导学问题1. 你能用定义具体描述f(x)的单调性吗?问题2. 利用定义证明f(x)的函调性关键点在何处?问题3. 比较f(x1)、f(x2)大小难点在哪?如何突破?问题4. 你能写出证明过程吗?导出证明框架指出证明关键实践提炼方法强化证明过程与步骤探究:
如何用定义证明函数 在 上为增函数?难点突破---2 .遵循认知规律设计问题归纳总结: 1.证明函数单调性的有哪些关键步骤?
2.我的学习心得体会有哪些?
3.哪些地方还需提升? 教材例题难点突破---2 .遵循认知规律设计问题改编使用课本例题── 贴近本校学情探究(教材P30页) :画出反比例函数 y= 的图象。①这个函数的定义域是什么?
②在这个函数的定义域上的单调性是什么? 学情分析方法处理很多学生会理解为f(x)在定义域内为减函数,
源于学生对函数单调性的本质理解不到位。按认知规律设计问题,深化概念理解。难点突破---2 .遵循认知规律设计问题xOyx1x2f(x1)f(x2)问题1探究(教材P30页) :画出反比例函数 y= 的图象。
U
,难点突破---2 .遵循认知规律设计问题yOx形:从左——右,整体上升 数:取值——任意性,变化——一致性改编使用课本例题── 贴近本校学情如图,函数f(x)在 上都是增函数,
何时f(x)在R上也是增函数?问题2yOxx1x2难点突破---2 .遵循认知规律设计问题 1.如图是定义在闭区间[-5,6]上的函数f(x)的
图象,根据图象说出f(x)的单调区间,以及在每
一区间上,f(x) 是增函数还是减函数. 难点突破---3 .按照掌握层次设计问题
生活现象:在一碗水中加入一定量的糖,糖加的越多糖水越甜(糖水不饱和状态下)。你能用本堂课所学知识解释这一生活现象吗?课堂教学引入2《函数的基本性质》---教学资源运用与设计资源运用与教学设计评价教 材多媒体软件生活
实例分组学习与合作探究相结合按梯度分层次设计问题导学数形结合、特殊到一般、类比等思想爱与兴趣比知识本身更重要郴州欢迎您!
并且观察函数变化规律? 教材中的处理课堂教学引入下楼梯上楼梯观察下列视频中,每走一步李辉同学的相应位置有何变化?课堂教学引入我的处理说说下列实例中曲线的变化趋势1.郴州市某一天温度
变化曲线图:我的处理2.观察郴州市2003-2012年的地区
生产总值数据:T/0C课堂教学引入《函数的基本性质》---教学资源运用与设计函数单调性的定义:学情分析直观感知(小学):如“从左往右看,图象越来越高”形象描述(初中):如“y随着x的增大而增大”。抽象概念(高中):定义生成探究:你能用自己的方式刻画函数f(x)=x 中x、f(x)的变化趋势吗?特值对比能反映整体趋势吗?合作探究定义生成 ── 突出教学重点直观形象清晰自我表述结果展示交流评价质疑修正重点突出---合作探究、动画展示定义生成12f(1)f(2)x2x1x2x1f(x1)f(x2)f(x1)f(x2)12f(1)f(2)xyyxoo(图一)(图二)由形到数由数到形重点突出---合作探究、动画展示定义生成探究:你能用自己的方式刻画函数f(x)=x 中x、f(x)的变化趋势吗?特值对比能反映整体趋势吗?合作探究定义生成 ── 突出教学重点… x1
如何用定义证明函数 在 上为增函数?难点突破---2 .遵循认知规律设计问题归纳总结: 1.证明函数单调性的有哪些关键步骤?
2.我的学习心得体会有哪些?
3.哪些地方还需提升? 教材例题难点突破---2 .遵循认知规律设计问题改编使用课本例题── 贴近本校学情探究(教材P30页) :画出反比例函数 y= 的图象。①这个函数的定义域是什么?
②在这个函数的定义域上的单调性是什么? 学情分析方法处理很多学生会理解为f(x)在定义域内为减函数,
源于学生对函数单调性的本质理解不到位。按认知规律设计问题,深化概念理解。难点突破---2 .遵循认知规律设计问题xOyx1x2f(x1)f(x2)问题1探究(教材P30页) :画出反比例函数 y= 的图象。
U
,难点突破---2 .遵循认知规律设计问题yOx形:从左——右,整体上升 数:取值——任意性,变化——一致性改编使用课本例题── 贴近本校学情如图,函数f(x)在 上都是增函数,
何时f(x)在R上也是增函数?问题2yOxx1x2难点突破---2 .遵循认知规律设计问题 1.如图是定义在闭区间[-5,6]上的函数f(x)的
图象,根据图象说出f(x)的单调区间,以及在每
一区间上,f(x) 是增函数还是减函数. 难点突破---3 .按照掌握层次设计问题
生活现象:在一碗水中加入一定量的糖,糖加的越多糖水越甜(糖水不饱和状态下)。你能用本堂课所学知识解释这一生活现象吗?课堂教学引入2《函数的基本性质》---教学资源运用与设计资源运用与教学设计评价教 材多媒体软件生活
实例分组学习与合作探究相结合按梯度分层次设计问题导学数形结合、特殊到一般、类比等思想爱与兴趣比知识本身更重要郴州欢迎您!
