一元二次方程[上学期]

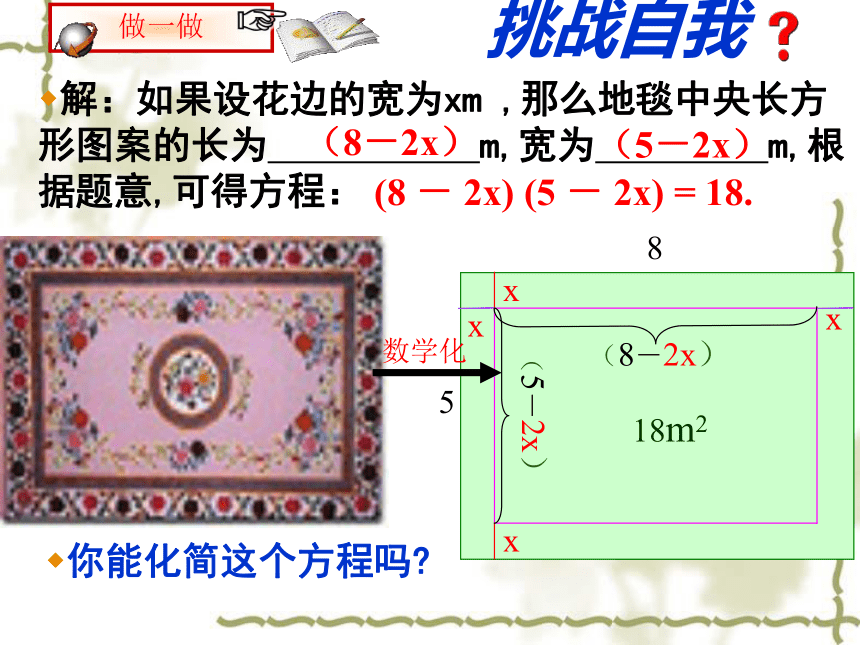
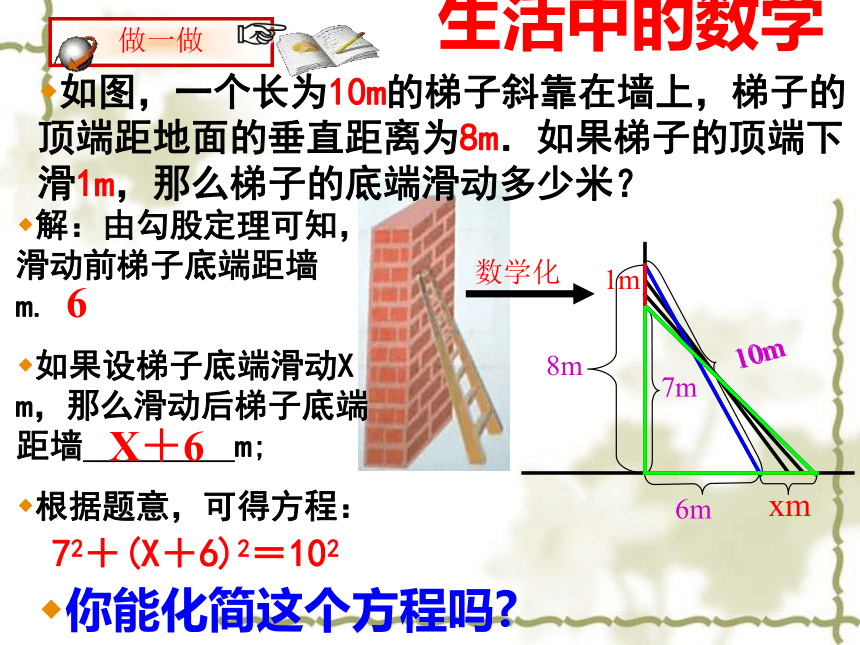
课件15张PPT。一元二次方程花边有多宽一块四周镶有宽度相等的花边的地毯如下图，它的长为８m，宽为５m．如果地毯中央长方形图案的面积为18m2 ，则花边有多宽?你怎么解决这个问题？挑战自我解：如果设花边的宽为xm ,那么地毯中央长方形图案的长为 m,宽为　　　 m,根据题意,可得方程：你能化简这个方程吗? （8－2x）（5－2x） (8 － 2x) (5 － 2x) = 18.5xxxx （8－2x）（5－2x）818m2生活中的数学如图，一个长为10m的梯子斜靠在墙上，梯子的顶端距地面的垂直距离为8m．如果梯子的顶端下滑1m，那么梯子的底端滑动多少米？解：由勾股定理可知，滑动前梯子底端距墙　　　　m.
如果设梯子底端滑动X m，那么滑动后梯子底端距墙　　 m;
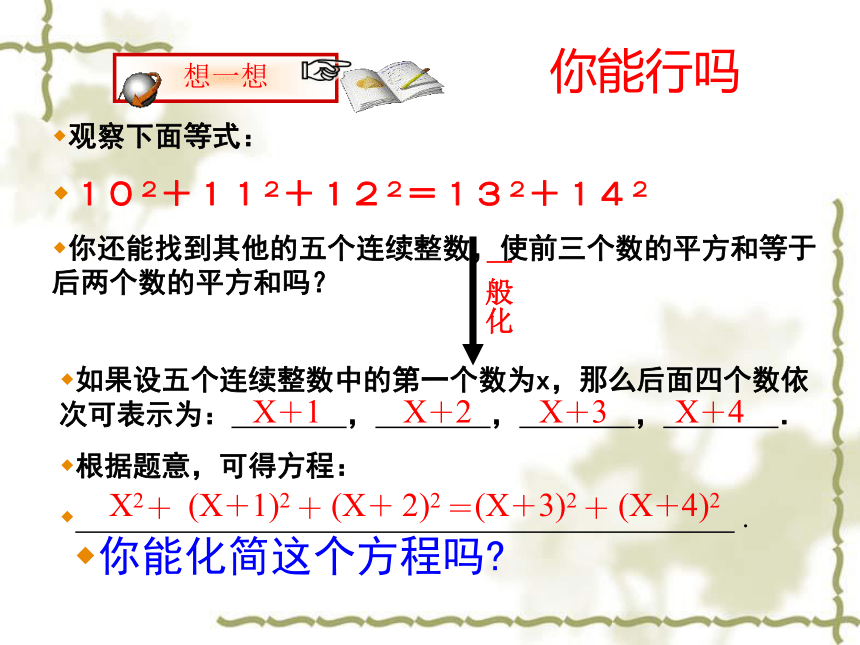
根据题意，可得方程：你能化简这个方程吗?6X＋672＋(X＋6)2＝102xm8m10m7m6m10m1m你能行吗观察下面等式：
１０２＋１１２＋１２２＝１３２＋１４２
你还能找到其他的五个连续整数，使前三个数的平方和等于后两个数的平方和吗？如果设五个连续整数中的第一个数为x，那么后面四个数依次可表示为：　　　　，　　　　，　　　　，　　　　．你能化简这个方程吗?X＋1X＋2X＋3X＋4根据题意，可得方程：
　　　　　　　　　　　　 . 上面的方程都是只含有　　　　　　的　　　　 ，并且都可以化为　　　　　　　　　　　　　　　　　 的形式，这样的方程叫做一元二次方程．一元二次方程的概念由上面三个问题，我们可以得到三个方程：把ax２＋bx＋c＝０(a，b，c为常数,a≠０)称为一元二次方程的一般形式，其中ax２ ， bx ， c分别称为二次项、一次项和常数项，a， b分别称为二次项系数和一次项系数．(8-2x)(５-２x)=18;即 2x2 － 13x ＋ 11 = 0 .x２+x+1)２+(x+2)２=(x+3)２+(x+４)２即 x2 － 8x － 20＝0.（ x＋６）２＋７２＝１０２即 x2 ＋12 x －15 ＝0.上述三个方程有什么共同特点？一个未知数x整式方程ax２＋bx＋c＝０(a，b，c为常数, a≠０)做一做:判断下列方程是否为一元二次方程.(1)X2+X=36(2)X3+X2=36(3)X2+3Y=36(5)X2=X(X+1)+36(6)ax2+bx+c=0(a≠0)　试试看：若关于x的方程(m-1)x2+3x-4=0是一元二
次方程, 则m的取值范围是______.例1:
将方程3x(x-1)=5(x+2)化成一元二次方程的一般形式,并写出它的二次项系数,一次项系数和常数项.3x2-8x-10=0该注意点什么？合作探究巩固提高-4
2x2-x-4=02
-1-4y2+2y=0-4
2
0
3x2-2x-1=0
3-2
-1
1.下列是一元二次方程的是（ ）
A. X2+3x-2 B. x2+3x-2=x2
C. X2=2+3x D. x2-x3+4=04.若关于x的方程kx2+x=2x2+1是一元二次方程，则
k的取值范围是_____.2.写出一个一元二次方程，使它的各项系数之和为 6，
则方程可以是______. 3.关于x的一元二次方程(m-3)x2-(m-1)x-m=0的二次项
系数是_____,一次项系数是_____,常数项是_____. 做一做,看看你学会了吗?根据下列问题，列出关于x的方程，并将其化成一般形式。1. 4个完全相同的正方形的面积之和为25，
求正方形的边长x。2.一个直角三角形的斜边长为10，两条直角边
相差2，求较长的直角边长x。3.参加一次聚会的每两个人都握了一次手，所
有人共握10次，求参加聚会的人数x.关于x的方程(m2-9)x2+(m+3)x+5m-1=0，

(1)当m取何值时是一元二次方程？

(2)当m取何值时是一元一次方程？ 关于X的方程(2m2+3)x2+5x=13
一定是一元二次方程吗？为什么?★★思考题： 回味无穷本节课你又学会了哪些新知识呢？
１．学习了什么是一元二次方程，以及它的一般形式ax２＋bx＋c＝０（a，b，c为常数，a≠０）和有关概念，如二次项、一次项、常数项、二次项系数、一次项系数．
２．会用一元二次方程表示实际生活中的数量关系
你准备如何去求方程中的未知数呢?结束寄语运用方程（方程组）解答相关的实际问题是一种重要的数学思想——方程的思想.
一元二次方程也是刻画现实世界的有效数学模型.