北师大版五年级上册数学6.1 组合图形的面积 课时精练(含答案)
文档属性
| 名称 | 北师大版五年级上册数学6.1 组合图形的面积 课时精练(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 159.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-05 00:00:00 | ||
图片预览

文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
北师大版五年级上册数学组合图形的面积课时精练(附答案)
一、单选题
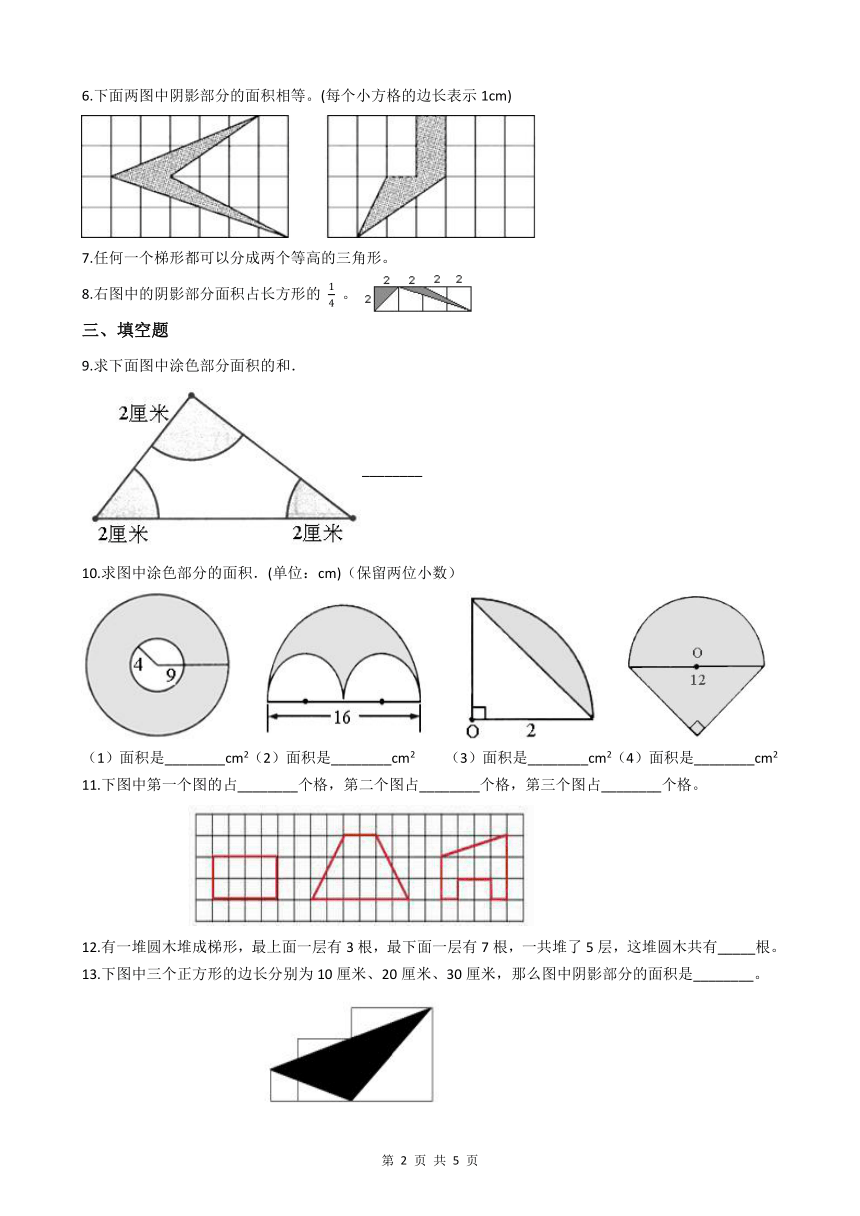
1.下面每个小正方形的面积是1平方厘米,面积不是6平方厘米的四边形是( )。
A. B. C. D.
2.观察图,下列选项正确的是( )。
A. 甲周长<乙周长 B. 甲面积=乙面积 C. 甲周长=乙周长 D. 甲面积>乙面积
3.一个长方体被挖一小块(如图),下面说法完全正确的是( )
A. 体积减少,表面积不变 B. 体积减少,表面积减少 C. 体积不变,表面积不变
4.下图是由一个大正方形与一个小正方形拼成的,已知小正方形的边长为4cm,阴影部分的面积为28cm2。那么空白部分的面积为( )cm2。
A. 20 B. 24 C. 28 D. 32
5.如图,想知道这片叶子的面积,可以用方格纸估计。用下面( )种规格的方格纸估计,能更接近实际面积。
A. B. C.
二、判断题
6.下面两图中阴影部分的面积相等。(每个小方格的边长表示1cm)
7.任何一个梯形都可以分成两个等高的三角形。
8.右图中的阴影部分面积占长方形的 。
三、填空题
9.求下面图中涂色部分面积的和.
________
10.求图中涂色部分的面积.(单位:cm)(保留两位小数)
(1)面积是________cm2(2)面积是________cm2 (3)面积是________cm2(4)面积是________cm2
11.下图中第一个图的占________个格,第二个图占________个格,第三个图占________个格。
12.有一堆圆木堆成梯形,最上面一层有3根,最下面一层有7根,一共堆了5层,这堆圆木共有_____根。
13.下图中三个正方形的边长分别为10厘米、20厘米、30厘米,那么图中阴影部分的面积是________。
四、计算题
14.直角梯形的上底、下底分别是2厘米、6厘米,两条腰分别是3厘米、5厘米,图中阴影部分的面积是多少平方厘米?(看图计算)
15.计算下面图形的周长和面积。
(1) (2)
五、解答题
16.计算下面图形的周长和面积。
(1) (2)
17.这块木板有多重
六、综合题
18.图形计算
已知ABCD和CEFG都是正方形,且正方形ABCD的边长为10厘米.则图中阴影部分(三角形BFD)的面积是多少?
提示:本题没有限制CEFG的边长,说明它的边长长度可变,不确定.我们不妨假设CEFG变成和ABCD同样大或变成很小,即忽略成一个点这两种情况来解答.
(1)请你按提示画出这两种特殊情况的示意图,用阴影表示出要求的面积,并解答
(2)根据提示和计算结果,你能得出一个什么结论?
答案
一、单选题
1. C 2. C 3. A 4. B 5. A
二、判断题
6. 正确 7. 正确 8. 正确
三、填空题
9. 6.28平方厘米 10. (1)204.1(2)50.24(3)1.14(4)74.52
11. 8;12;8 12. 25 13. 600平方厘米
四、计算题
14. 解: ×3×1.5=2.25(平方厘米)
答:图中阴影部分的面积是2.25平方厘米
15. (1)周长:(8+10)×2=36(厘米)
面积:10×8-5×7=80-35=45(平方厘米)
(2)周长:(12+8)×2+3×2=46(分米)
面积:8×12-3×4=84(平方分米)
五、解答题
16. (1)解:64×4=256(米)
64×64=4096(平方米)
答:正方形的周长是256米,面积是4096平方米。
(2)解:(36+24)×2+6×2=120+12=132(米)
36×24-12×6 =864-72 =792(平方米)
答:图形的周长是132米,面积是792平方米。
17. 解:[(6.2+10)×12.5÷2-6.4×10.5÷2]×0.4=(16.2×12.5÷2-33.6)×0.4=(101.25-33.6)×0.4=67.65×0.4=27.06(千克)
答:这块木板有27.06千克。
六、综合题
18. (1)解:①假设CEFG变成和ABCD同样大,
;
所以三角形BFD的面积是:
10×10÷2,=100÷2,=50(平方厘米).
②假设是一个点,则如图所示:
.
三角形BFD的面积是:10×10÷2=50(平方厘米).
答:三角形BFD的面积是50平方厘米.
(2)解:发现考虑到两个极端时,阴影部分的面积都一样大
(
第
1
页 共
7
页
)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
北师大版五年级上册数学组合图形的面积课时精练(附答案)
一、单选题
1.下面每个小正方形的面积是1平方厘米,面积不是6平方厘米的四边形是( )。
A. B. C. D.
2.观察图,下列选项正确的是( )。
A. 甲周长<乙周长 B. 甲面积=乙面积 C. 甲周长=乙周长 D. 甲面积>乙面积
3.一个长方体被挖一小块(如图),下面说法完全正确的是( )
A. 体积减少,表面积不变 B. 体积减少,表面积减少 C. 体积不变,表面积不变
4.下图是由一个大正方形与一个小正方形拼成的,已知小正方形的边长为4cm,阴影部分的面积为28cm2。那么空白部分的面积为( )cm2。
A. 20 B. 24 C. 28 D. 32
5.如图,想知道这片叶子的面积,可以用方格纸估计。用下面( )种规格的方格纸估计,能更接近实际面积。
A. B. C.
二、判断题
6.下面两图中阴影部分的面积相等。(每个小方格的边长表示1cm)
7.任何一个梯形都可以分成两个等高的三角形。
8.右图中的阴影部分面积占长方形的 。
三、填空题
9.求下面图中涂色部分面积的和.
________
10.求图中涂色部分的面积.(单位:cm)(保留两位小数)
(1)面积是________cm2(2)面积是________cm2 (3)面积是________cm2(4)面积是________cm2
11.下图中第一个图的占________个格,第二个图占________个格,第三个图占________个格。
12.有一堆圆木堆成梯形,最上面一层有3根,最下面一层有7根,一共堆了5层,这堆圆木共有_____根。
13.下图中三个正方形的边长分别为10厘米、20厘米、30厘米,那么图中阴影部分的面积是________。
四、计算题
14.直角梯形的上底、下底分别是2厘米、6厘米,两条腰分别是3厘米、5厘米,图中阴影部分的面积是多少平方厘米?(看图计算)
15.计算下面图形的周长和面积。
(1) (2)
五、解答题
16.计算下面图形的周长和面积。
(1) (2)
17.这块木板有多重
六、综合题
18.图形计算
已知ABCD和CEFG都是正方形,且正方形ABCD的边长为10厘米.则图中阴影部分(三角形BFD)的面积是多少?
提示:本题没有限制CEFG的边长,说明它的边长长度可变,不确定.我们不妨假设CEFG变成和ABCD同样大或变成很小,即忽略成一个点这两种情况来解答.
(1)请你按提示画出这两种特殊情况的示意图,用阴影表示出要求的面积,并解答
(2)根据提示和计算结果,你能得出一个什么结论?
答案
一、单选题
1. C 2. C 3. A 4. B 5. A
二、判断题
6. 正确 7. 正确 8. 正确
三、填空题
9. 6.28平方厘米 10. (1)204.1(2)50.24(3)1.14(4)74.52
11. 8;12;8 12. 25 13. 600平方厘米
四、计算题
14. 解: ×3×1.5=2.25(平方厘米)
答:图中阴影部分的面积是2.25平方厘米
15. (1)周长:(8+10)×2=36(厘米)
面积:10×8-5×7=80-35=45(平方厘米)
(2)周长:(12+8)×2+3×2=46(分米)
面积:8×12-3×4=84(平方分米)
五、解答题
16. (1)解:64×4=256(米)
64×64=4096(平方米)
答:正方形的周长是256米,面积是4096平方米。
(2)解:(36+24)×2+6×2=120+12=132(米)
36×24-12×6 =864-72 =792(平方米)
答:图形的周长是132米,面积是792平方米。
17. 解:[(6.2+10)×12.5÷2-6.4×10.5÷2]×0.4=(16.2×12.5÷2-33.6)×0.4=(101.25-33.6)×0.4=67.65×0.4=27.06(千克)
答:这块木板有27.06千克。
六、综合题
18. (1)解:①假设CEFG变成和ABCD同样大,
;
所以三角形BFD的面积是:
10×10÷2,=100÷2,=50(平方厘米).
②假设是一个点,则如图所示:
.
三角形BFD的面积是:10×10÷2=50(平方厘米).
答:三角形BFD的面积是50平方厘米.
(2)解:发现考虑到两个极端时,阴影部分的面积都一样大
(
第
1
页 共
7
页
)
同课章节目录
- 一 小数除法
- 1 精打细算
- 2 打扫卫生
- 3 谁打电话的时间长
- 4 人民币兑换
- 5 除得尽吗
- 6 调查“生活垃圾”
- 二 轴对称和平移
- 1 轴对称再认识(一)
- 2 轴对称再认识(二)
- 3 平移
- 4 欣赏与设计
- 三 倍数与因数
- 1 倍数与因数
- 2 探索活动:2、5的倍数的特征
- 3 探索活动:3的倍数的特征
- 4 找因数
- 5 找质数
- 四 多边形的面积
- 1 比较图形的面积
- 2 认识底和高
- 3 探索活动:平行四边形的面积
- 4 探索活动:三角形的面积
- 5 探索活动:梯形的面积
- 五 分数的意义
- 1 分数的再认识(一)
- 2 分数的再认识(二)
- 3 分饼
- 4 分数与除法
- 5 分数基本性质
- 6 找最大的公因数
- 7 约分
- 8 找最小的公倍数
- 9 分数的大小
- 六 组合图形的面积
- 1 组合图形的面积
- 2 探索活动:成长的脚印
- 3 公顷、平方千米
- 数学好玩
- 1 设计秋游方案
- 2 图形中的规律
- 3 尝试与猜测
- 七 可能性
- 1 谁先走
- 2 摸球游戏
