一元二次方程的根的判别式[上学期]
文档属性
| 名称 | 一元二次方程的根的判别式[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 79.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-09-07 00:00:00 | ||
图片预览




文档简介
课件10张PPT。一元二次方程判别式课件制作
主 讲余小芳一元二次方程判别式一复习提问:
1、一元二次方程的标准式是什么?
2、一元二次方程的求根公式是什么?
想一想:b -4ac的符号与ax +bx+c=0会有关系吗?
做一做:用求根公式法解下列方程
(1)x -x-2=0 (2)x -6x+9=0 (3)x -x+1=0
看一看:上列三个方程的根与b -4ac的符号有关系吗?有什么关系?222222一元二次方程判别式猜一猜:对于一般ax +bx+c=0 (a≠0)的根与b -4ac的符号有会么关系?22故对于方程ax +bx+c=0 (a≠0)有下列关系:
当b -4ac≥0时,方程有两个不相等的根
x =
当b-4ac=0时,方程有两个相等的根x =x = -
当b - 4ac<0时,方程没有实数根.因为ax +bx+c=0(a≠0)的求根公式是
-b±√b -4ac2ax=2222222-b+√b -4ac 2a21x =-b-√b -4ac2a2212b2a一元二次方程判别式反过来方程ax +bx+c=0有两个实数根时b -4ac>0
有两个相等的根时b -4ac=0
没有实数根时b -4ac<0
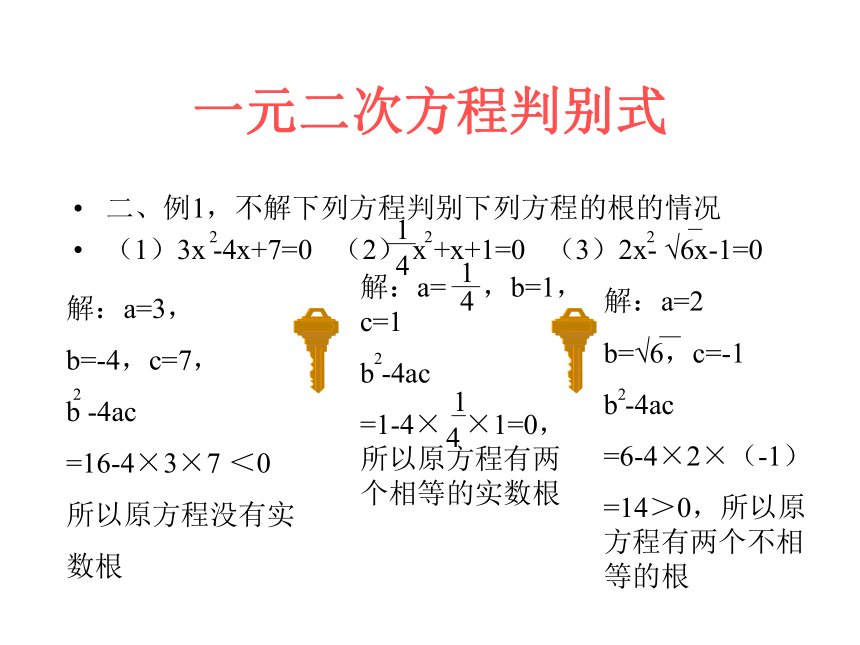
由此可见b -4ac的值决定一元二次方程的根的情况,所以把它叫一元二次方程ax +bx+c=0(a ≠0)的根的判别式。记作“△”读作“delta”222222二、例1,不解下列方程判别下列方程的根的情况
(1)3x -4x+7=0 (2) x +x+1=0 (3)2x- √6x-1=0一元二次方程判别式22214解:a=3,
b=-4,c=7,
b -4ac
=16-4×3×7 <0
所以原方程没有实
数根解:a= ,b=1,c=1
b -4ac
=1-4× ×1=0,所以原方程有两个相等的实数根414解:a=2
b=√6,c=-1
b -4ac
=6-4×2×(-1)
=14>0,所以原方程有两个不相等的根2221做练习:不解方程试判断下列方程的根的情况
(1)3x -7x+2=0 (2)9x +6x+1=0
(3)2x -(2+√2)x+3+√2=0
例2:关于x的方程2x +mx-2=2x-m,当m为何值时方程有两个相等的根?并求出它的根
一元二次方程判别式解;原方程可以整理成;2x +(m-2)x+m-2=0
a=2, b=m-2, c=-2+m ,b-4ac=(m-2)-4×2(-2+m)
据题意有m -12m+20=0∴m =2, m =10
当m=2时,x =x =0;当m=10时x =x =-222222221211222练习:当K为何值时方程(k-2)x +2kx-1=0有两个相等的实数根,并求出方程的根。
例3:当K为何值时,方程kx +(2k+1)x+k=0(k≠0)
(1)有两个不相等的根(2)有两个相等的根
(3)没有实数根一元二次方程判别式22解:∵b -4ac=(2k+1) -4k·k=4k+1,而方程有两个不相等的根∴4k+1≥0,即k≥-422若有两个相等根4k+1=0即k= -4若没有实数根则4k+1<0即k< -1411例4:求证:
(1)关于x的方程x +kx+k +1 =0没有实数根
(2)关于x的方程(x+a)(x-a)-x=2(x-1)总有两个不相等的根。一元二次方程判别式22(1)证明:∵△=b -4ac=k -4(k +1)= -3k -4无论k为何实数k ≥0∴△<0故原方程没有实数根。
22222(2)证明:整理原方程得 x -3x+2 -a =0
∵△=9-4×(2-a )=1+a 无论a为何值a ≥0
∴ △>0,故原方程有两个不相等的根22222课堂练习;
1、对于方程4(m+1)x +2(2m-1)x=1-m (m≠-1)
(1)方程有两个不相等的实数根,求m的取值范围
(2)方程有两个相等的实数根,求m的取值范围
(3)方程没有实数根,求m的取值范围
2、已知a+c≠0,a +b =c 求证(a+c)x +2bx+c-a=0总有相等的实数根
一元二次方程判别式22222一元二次方程判别式小结:方程ax +bx+c=0 (a≠0)
1、△=b -4ac叫一元二次方程的判别式
当△>0时方程有两个不相等的实数根
当△=0时方程有两个相等的实数根
△<0时方程无实数根
2、能灵活运用△讨论方程根的情况或知道根的情况,能正确运用△具备的条件解出待定系数的值
3、能正确运用△的符号证明方程何时有不相等的实数根,何时有相等的实数根,何时没有实数根的问题22
主 讲余小芳一元二次方程判别式一复习提问:
1、一元二次方程的标准式是什么?
2、一元二次方程的求根公式是什么?
想一想:b -4ac的符号与ax +bx+c=0会有关系吗?
做一做:用求根公式法解下列方程
(1)x -x-2=0 (2)x -6x+9=0 (3)x -x+1=0
看一看:上列三个方程的根与b -4ac的符号有关系吗?有什么关系?222222一元二次方程判别式猜一猜:对于一般ax +bx+c=0 (a≠0)的根与b -4ac的符号有会么关系?22故对于方程ax +bx+c=0 (a≠0)有下列关系:
当b -4ac≥0时,方程有两个不相等的根
x =
当b-4ac=0时,方程有两个相等的根x =x = -
当b - 4ac<0时,方程没有实数根.因为ax +bx+c=0(a≠0)的求根公式是
-b±√b -4ac2ax=2222222-b+√b -4ac 2a21x =-b-√b -4ac2a2212b2a一元二次方程判别式反过来方程ax +bx+c=0有两个实数根时b -4ac>0
有两个相等的根时b -4ac=0
没有实数根时b -4ac<0
由此可见b -4ac的值决定一元二次方程的根的情况,所以把它叫一元二次方程ax +bx+c=0(a ≠0)的根的判别式。记作“△”读作“delta”222222二、例1,不解下列方程判别下列方程的根的情况
(1)3x -4x+7=0 (2) x +x+1=0 (3)2x- √6x-1=0一元二次方程判别式22214解:a=3,
b=-4,c=7,
b -4ac
=16-4×3×7 <0
所以原方程没有实
数根解:a= ,b=1,c=1
b -4ac
=1-4× ×1=0,所以原方程有两个相等的实数根414解:a=2
b=√6,c=-1
b -4ac
=6-4×2×(-1)
=14>0,所以原方程有两个不相等的根2221做练习:不解方程试判断下列方程的根的情况
(1)3x -7x+2=0 (2)9x +6x+1=0
(3)2x -(2+√2)x+3+√2=0
例2:关于x的方程2x +mx-2=2x-m,当m为何值时方程有两个相等的根?并求出它的根
一元二次方程判别式解;原方程可以整理成;2x +(m-2)x+m-2=0
a=2, b=m-2, c=-2+m ,b-4ac=(m-2)-4×2(-2+m)
据题意有m -12m+20=0∴m =2, m =10
当m=2时,x =x =0;当m=10时x =x =-222222221211222练习:当K为何值时方程(k-2)x +2kx-1=0有两个相等的实数根,并求出方程的根。
例3:当K为何值时,方程kx +(2k+1)x+k=0(k≠0)
(1)有两个不相等的根(2)有两个相等的根
(3)没有实数根一元二次方程判别式22解:∵b -4ac=(2k+1) -4k·k=4k+1,而方程有两个不相等的根∴4k+1≥0,即k≥-422若有两个相等根4k+1=0即k= -4若没有实数根则4k+1<0即k< -1411例4:求证:
(1)关于x的方程x +kx+k +1 =0没有实数根
(2)关于x的方程(x+a)(x-a)-x=2(x-1)总有两个不相等的根。一元二次方程判别式22(1)证明:∵△=b -4ac=k -4(k +1)= -3k -4无论k为何实数k ≥0∴△<0故原方程没有实数根。
22222(2)证明:整理原方程得 x -3x+2 -a =0
∵△=9-4×(2-a )=1+a 无论a为何值a ≥0
∴ △>0,故原方程有两个不相等的根22222课堂练习;
1、对于方程4(m+1)x +2(2m-1)x=1-m (m≠-1)
(1)方程有两个不相等的实数根,求m的取值范围
(2)方程有两个相等的实数根,求m的取值范围
(3)方程没有实数根,求m的取值范围
2、已知a+c≠0,a +b =c 求证(a+c)x +2bx+c-a=0总有相等的实数根
一元二次方程判别式22222一元二次方程判别式小结:方程ax +bx+c=0 (a≠0)
1、△=b -4ac叫一元二次方程的判别式
当△>0时方程有两个不相等的实数根
当△=0时方程有两个相等的实数根
△<0时方程无实数根
2、能灵活运用△讨论方程根的情况或知道根的情况,能正确运用△具备的条件解出待定系数的值
3、能正确运用△的符号证明方程何时有不相等的实数根,何时有相等的实数根,何时没有实数根的问题22
同课章节目录
