冀教版数学八年级上册17.1等腰三角形(2)课件(共14张PPT)
文档属性
| 名称 | 冀教版数学八年级上册17.1等腰三角形(2)课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 235.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-05 00:00:00 | ||
图片预览




文档简介
(共14张PPT)
等腰三角形
第二课时
对于一个三角形,怎样判定它是不是等腰三角形呢
观察思考
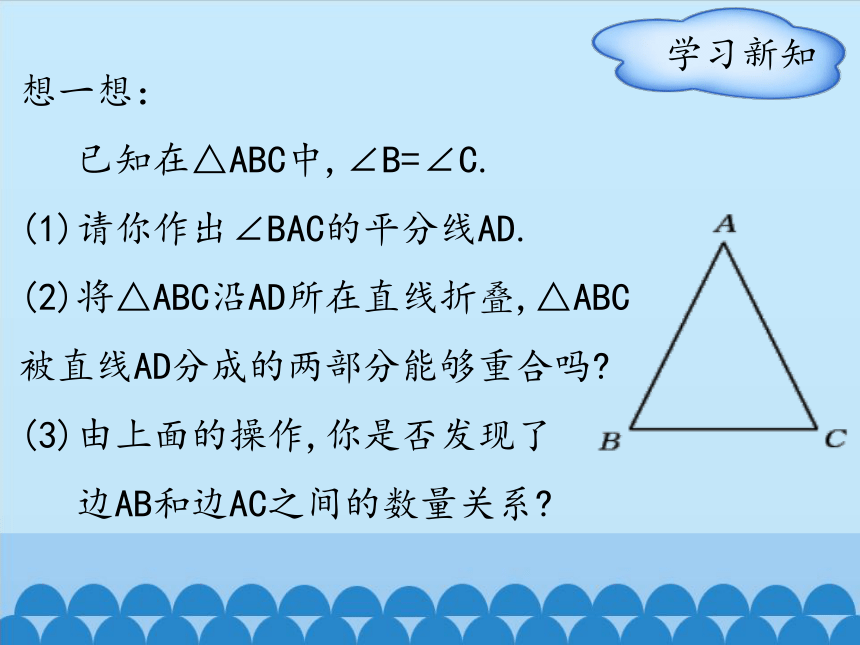
想一想:
已知在△ABC中,∠B=∠C.
(1)请你作出∠BAC的平分线AD.
(2)将△ABC沿AD所在直线折叠,△ABC
被直线AD分成的两部分能够重合吗
(3)由上面的操作,你是否发现了
边AB和边AC之间的数量关系
学习新知
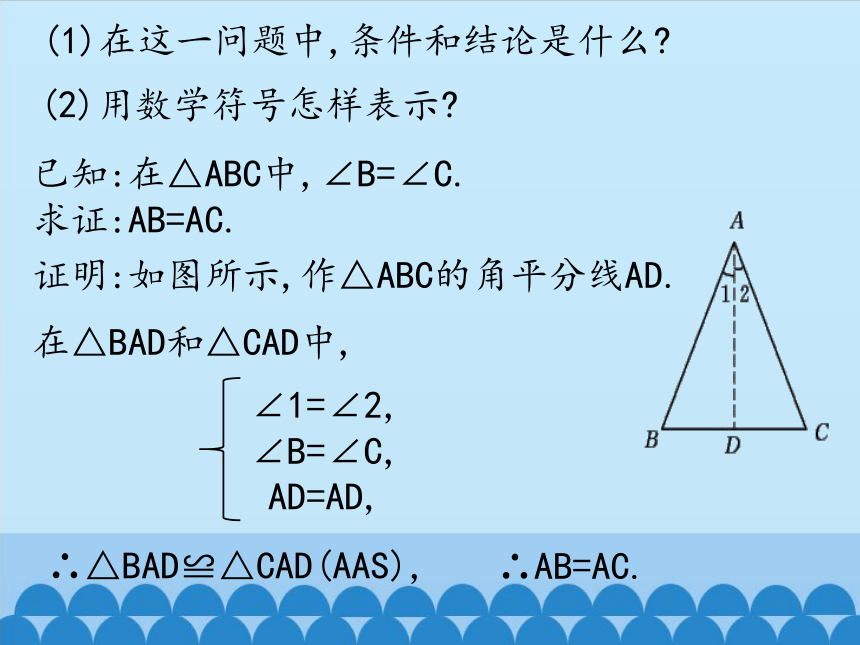
(1)在这一问题中,条件和结论是什么
已知:在△ABC中,∠B=∠C.
求证:AB=AC.
证明:如图所示,作△ABC的角平分线AD.
∠1=∠2,
∠B=∠C,
AD=AD,
在△BAD和△CAD中,
∴△BAD≌△CAD(AAS),
∴AB=AC.
(2)用数学符号怎样表示
归纳等腰三角形的判定方法:
如果一个三角形有两个角相等,那么这个三角形是等腰三角形,其中,两个相等的角所对的边也相等.简称“等角对等边”.
说明:三角形的“两边相等”和“两角相等”都是指在同一个三角形中才能得到“等边对等角”及“等角对等边”.“等边对等角”是性质,“等角对等边”是判定方法.
小结
如果一个三角形一边上的高、中线和这条边所对的角的平分线中有任意两条线段互相重合,那么这个三角形就是等腰三角形,这种方法是补充的一种方法,可以帮助我们解题时找思路,而在实际的解题过程中往往要转化为判定方法来解决.线段的垂直平分线的性质、角平分线的性质也可以判断相等,从而进一步说明三角形是等腰三角形.
知识拓展
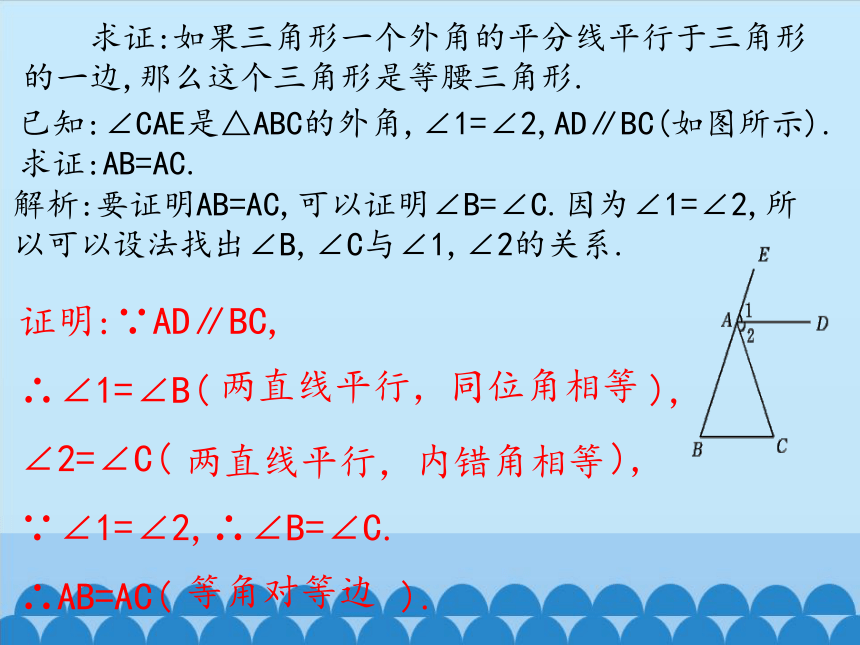
证明:∵AD∥BC,
∴∠1=∠B( ),
∠2=∠C( ),
∵∠1=∠2,∴∠B=∠C.
∴AB=AC( ).
求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
已知:∠CAE是△ABC的外角,∠1=∠2,AD∥BC(如图所示).
求证:AB=AC.
两直线平行,同位角相等
两直线平行,内错角相等
解析:要证明AB=AC,可以证明∠B=∠C.因为∠1=∠2,所以可以设法找出∠B,∠C与∠1,∠2的关系.
等角对等边
例:已知底边及底边上的高,用尺规作等腰三角形.如图所示,已知线段a和h.
求作等腰三角形ABC,使BC=a,高AD=h.
解:作法:
(1)作线段BC=a.
(2)作线段BC的垂直平分线MD,
垂足为点D.
(3)在DM上截取DA=h.
(4)连接AC,BC.
则△ABC就是所求作的等腰三角形.如图(2)所示.
图(2)
课堂小结
1.等腰三角形的判定定理:如果一个三角形有两个角相等,那么这个三角形是等腰三角形.其中,两个相等的角所对的边相等.(简称“等角对等边”)
说明:
(1)等腰三角形的判定定理与性质定理互逆;
(2)在判定定理的应用中,可以作底边上的高,也可以作顶角平分线,但不能作底边上的中线;
(3)判定定理在同一个三角形中才能适用.
2.等边三角形的判定定理
(1)三个角都相等的三角形是等边三角形.
(2)有一个角等于60°的等腰三角形是等边三角形.
检测反馈
1.如图所示,在△ABC中,AB=AC,点D,E在BC边
上, ∠ABD=∠DAE=∠EAC=36°,则图中等腰
三角形的个数是 ( )
A.4个 B.5个
C.6个 D.7个
C
解析:∵AB=AC,∠ABC=36°,∴∠ACB=36°,
∠BAC=108°,∵∠DAE=∠EAC=36°,
∴∠BAD=∠DAE=∠EAC=36°∴∠ADE=∠AED=72°,
∴△ABC, △ABD, △ADE, △ACE, △ACD, △ABE均是等腰三角形,共有6个.故选C.
2.如图所示,一艘海轮位于灯塔P的南偏东70°方向的M处,它以每小时40海里的速度向正北方向航行,2小时后到达位于灯塔P的北偏东40°的N处,则N与灯塔P的距离为( )
A.40海里 B.60海里
C.70海里 D.80海里
D
解析:MN=2×40=80(海里),由题意知∠M=70°,∠N=40°,
∴∠NPM=180°-∠M-∠N=180°- 70°- 40°=70°,
∴∠NPM=∠M,∴NP=MN=80海里.故选D.
3.如图所示,E是等边三角形ABC中AC边上的点,∠1=∠2,BE=CD,则△ADE的形状是( )
A.等腰三角形 B.等边三角形
C.不等腰三角形 D.不能确定形状
B
解析:∵△ABC为等边三角形,∴AB=AC.
∵∠1=∠2,BE=CD,∴△ABE≌△ACD,∴AE=AD,
∠BAE=∠CAD=60°,∴△ADE是等边三角形.故选B.
4.已知△ABC中,AB=AC,下列结论:
(1)若AB=BC,则△ABC是等边三角形;
(2)若∠A=60°,则△ABC是等边三角形;
(3)若∠B=60°,则△ABC是等边三角形.
其中正确的有 ( )
A.0个 B.1个 C.2个 D.3个
解析:因为AB=AC,AB=BC,所以AB=AC=BC,
所以△ABC是等边三角形,所以(1)正确;
因为AB=AC, ∠A=60°,所以△ABC是等边三角形,所以(2)正确;因为AB=AC∠B=60°,
所以△ABC是等边三角形,所以(3)正确.
正确的有3个.
D
谢 谢
等腰三角形
第二课时
对于一个三角形,怎样判定它是不是等腰三角形呢
观察思考
想一想:
已知在△ABC中,∠B=∠C.
(1)请你作出∠BAC的平分线AD.
(2)将△ABC沿AD所在直线折叠,△ABC
被直线AD分成的两部分能够重合吗
(3)由上面的操作,你是否发现了
边AB和边AC之间的数量关系
学习新知
(1)在这一问题中,条件和结论是什么
已知:在△ABC中,∠B=∠C.
求证:AB=AC.
证明:如图所示,作△ABC的角平分线AD.
∠1=∠2,
∠B=∠C,
AD=AD,
在△BAD和△CAD中,
∴△BAD≌△CAD(AAS),
∴AB=AC.
(2)用数学符号怎样表示
归纳等腰三角形的判定方法:
如果一个三角形有两个角相等,那么这个三角形是等腰三角形,其中,两个相等的角所对的边也相等.简称“等角对等边”.
说明:三角形的“两边相等”和“两角相等”都是指在同一个三角形中才能得到“等边对等角”及“等角对等边”.“等边对等角”是性质,“等角对等边”是判定方法.
小结
如果一个三角形一边上的高、中线和这条边所对的角的平分线中有任意两条线段互相重合,那么这个三角形就是等腰三角形,这种方法是补充的一种方法,可以帮助我们解题时找思路,而在实际的解题过程中往往要转化为判定方法来解决.线段的垂直平分线的性质、角平分线的性质也可以判断相等,从而进一步说明三角形是等腰三角形.
知识拓展
证明:∵AD∥BC,
∴∠1=∠B( ),
∠2=∠C( ),
∵∠1=∠2,∴∠B=∠C.
∴AB=AC( ).
求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
已知:∠CAE是△ABC的外角,∠1=∠2,AD∥BC(如图所示).
求证:AB=AC.
两直线平行,同位角相等
两直线平行,内错角相等
解析:要证明AB=AC,可以证明∠B=∠C.因为∠1=∠2,所以可以设法找出∠B,∠C与∠1,∠2的关系.
等角对等边
例:已知底边及底边上的高,用尺规作等腰三角形.如图所示,已知线段a和h.
求作等腰三角形ABC,使BC=a,高AD=h.
解:作法:
(1)作线段BC=a.
(2)作线段BC的垂直平分线MD,
垂足为点D.
(3)在DM上截取DA=h.
(4)连接AC,BC.
则△ABC就是所求作的等腰三角形.如图(2)所示.
图(2)
课堂小结
1.等腰三角形的判定定理:如果一个三角形有两个角相等,那么这个三角形是等腰三角形.其中,两个相等的角所对的边相等.(简称“等角对等边”)
说明:
(1)等腰三角形的判定定理与性质定理互逆;
(2)在判定定理的应用中,可以作底边上的高,也可以作顶角平分线,但不能作底边上的中线;
(3)判定定理在同一个三角形中才能适用.
2.等边三角形的判定定理
(1)三个角都相等的三角形是等边三角形.
(2)有一个角等于60°的等腰三角形是等边三角形.
检测反馈
1.如图所示,在△ABC中,AB=AC,点D,E在BC边
上, ∠ABD=∠DAE=∠EAC=36°,则图中等腰
三角形的个数是 ( )
A.4个 B.5个
C.6个 D.7个
C
解析:∵AB=AC,∠ABC=36°,∴∠ACB=36°,
∠BAC=108°,∵∠DAE=∠EAC=36°,
∴∠BAD=∠DAE=∠EAC=36°∴∠ADE=∠AED=72°,
∴△ABC, △ABD, △ADE, △ACE, △ACD, △ABE均是等腰三角形,共有6个.故选C.
2.如图所示,一艘海轮位于灯塔P的南偏东70°方向的M处,它以每小时40海里的速度向正北方向航行,2小时后到达位于灯塔P的北偏东40°的N处,则N与灯塔P的距离为( )
A.40海里 B.60海里
C.70海里 D.80海里
D
解析:MN=2×40=80(海里),由题意知∠M=70°,∠N=40°,
∴∠NPM=180°-∠M-∠N=180°- 70°- 40°=70°,
∴∠NPM=∠M,∴NP=MN=80海里.故选D.
3.如图所示,E是等边三角形ABC中AC边上的点,∠1=∠2,BE=CD,则△ADE的形状是( )
A.等腰三角形 B.等边三角形
C.不等腰三角形 D.不能确定形状
B
解析:∵△ABC为等边三角形,∴AB=AC.
∵∠1=∠2,BE=CD,∴△ABE≌△ACD,∴AE=AD,
∠BAE=∠CAD=60°,∴△ADE是等边三角形.故选B.
4.已知△ABC中,AB=AC,下列结论:
(1)若AB=BC,则△ABC是等边三角形;
(2)若∠A=60°,则△ABC是等边三角形;
(3)若∠B=60°,则△ABC是等边三角形.
其中正确的有 ( )
A.0个 B.1个 C.2个 D.3个
解析:因为AB=AC,AB=BC,所以AB=AC=BC,
所以△ABC是等边三角形,所以(1)正确;
因为AB=AC, ∠A=60°,所以△ABC是等边三角形,所以(2)正确;因为AB=AC∠B=60°,
所以△ABC是等边三角形,所以(3)正确.
正确的有3个.
D
谢 谢
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
