14.3因式分解--平方差公式法
文档属性
| 名称 | 14.3因式分解--平方差公式法 |  | |
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-11-28 09:40:11 | ||
图片预览








文档简介
课件25张PPT。14.3.2 公式法酉溪中学 粟深国2、判断下列变形过程,哪些是因式分解?
(1) (x+2)(x-2)=x2- 4 ( )
(2) x2- 4+3x=(x+2)(x-2)+3x ( )
(3) 7m-7n-7=7(m-n-1) ( )
(4) 4x2- 9 =(2x+3)(2x- 3 ) ( )××√√1:什么叫多项式的因式分解?把一个多项式化为几个整式乘积的形式,叫做多项式的因式分解复习回顾:你们能快速计算:
752- 252 =?吗?情景设置752- 252 =(75+25)(75-25)a2- b2=(a + b)( a - b)观察这个等式,从左到右是分解因式吗?
这和我们以前学过的什么知识很相似?利用平方差公式的逆运算—→分解因式总结:数字变字母:用平方差公式
进行因式分解学习目标:1、探索能用平方差公式进行因式分解的多项式特征。
2、正确熟练运用平方差公式进行分解因式。平方差公式:
(a+b)(a-b) = a2 - b2两个数的和与这两个数的差的积,等于这两个数的平方差。公式结构特点:等式左边是:两个数的和与这两个 数的差的积
等式右边是:这两个数的平方差做一做:根据平方差公式做下列练习 (a+3)(a-3)=
(2x+y)(2x-y)=a2 -9 (2x)2-y2=4x2-y2 试一试:
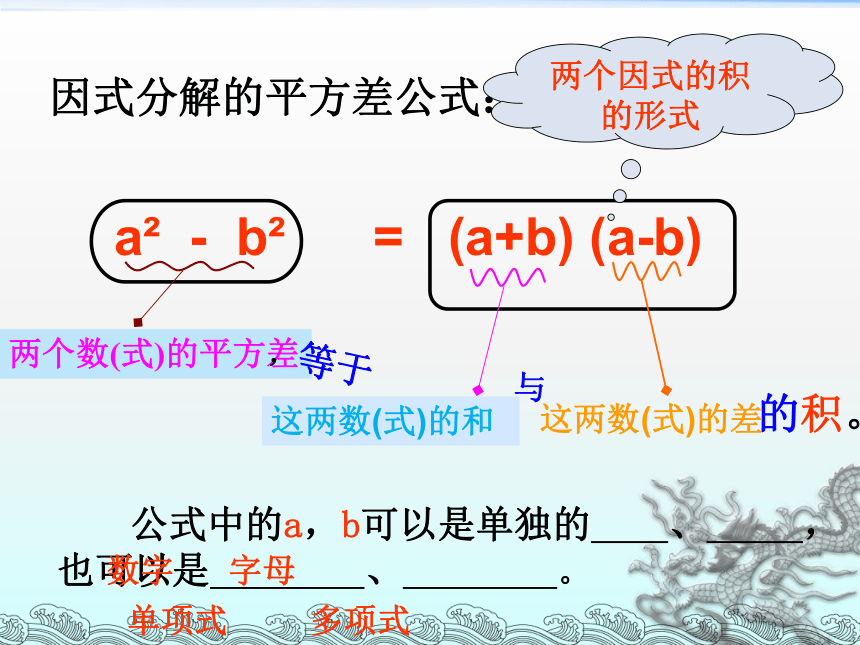
根据上面结果,你会做下面因式分解吗?a2 -9= ( )( )4x2-y2= ( )( )a+3a-32x+y 2x-ya2- b2 =(a +b) (a - b)因式分解的平方差公式:a2 - b2 = (a+b) (a-b)两个因式的积的形式这两数(式)的和这两数(式)的差 公式中的a,b可以是单独的 、 ,也可以是 、 。数字字母单项式多项式两个数(式)的平方差,等于与的积。不可以可 以不可以可 以可 以探索练习:。答:1. 多项式只有两项,两项符号相反
2.两部分都可写某个式子(或数)的平方运用a2-b2=(a+b)(a-b)公式时,如何区分a、b?答: a平方前符号为正,b平方前符号为负。
因式分解的平方差公式:a2 - b2 = (a+b) (a-b)具备什么特征的多项式是平方差式?
=( )2-( )2
=( )2-( )2
x2y20.1y练习:
2x5m a0.7b(1) 1-25x2解: 1-25x2
1、把两项写成平方的形式,找出a和b 2、利用a2-b2=(a-b)(a+b)
分解因式 =12-(5x)2=(1+5x)(1-5x)(2)4x2- m2n2=(2x)2-(mn)2
=(2x+mn)(2x-mn)法一:原式=+1-25x2(前后两项利用加法交换律交换位置) =12-(5x)2
=(1+5x)(1-5x)法二:原式=-( 25x2 )(把各项先提出一个“负号”)=-[(5x)2-12]=-(5x+1)(5x-1)-1例3:分解因式: (1) x5-x3解:(1)x5-x3 =x3(x2 –1)= x3 (x+1)(x-1)结论:1、若有公因式,要先提公因式,再考虑平方差公式.2、分解因式分解到不能分解为止.2x4-32y4
例题讲解=2(x2+4y2)(x2-4y2)= 2(x2+4y2)(x+2y)(x-2y)=2(x4-16y4) 判断下列各式是否可以
运用平方差公式进行因式分解① x2 + 4
② – 4x2 + y2
③ x4 – 1
④ x2 – x6
⑤ 6x3 – 54xy2
⑥ (x+p)2 – (x–q)2= y2 – 4x2 = (y+2x)(y–2x)
= (x2)2 – 12 = (x2+1) (x2–1)② – 4x2 + y2
③ x4 – 1(x2–1)= – ( 4x2 – y2 ) = – (2x+y)(2x–y)(x+1)(x–1)因式分解一定要分解彻底 !④ x2 – x6
= x2 – (x3)2
= (x+x3)(x–x3)
= x·(1+x2)·x·(1–x2)
= x2(1+x2)(1+x)(1–x)④ x2 – x6
= x2 (1–x4)
= x2 (1+x2)(1–x2)
= x2 (1+x2)(1+x)(1–x)更简便! 在我们现学过的因式分解方法中,先考虑提取公因式,再考虑用公式法。⑤ 6x3 – 54xy2
= 6x (x2–9y2)
= 6x (x+3y)(x–3y)
⑥ (x+p)2 – (x–q)2
= [ (x+p)+(x–q) ]·[ (x+p)–(x–q) ]
= (2x+p–q)(p+q)YXYXYX做一做 利用平方差公式因式分解。1.把下列各式分解因式
(1)16a2- 1 (4) a3x2 – a3y2
( 2 ) 4x2- m2n2
( 3 ) –9x2 + 4
解:(1)16a2-1=(4a)2 - 1
=(4a+1)(4a-1)解:(2) 4x2- m2n2
=(2x)2 - (mn)2
=(2x+mn)(2x-mn)解:(3) –9x2 + 4
(加法交换律)
= 22 – ( 3x ) 2
=(2+3x)(2-3x)=4 - 9x2 牛刀小试解:a3x2 – a3y2=a3 (x2 –y2)=a3 (x+y)(x-y)有公因式的要先提公因式把下列多项式因式分解:
1、9m2 –n2
2、 – a4 + 16
3、 a4x2 - a4y2
4、 (a+b) 2 – (a-b) 2
当堂训练:证明:两个连续奇数的平方差是8的倍数探究本节课我都
学到了什么?
1.能用平方差公式分解因式的多项式特点。
2.若多项式中有公因式,应先考虑提取公因式,
然后再进一步分解因式。
3.分解因式要彻底,直到不能再分解为止。:小结:
(1) (x+2)(x-2)=x2- 4 ( )
(2) x2- 4+3x=(x+2)(x-2)+3x ( )
(3) 7m-7n-7=7(m-n-1) ( )
(4) 4x2- 9 =(2x+3)(2x- 3 ) ( )××√√1:什么叫多项式的因式分解?把一个多项式化为几个整式乘积的形式,叫做多项式的因式分解复习回顾:你们能快速计算:
752- 252 =?吗?情景设置752- 252 =(75+25)(75-25)a2- b2=(a + b)( a - b)观察这个等式,从左到右是分解因式吗?
这和我们以前学过的什么知识很相似?利用平方差公式的逆运算—→分解因式总结:数字变字母:用平方差公式
进行因式分解学习目标:1、探索能用平方差公式进行因式分解的多项式特征。
2、正确熟练运用平方差公式进行分解因式。平方差公式:
(a+b)(a-b) = a2 - b2两个数的和与这两个数的差的积,等于这两个数的平方差。公式结构特点:等式左边是:两个数的和与这两个 数的差的积
等式右边是:这两个数的平方差做一做:根据平方差公式做下列练习 (a+3)(a-3)=
(2x+y)(2x-y)=a2 -9 (2x)2-y2=4x2-y2 试一试:
根据上面结果,你会做下面因式分解吗?a2 -9= ( )( )4x2-y2= ( )( )a+3a-32x+y 2x-ya2- b2 =(a +b) (a - b)因式分解的平方差公式:a2 - b2 = (a+b) (a-b)两个因式的积的形式这两数(式)的和这两数(式)的差 公式中的a,b可以是单独的 、 ,也可以是 、 。数字字母单项式多项式两个数(式)的平方差,等于与的积。不可以可 以不可以可 以可 以探索练习:。答:1. 多项式只有两项,两项符号相反
2.两部分都可写某个式子(或数)的平方运用a2-b2=(a+b)(a-b)公式时,如何区分a、b?答: a平方前符号为正,b平方前符号为负。
因式分解的平方差公式:a2 - b2 = (a+b) (a-b)具备什么特征的多项式是平方差式?
=( )2-( )2
=( )2-( )2
x2y20.1y练习:
2x5m a0.7b(1) 1-25x2解: 1-25x2
1、把两项写成平方的形式,找出a和b 2、利用a2-b2=(a-b)(a+b)
分解因式 =12-(5x)2=(1+5x)(1-5x)(2)4x2- m2n2=(2x)2-(mn)2
=(2x+mn)(2x-mn)法一:原式=+1-25x2(前后两项利用加法交换律交换位置) =12-(5x)2
=(1+5x)(1-5x)法二:原式=-( 25x2 )(把各项先提出一个“负号”)=-[(5x)2-12]=-(5x+1)(5x-1)-1例3:分解因式: (1) x5-x3解:(1)x5-x3 =x3(x2 –1)= x3 (x+1)(x-1)结论:1、若有公因式,要先提公因式,再考虑平方差公式.2、分解因式分解到不能分解为止.2x4-32y4
例题讲解=2(x2+4y2)(x2-4y2)= 2(x2+4y2)(x+2y)(x-2y)=2(x4-16y4) 判断下列各式是否可以
运用平方差公式进行因式分解① x2 + 4
② – 4x2 + y2
③ x4 – 1
④ x2 – x6
⑤ 6x3 – 54xy2
⑥ (x+p)2 – (x–q)2= y2 – 4x2 = (y+2x)(y–2x)
= (x2)2 – 12 = (x2+1) (x2–1)② – 4x2 + y2
③ x4 – 1(x2–1)= – ( 4x2 – y2 ) = – (2x+y)(2x–y)(x+1)(x–1)因式分解一定要分解彻底 !④ x2 – x6
= x2 – (x3)2
= (x+x3)(x–x3)
= x·(1+x2)·x·(1–x2)
= x2(1+x2)(1+x)(1–x)④ x2 – x6
= x2 (1–x4)
= x2 (1+x2)(1–x2)
= x2 (1+x2)(1+x)(1–x)更简便! 在我们现学过的因式分解方法中,先考虑提取公因式,再考虑用公式法。⑤ 6x3 – 54xy2
= 6x (x2–9y2)
= 6x (x+3y)(x–3y)
⑥ (x+p)2 – (x–q)2
= [ (x+p)+(x–q) ]·[ (x+p)–(x–q) ]
= (2x+p–q)(p+q)YXYXYX做一做 利用平方差公式因式分解。1.把下列各式分解因式
(1)16a2- 1 (4) a3x2 – a3y2
( 2 ) 4x2- m2n2
( 3 ) –9x2 + 4
解:(1)16a2-1=(4a)2 - 1
=(4a+1)(4a-1)解:(2) 4x2- m2n2
=(2x)2 - (mn)2
=(2x+mn)(2x-mn)解:(3) –9x2 + 4
(加法交换律)
= 22 – ( 3x ) 2
=(2+3x)(2-3x)=4 - 9x2 牛刀小试解:a3x2 – a3y2=a3 (x2 –y2)=a3 (x+y)(x-y)有公因式的要先提公因式把下列多项式因式分解:
1、9m2 –n2
2、 – a4 + 16
3、 a4x2 - a4y2
4、 (a+b) 2 – (a-b) 2
当堂训练:证明:两个连续奇数的平方差是8的倍数探究本节课我都
学到了什么?
1.能用平方差公式分解因式的多项式特点。
2.若多项式中有公因式,应先考虑提取公因式,
然后再进一步分解因式。
3.分解因式要彻底,直到不能再分解为止。:小结:
