24.2.2直线和圆的位置关系--切线的判定
文档属性
| 名称 | 24.2.2直线和圆的位置关系--切线的判定 |

|
|
| 格式 | zip | ||
| 文件大小 | 450.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-11-27 00:00:00 | ||
图片预览



文档简介
课件16张PPT。24.2.2
直线与圆的位置关系
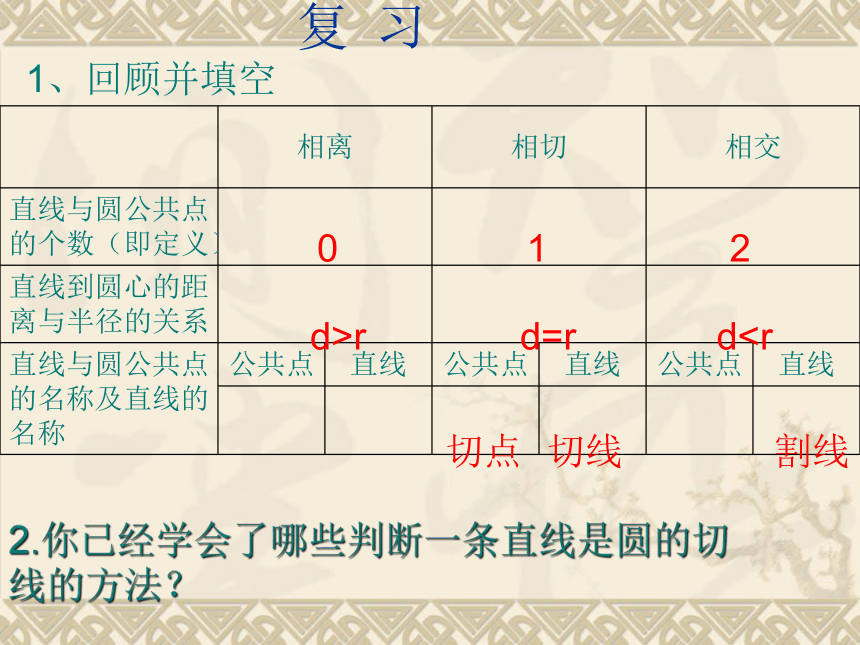
---切线的判定 复 习2.你已经学会了哪些判断一条直线是圆的切线的方法?1、回顾并填空012d>rd2 、当你在下雨天快速转动雨伞时水飞出的方向是什么方向?
请在⊙O上任意取一点A,连接OA。过点A作直线 l⊥OA。思考下列问题:
1. 圆心O到直线l的距离和圆的半径有什么数量关系?
2.直线l和圆O有什么位置关系?为什么?
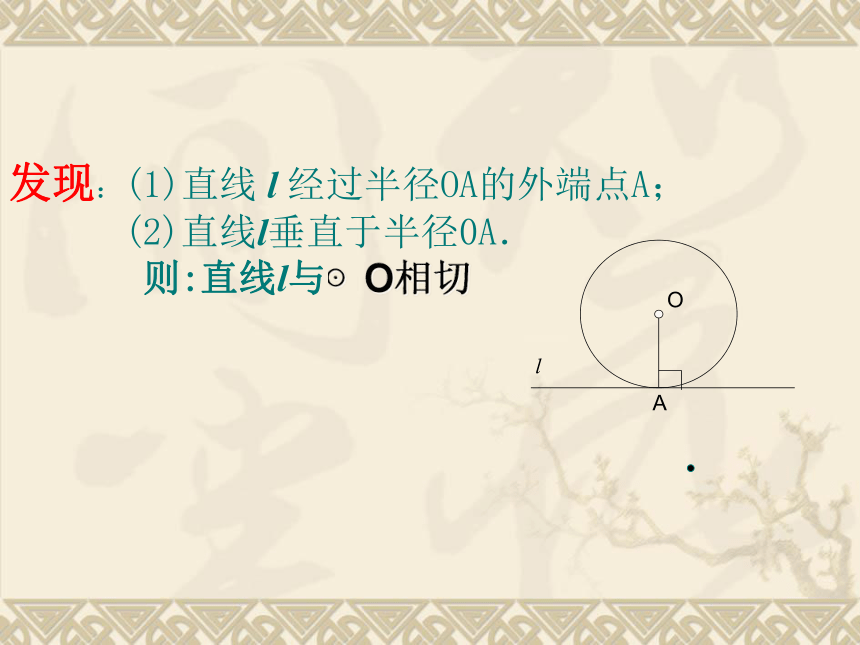
3. 由此你发现了什么?l发现:(1)直线 l 经过半径OA的外端点A;
(2)直线l垂直于半径0A.
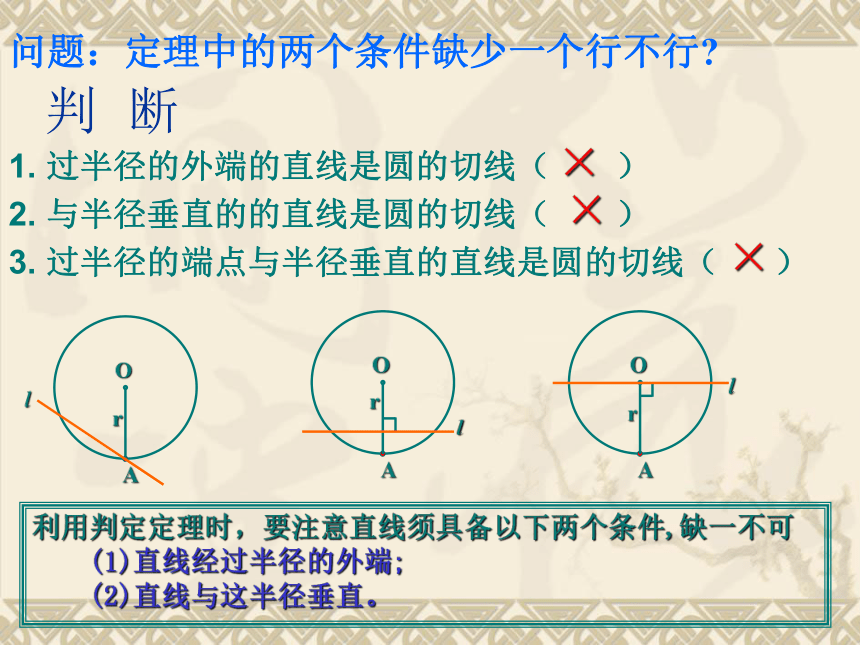
则:直线l与⊙O相切判 断1. 过半径的外端的直线是圆的切线( )
2. 与半径垂直的的直线是圆的切线( )
3. 过半径的端点与半径垂直的直线是圆的切线( )×××利用判定定理时,要注意直线须具备以下两个条件,缺一不可
(1)直线经过半径的外端;
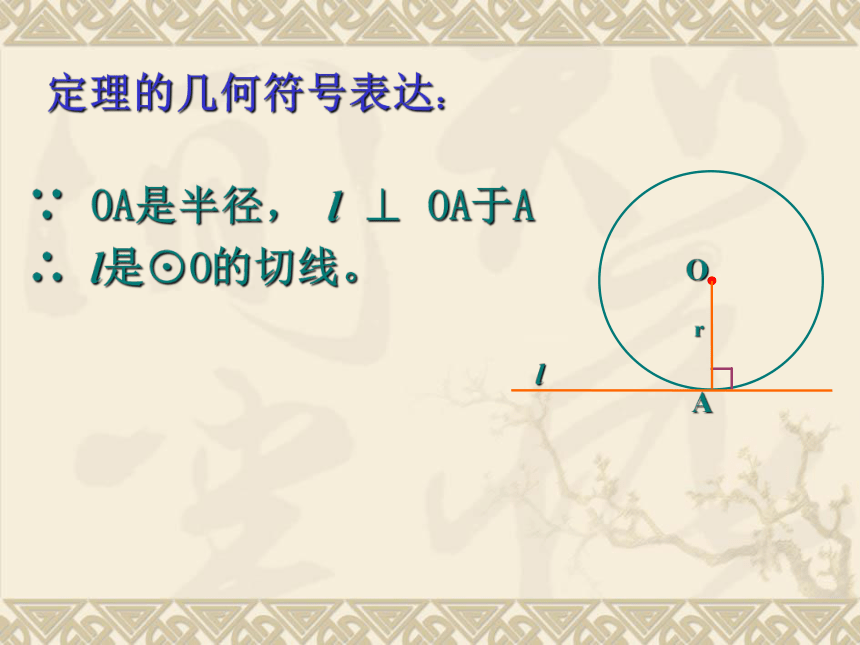
(2)直线与这半径垂直。问题:定理中的两个条件缺少一个行不行? Orl A∵ OA是半径, l ⊥ OA于A
∴ l是⊙O的切线。定理的几何符号表达:
切线的判定方法有三种:
①直线与圆有唯一公共点;
②直线到圆心的距离等于该圆的半径;
③切线的判定定理.即
经过半径的外端并且垂直这条半径的直线是圆的切线
判定直线与圆相切有哪些方法? 如图,如果直线l是圆的切线,切点为A,那么半径OA与直线l是 不是一定垂直呢?逆向思维〖例1〗已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB。
求证:直线AB是⊙O的切线。OBAC分析:由于AB过⊙O上的点C,所以连接OC,只要证明
AB⊥OC即可。 证明:连结OC(如图)。
∵ ⊿OAB中, OA=OB , CA=CB,
∴ AB⊥OC。
∵ OC是⊙O的半径
∴ AB是⊙O的切线。〖例2〗已知:O为∠BAC平分线上一点,OD⊥AB于D,以O为圆心,OD为
半径作⊙O。
求证:⊙O与AC相切。OABCD证明:过O作OE⊥AC于E。
∵ AO平分∠BAC,OD⊥AB
∴ OE=OD
即圆心O到AC的距离 d = r
∴ AC是⊙O切线。小 结例1与例2的证法有何不同?
(1)如果已知直线经过圆上一点,则连结这点和圆心,得到辅助半径,再证所作半径与这直线垂直。简记为:连半径,证垂直。
(2)如果已知条件中不知直线与圆是否有公共点,则过圆心作直线的垂线段为辅助线,再证垂线段长等于半径长。简记为:作垂直,证半径。学以致用:小红家的锅盖坏了,为了配一个锅盖,
需要测量锅盖(锅边所形成的圆) 的直径,而小红家只
有一把长20cm 的直尺,根本不够长,怎么办呢?
小红想了想,采取以下方法:
首先把锅平放到墙根,锅边刚好靠到两墙,用直尺紧贴墙面
量得MA的长,即可求出锅盖的直径,请你利用下图,说明她
这样做的道理. O课堂小结1、定义法:和圆有且只有一个公共点的直线是圆的切线。
2、数量法(d=r):和圆心距离等于半径的直线是圆的切线。
3、判定定理:经过半径外端且垂直于这条半径的直线是圆的切线。一、证明直线与圆相切方法1、切线和圆只有一个公共点。2、切线和圆心的距离等于半径。3、切线垂直于过切点的半径。二、切线的性质: 1 当你在下雨天快速转动雨伞时水飞出的方向是什么方向?
2 砂轮打磨工件飞出火星的方向是什么方向?现在你知道: 下雨天转动雨伞时飞出的水,以及在砂轮上打磨工件飞 出的火星,均沿着圆的切线的方向飞出.Class over
88!
请在⊙O上任意取一点A,连接OA。过点A作直线 l⊥OA。思考下列问题:
1. 圆心O到直线l的距离和圆的半径有什么数量关系?
2.直线l和圆O有什么位置关系?为什么?
3. 由此你发现了什么?l发现:(1)直线 l 经过半径OA的外端点A;
(2)直线l垂直于半径0A.
则:直线l与⊙O相切判 断1. 过半径的外端的直线是圆的切线( )
2. 与半径垂直的的直线是圆的切线( )
3. 过半径的端点与半径垂直的直线是圆的切线( )×××利用判定定理时,要注意直线须具备以下两个条件,缺一不可
(1)直线经过半径的外端;
(2)直线与这半径垂直。问题:定理中的两个条件缺少一个行不行? Orl A∵ OA是半径, l ⊥ OA于A
∴ l是⊙O的切线。定理的几何符号表达:
切线的判定方法有三种:
①直线与圆有唯一公共点;
②直线到圆心的距离等于该圆的半径;
③切线的判定定理.即
经过半径的外端并且垂直这条半径的直线是圆的切线
判定直线与圆相切有哪些方法? 如图,如果直线l是圆的切线,切点为A,那么半径OA与直线l是 不是一定垂直呢?逆向思维〖例1〗已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB。
求证:直线AB是⊙O的切线。OBAC分析:由于AB过⊙O上的点C,所以连接OC,只要证明
AB⊥OC即可。 证明:连结OC(如图)。
∵ ⊿OAB中, OA=OB , CA=CB,
∴ AB⊥OC。
∵ OC是⊙O的半径
∴ AB是⊙O的切线。〖例2〗已知:O为∠BAC平分线上一点,OD⊥AB于D,以O为圆心,OD为
半径作⊙O。
求证:⊙O与AC相切。OABCD证明:过O作OE⊥AC于E。
∵ AO平分∠BAC,OD⊥AB
∴ OE=OD
即圆心O到AC的距离 d = r
∴ AC是⊙O切线。小 结例1与例2的证法有何不同?
(1)如果已知直线经过圆上一点,则连结这点和圆心,得到辅助半径,再证所作半径与这直线垂直。简记为:连半径,证垂直。
(2)如果已知条件中不知直线与圆是否有公共点,则过圆心作直线的垂线段为辅助线,再证垂线段长等于半径长。简记为:作垂直,证半径。学以致用:小红家的锅盖坏了,为了配一个锅盖,
需要测量锅盖(锅边所形成的圆) 的直径,而小红家只
有一把长20cm 的直尺,根本不够长,怎么办呢?
小红想了想,采取以下方法:
首先把锅平放到墙根,锅边刚好靠到两墙,用直尺紧贴墙面
量得MA的长,即可求出锅盖的直径,请你利用下图,说明她
这样做的道理. O课堂小结1、定义法:和圆有且只有一个公共点的直线是圆的切线。
2、数量法(d=r):和圆心距离等于半径的直线是圆的切线。
3、判定定理:经过半径外端且垂直于这条半径的直线是圆的切线。一、证明直线与圆相切方法1、切线和圆只有一个公共点。2、切线和圆心的距离等于半径。3、切线垂直于过切点的半径。二、切线的性质: 1 当你在下雨天快速转动雨伞时水飞出的方向是什么方向?
2 砂轮打磨工件飞出火星的方向是什么方向?现在你知道: 下雨天转动雨伞时飞出的水,以及在砂轮上打磨工件飞 出的火星,均沿着圆的切线的方向飞出.Class over
88!
同课章节目录
