23.1图形的旋转(2节课)[上学期]
文档属性
| 名称 | 23.1图形的旋转(2节课)[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 524.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-09-13 00:00:00 | ||
图片预览






文档简介
(共23张PPT)
自转与公转
(1)上面情景中的转动现象,有什么共同的特征?
(2)钟表的指针、秋千在转动过程中,其形状、大小、位置是否发生变化呢?
(1)上面情景中的转动现象,有什么共同的特征?
(2)钟表的指针、秋千在
转动过程中,其形状、大小、
位置是否发生变化呢?
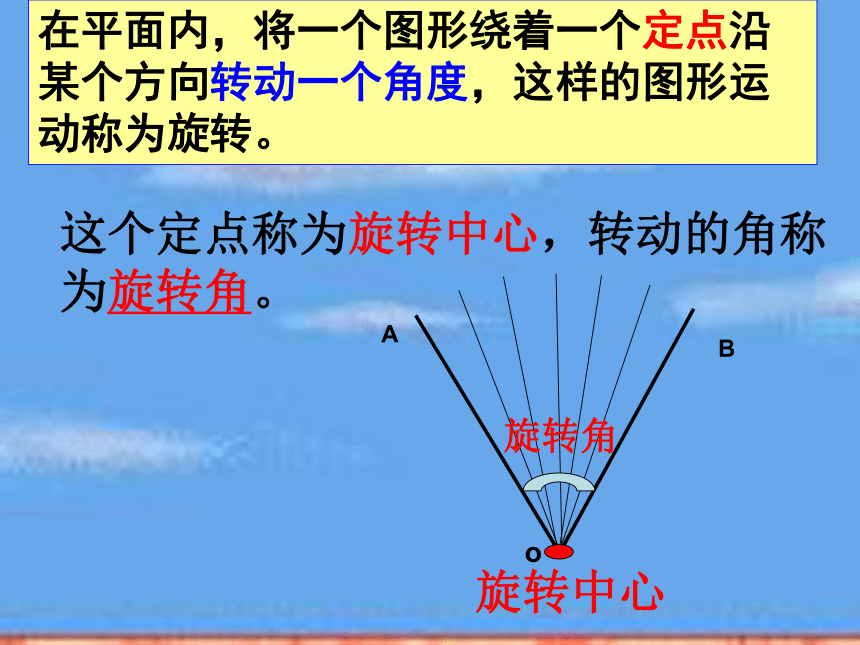
这个定点称为旋转中心,转动的角称为旋转角。
旋转角
旋转中心
在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动称为旋转。
A
o
B
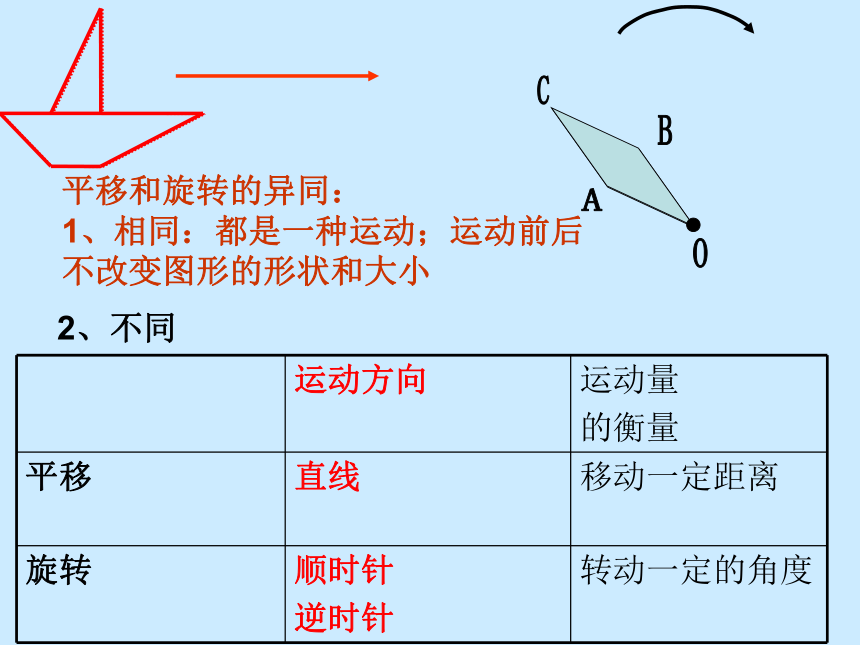
平移和旋转的异同:
1、相同:都是一种运动;运动前后 不改变图形的形状和大小
2、不同
运动方向 运动量
的衡量
平移 直线 移动一定距离
旋转 顺时针
逆时针 转动一定的角度
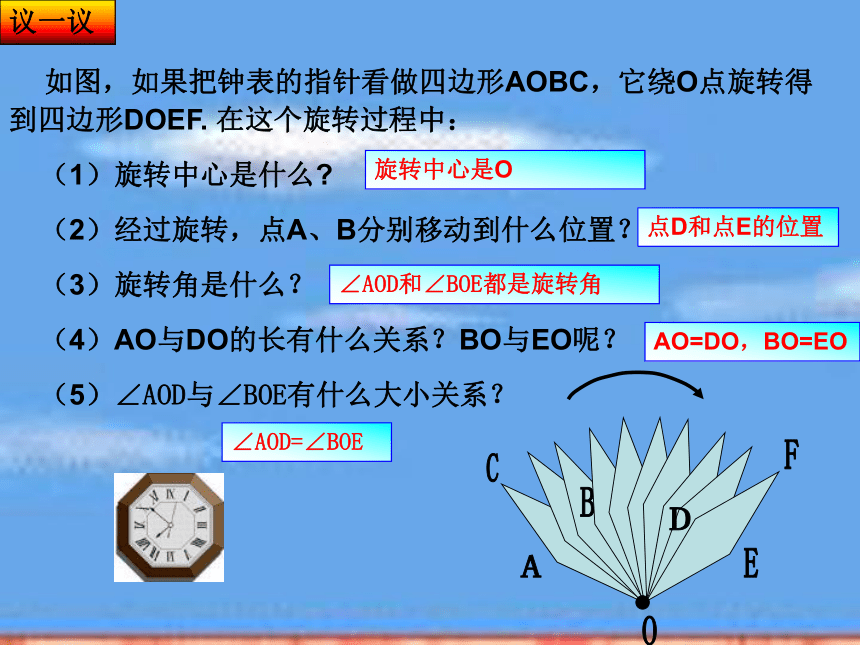
如图,如果把钟表的指针看做四边形AOBC,它绕O点旋转得 到四边形DOEF. 在这个旋转过程中:
(1)旋转中心是什么
(2)经过旋转,点A、B分别移动到什么位置?
(3)旋转角是什么?
(4)AO与DO的长有什么关系?BO与EO呢?
(5)∠AOD与∠BOE有什么大小关系?
议一议
旋转中心是O
点D和点E的位置
AO=DO,BO=EO
∠AOD=∠BOE
∠AOD和∠BOE都是旋转角
(4)对应点到旋转中心的距离相等.
旋转的基本性质
(1)旋转不改变图形的大小和形状.
(2)图形上的每一点都绕旋转中心沿相同方向转动了相同的角度
(3)任意一对对应点与旋转中心的连线所成的角度都是旋转角.
例1:钟表的分针匀速旋转一周需要60分.
(1)指出它的旋转中心;
(2)经过20分,分针旋转了多少度?
(2)分针匀速旋转一周需要60
分,因此旋转20分,分针
旋转的角度为
解:
(1)它的旋转中心是钟表的轴心;
可以看作是一个花瓣连续4次旋转所形成的,每次旋转分别等于720 , 1440 , 2160 , 2880
思考题:香港区徽可以看作是什么“基本图案”通过怎样的旋转而得到的?
P69 随堂练习:本图案可以看做是一个菱形通过几次旋转得到的?每次旋转了多少度?
也可以看做是二个相邻菱形通过几次旋转得到的?每次旋转了多少度?
还可以看做是几个菱形通过几次旋转得到的?每次旋转了多少度?
3个 1次 1800
2次 1200 , 2400
5次 600, 1200, 1800, 2400, 3000
3个 1次 600
P68 做一做:
在图中,正方形ABCD与正方形EFGH边长相等,这个图案可以看作是哪个“基本图案”通过旋转得到的.
试一试
图中是否存在这样的两个三角形,其中一个是通过另一个旋转得到的?
简单的旋转作图
项目 已知 未知 备注
源图形 ● 点A
源位置 ● 点A
旋转中心 ● 点O
旋转方向 ● 顺时针
旋转角度 ● 60
目标图形 ● 点
目标位置 ● 点B (求作)
A
O
点的旋转作法
例1 将A点绕O点沿顺时针方向旋转60 .
分析:
作法:
1. 以点O为圆心,OA长为半径画圆;
2. 连接OA, 用量角器或三角板(限
特殊角)作出∠AOB,与圆周交
于B点;
3. B点即为所求作.
B
简单的旋转作图
项目 已知 未知 备注
源图形 ● 线段AB
源位置 ● 线段AB
旋转中心 ● 点O
旋转方向 ● 顺时针
旋转角度 ● 60
目标图形 ● 线段
目标位置 ● 线段CD (求作)
A
O
线段的旋转作法
例2 将线段AB绕O点沿顺时针方向旋转60 .
分析:
作法:
将点A绕点O顺时针旋转60 ,得
点C;
2. 将点B绕点O顺时针旋转60 ,得点D ;
3. 连接CD, 则线段CD即为所求作.
C
B
D
简单的旋转作图
项目 已知 未知 备注
源图形 ● △ABC
源位置 ● △ABC
旋转中心 ● 点C
旋转方向 ● 根据A与D的对应关系判断为顺时针
旋转角度 ● ∠ACD
目标图形 ● 三角形
目标位置 ● △DEC (求作)
图形的旋转作法
例3 如图,△ABC绕C点旋转后,顶点A得对应点为点D. 试确定顶点B对应点的位置以及旋转后的三角形.
分析:
作法一:
1. 连接CD;
2. 以CB为一边,作∠BCE,使得∠BCE=∠ACD ;
3. 在射线CB上截取CE,使得CE=CB;
4. 连接DE,则△DEC即为所求作.
C
A
B
D
E
简单的旋转作图
练习1
将下图中大写字母N绕它右下侧的顶点按顺时针方向旋转90 ,作出旋转后的图案.
课堂回顾:这节课,主要学习了什么?
在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动称为旋转
旋转的概念:
旋转的性质:
1、旋转不改变图形的大小和形状.
2、任意一对对应点与旋转中心的连线所成的
角度都是旋转角,旋转角相等.
3、对应点到旋转中心的距离相等
自转与公转
(1)上面情景中的转动现象,有什么共同的特征?
(2)钟表的指针、秋千在转动过程中,其形状、大小、位置是否发生变化呢?
(1)上面情景中的转动现象,有什么共同的特征?
(2)钟表的指针、秋千在
转动过程中,其形状、大小、
位置是否发生变化呢?
这个定点称为旋转中心,转动的角称为旋转角。
旋转角
旋转中心
在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动称为旋转。
A
o
B
平移和旋转的异同:
1、相同:都是一种运动;运动前后 不改变图形的形状和大小
2、不同
运动方向 运动量
的衡量
平移 直线 移动一定距离
旋转 顺时针
逆时针 转动一定的角度
如图,如果把钟表的指针看做四边形AOBC,它绕O点旋转得 到四边形DOEF. 在这个旋转过程中:
(1)旋转中心是什么
(2)经过旋转,点A、B分别移动到什么位置?
(3)旋转角是什么?
(4)AO与DO的长有什么关系?BO与EO呢?
(5)∠AOD与∠BOE有什么大小关系?
议一议
旋转中心是O
点D和点E的位置
AO=DO,BO=EO
∠AOD=∠BOE
∠AOD和∠BOE都是旋转角
(4)对应点到旋转中心的距离相等.
旋转的基本性质
(1)旋转不改变图形的大小和形状.
(2)图形上的每一点都绕旋转中心沿相同方向转动了相同的角度
(3)任意一对对应点与旋转中心的连线所成的角度都是旋转角.
例1:钟表的分针匀速旋转一周需要60分.
(1)指出它的旋转中心;
(2)经过20分,分针旋转了多少度?
(2)分针匀速旋转一周需要60
分,因此旋转20分,分针
旋转的角度为
解:
(1)它的旋转中心是钟表的轴心;
可以看作是一个花瓣连续4次旋转所形成的,每次旋转分别等于720 , 1440 , 2160 , 2880
思考题:香港区徽可以看作是什么“基本图案”通过怎样的旋转而得到的?
P69 随堂练习:本图案可以看做是一个菱形通过几次旋转得到的?每次旋转了多少度?
也可以看做是二个相邻菱形通过几次旋转得到的?每次旋转了多少度?
还可以看做是几个菱形通过几次旋转得到的?每次旋转了多少度?
3个 1次 1800
2次 1200 , 2400
5次 600, 1200, 1800, 2400, 3000
3个 1次 600
P68 做一做:
在图中,正方形ABCD与正方形EFGH边长相等,这个图案可以看作是哪个“基本图案”通过旋转得到的.
试一试
图中是否存在这样的两个三角形,其中一个是通过另一个旋转得到的?
简单的旋转作图
项目 已知 未知 备注
源图形 ● 点A
源位置 ● 点A
旋转中心 ● 点O
旋转方向 ● 顺时针
旋转角度 ● 60
目标图形 ● 点
目标位置 ● 点B (求作)
A
O
点的旋转作法
例1 将A点绕O点沿顺时针方向旋转60 .
分析:
作法:
1. 以点O为圆心,OA长为半径画圆;
2. 连接OA, 用量角器或三角板(限
特殊角)作出∠AOB,与圆周交
于B点;
3. B点即为所求作.
B
简单的旋转作图
项目 已知 未知 备注
源图形 ● 线段AB
源位置 ● 线段AB
旋转中心 ● 点O
旋转方向 ● 顺时针
旋转角度 ● 60
目标图形 ● 线段
目标位置 ● 线段CD (求作)
A
O
线段的旋转作法
例2 将线段AB绕O点沿顺时针方向旋转60 .
分析:
作法:
将点A绕点O顺时针旋转60 ,得
点C;
2. 将点B绕点O顺时针旋转60 ,得点D ;
3. 连接CD, 则线段CD即为所求作.
C
B
D
简单的旋转作图
项目 已知 未知 备注
源图形 ● △ABC
源位置 ● △ABC
旋转中心 ● 点C
旋转方向 ● 根据A与D的对应关系判断为顺时针
旋转角度 ● ∠ACD
目标图形 ● 三角形
目标位置 ● △DEC (求作)
图形的旋转作法
例3 如图,△ABC绕C点旋转后,顶点A得对应点为点D. 试确定顶点B对应点的位置以及旋转后的三角形.
分析:
作法一:
1. 连接CD;
2. 以CB为一边,作∠BCE,使得∠BCE=∠ACD ;
3. 在射线CB上截取CE,使得CE=CB;
4. 连接DE,则△DEC即为所求作.
C
A
B
D
E
简单的旋转作图
练习1
将下图中大写字母N绕它右下侧的顶点按顺时针方向旋转90 ,作出旋转后的图案.
课堂回顾:这节课,主要学习了什么?
在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动称为旋转
旋转的概念:
旋转的性质:
1、旋转不改变图形的大小和形状.
2、任意一对对应点与旋转中心的连线所成的
角度都是旋转角,旋转角相等.
3、对应点到旋转中心的距离相等
同课章节目录
