苏教版(2019)必修第一册4.2 对数 课件(共27张PPT)
文档属性
| 名称 | 苏教版(2019)必修第一册4.2 对数 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-06 08:04:49 | ||
图片预览








文档简介
(共27张PPT)
第4章
4.2
对 数
学习目标
1.理解对数的概念,能够熟练地转化指数式与对数式.
2.理解对数的运算性质.
3.知道用换底公式能将一般对数转化成自然对数或常用对数.
4.了解对数在简化运算中的作用.
核心素养:数学抽象、数学运算
新知学习
一、对数的概念
1.对数的概念
一般地,如果ab=N(a>0,a≠1),那么就称b
是以a为底N的对数,记作logaN=b,其中,a叫作对数的底数,N叫作真数.
【说明】规定a>0且a≠1是因为:
(1)若a<0,则当N为某些值时,b的值不存在.如:b=log(-2)8不存在.
(2)若a=0,则①当N≠0时,b的值不存在.如:log03(可理解为0的多少次幂是3)不存在.
②当N=0时,b可以是除零以外的任意实数,是不唯一的,即log00有无数个值.
(3)若a=1,则①当N≠1时,b的值不存在.如:log13不存在.
②当N=1时,b可以为任意实数,是不唯一的,即log11有无数个值.
因此规定a>0,且a≠1.
示例 在b=loga-2(5-a)中,实数a的取值范围是 .
(2,3)∪(3,5)
2.指数式与对数式的关系
根据对数的定义,可以得到对数与指数间的关系:当a>0,a≠1时,ab=N?b=logaN.
在ab=N与b=logaN中,a,b,N是同一个代表符号,只是有不同的名称.
【注意】并非所有的指数式都可以直接化为对数式,如(-3)2=9就不能直接写成log-39=2,只有符合a>0,a≠1,才有ab=N?b=logaN.
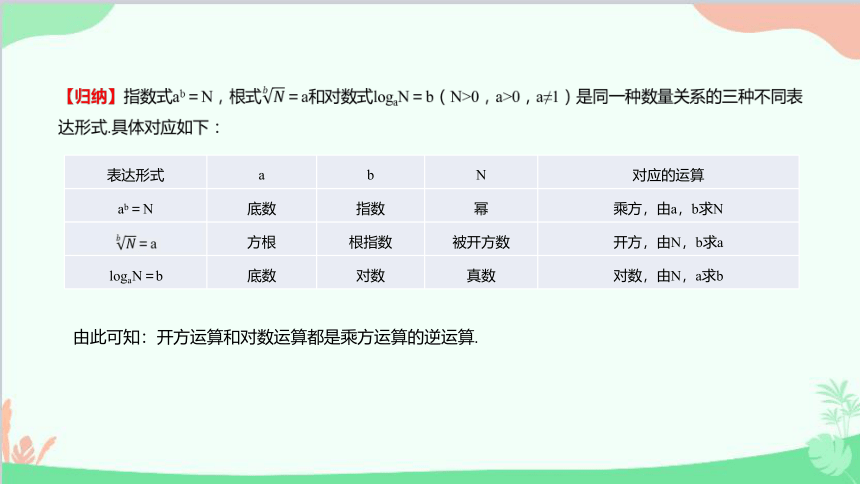
表达形式 a b N 对应的运算
ab=N 底数 指数 幂 乘方,由a,b求N
方根 根指数 被开方数 开方,由N,b求a
logaN=b 底数 对数 真数 对数,由N,a求b
由此可知:开方运算和对数运算都是乘方运算的逆运算.
3.自然对数与常用对数
名称 定义 符号
常用对数 以10为底的对数叫作常用对数 log10N记为lg N
自然对数 以e为底的对数叫作自然对数,e是无理数,e=2.718 28… logeN记为ln N
【方法技巧】求对数式logaN(a>0,且a≠1,N>0)的值的步骤
(1)设logaN=m;
(2)将logaN=m写成指数式am=N;
(3)将N写成以a为底的指数幂N=ab,则m=b,即logaN=b.
二、对数的运算性质
1.对数的运算性质
如果a>0且a≠1,M>0,N>0,α∈R,则
(1)loga(MN)=logaM+logaN. 即两个正因数积的对数等于同一底数的这两个正因数对数的和.
2.对数运算性质与指数运算性质的对比
表达式 ab=N logaN=b
运算法则 am·an=am+n loga(MN)=logaM+logaN
(am)n=amn logaM n=nlogaM
【巧记】 积的对数变加法,商的对数变减法;幂的乘方取对数,要把指数提到前.
A
【说明】换底公式的用途和本质
(1)换底公式的主要用途在于将一般对数式化为常用对数或自然对数,以此来解决对数求值问题.
(2)换底公式的本质在于改变对数式的底数,以便进行计算和证明.究竟以哪个数为底数,由已知条件来决定.一般换成以10为底的常用对数.
【知识拓展】(1)logab·logbc=logac(a>0且a≠1,b>0且b≠1,c>0).
(2)logab·logbc·logca=1(a>0且a≠1,b>0且b≠1,c>0且c≠1).
【注意】(1)利用换底公式可以把不同底的对数化为同底的对数,要注意换底公式的正用、逆用以及变形应用.
(2)题目中有指数式与对数式时,要注意将指数式与对数式进行互化,统一成一种形式.
典例剖析
【方法总结】(1)对于同底数的对数式,化简的常用方法:“收”,即逆用对数的运算性质将同底对数的和(差)“收”成积(商)的对数,即把多个对数式转化为一个对数式;“拆”,即正用对数的运算性质将对数式“拆”成较小真数的对数的和(差).(2)对常用对数的化简要创设情境,要充分利用“lg 5+lg 2=1”来解题.(3)对含有多重对数符号的对数式,应从内向外逐层化简.
二、对数换底公式及其应用
例 2 计算:(log2125+log425+log85)×(log52+log254+log1258).
【方法技巧】利用换底公式,先将不同底数的对数式转化为同底数的对数式,将一般对数转化为自然对数或常用对数 ,然后运用对数的运算性质运算.要注意换底公式的正用、逆用及变形应用.
【技巧点拨】与对数相关的带有附加条件的代数式求值问题,需要对已知条件和所求式子进行化简转化,原则是化为同底的对数,以便利用对数的运算性质.要整体把握对数式的结构特征,灵活运用指数式与对数式的互化.
【解】(1)由方程,得log2(x+1)=log4(x+4)+1,
∴ log4(x+1)2=log4[4(x+4)],∴ (x+1)2=4(x+4),解得x=5或x=-3.
经检验,知x=-3不符合题意,舍去;x=5为原方程的解.故原方程的解为x=5.
(2)方程两边取常用对数,得[(lg x)3-2lg x]lg x=lg 0.1,
整理,得(lg x)4-2(lg x)2+1=0,∴ [(lg x)2-1]2=0,∴ (lg x)2=1,
则lg x=±1,解得x=10或x=0.1.
经检验,知x=10与x=0.1均为原方程的解.故原方程的解为x=10或x=0.1.
【点评】解对数方程就是将其转化为同底数的对数式求解,或通过换元转化为一般的代数方程求解,注意在将对数方程化为一般代数方程的过程中,未知数的范围扩大或缩小都容易产生增根或漏掉原方程的根,故解对数方程必须把所求的解代入原方程进行检验.
【方法技巧】对数方程的类型与解法
名称 类型 解法
基本型 loga f(x)=b 将对数式转化为指数式f(x)=ab,解出x(注意检验f(x)>0)
logf(x)n=b 将对数式化为指数式[f(x)]b=n,解出x(注意检验f(x)>0且f(x)≠1)
同底数型 loga f(x)=logaφ(x) 转化为f(x)=φ(x)求解(注意检验f(x)>0,φ(x)>0)
需代换型 f(logax)=0 换元,令t=logax,转化为关于t的方程f(t)=0,解得t=p,
再解方程logax=p,得到x=ap(注意检验a>0且a≠1,x>0)
取对数型 af(x)=bφ(x) 取常用对数得f(x)·lg a=φ(x)·lg b
五、对数的实际应用
例 5 某公司为激励创新,计划逐年加大研发资金投入.若该公司2019年全年投入研发资金130万元,在此基础上,每年投入的研发资金比上一年增长12%,则该公司全年投入的研发资金开始超过200万元的年份是( )(参考数据:lg 1.12≈0.05,lg 1.3≈0.11,lg 2≈0.30)
A.2021年 B.2022年 C.2023年 D.2024年
C
B
随堂小测
BD
B
A
ACD
A
谢 谢!
第4章
4.2
对 数
学习目标
1.理解对数的概念,能够熟练地转化指数式与对数式.
2.理解对数的运算性质.
3.知道用换底公式能将一般对数转化成自然对数或常用对数.
4.了解对数在简化运算中的作用.
核心素养:数学抽象、数学运算
新知学习
一、对数的概念
1.对数的概念
一般地,如果ab=N(a>0,a≠1),那么就称b
是以a为底N的对数,记作logaN=b,其中,a叫作对数的底数,N叫作真数.
【说明】规定a>0且a≠1是因为:
(1)若a<0,则当N为某些值时,b的值不存在.如:b=log(-2)8不存在.
(2)若a=0,则①当N≠0时,b的值不存在.如:log03(可理解为0的多少次幂是3)不存在.
②当N=0时,b可以是除零以外的任意实数,是不唯一的,即log00有无数个值.
(3)若a=1,则①当N≠1时,b的值不存在.如:log13不存在.
②当N=1时,b可以为任意实数,是不唯一的,即log11有无数个值.
因此规定a>0,且a≠1.
示例 在b=loga-2(5-a)中,实数a的取值范围是 .
(2,3)∪(3,5)
2.指数式与对数式的关系
根据对数的定义,可以得到对数与指数间的关系:当a>0,a≠1时,ab=N?b=logaN.
在ab=N与b=logaN中,a,b,N是同一个代表符号,只是有不同的名称.
【注意】并非所有的指数式都可以直接化为对数式,如(-3)2=9就不能直接写成log-39=2,只有符合a>0,a≠1,才有ab=N?b=logaN.
表达形式 a b N 对应的运算
ab=N 底数 指数 幂 乘方,由a,b求N
方根 根指数 被开方数 开方,由N,b求a
logaN=b 底数 对数 真数 对数,由N,a求b
由此可知:开方运算和对数运算都是乘方运算的逆运算.
3.自然对数与常用对数
名称 定义 符号
常用对数 以10为底的对数叫作常用对数 log10N记为lg N
自然对数 以e为底的对数叫作自然对数,e是无理数,e=2.718 28… logeN记为ln N
【方法技巧】求对数式logaN(a>0,且a≠1,N>0)的值的步骤
(1)设logaN=m;
(2)将logaN=m写成指数式am=N;
(3)将N写成以a为底的指数幂N=ab,则m=b,即logaN=b.
二、对数的运算性质
1.对数的运算性质
如果a>0且a≠1,M>0,N>0,α∈R,则
(1)loga(MN)=logaM+logaN. 即两个正因数积的对数等于同一底数的这两个正因数对数的和.
2.对数运算性质与指数运算性质的对比
表达式 ab=N logaN=b
运算法则 am·an=am+n loga(MN)=logaM+logaN
(am)n=amn logaM n=nlogaM
【巧记】 积的对数变加法,商的对数变减法;幂的乘方取对数,要把指数提到前.
A
【说明】换底公式的用途和本质
(1)换底公式的主要用途在于将一般对数式化为常用对数或自然对数,以此来解决对数求值问题.
(2)换底公式的本质在于改变对数式的底数,以便进行计算和证明.究竟以哪个数为底数,由已知条件来决定.一般换成以10为底的常用对数.
【知识拓展】(1)logab·logbc=logac(a>0且a≠1,b>0且b≠1,c>0).
(2)logab·logbc·logca=1(a>0且a≠1,b>0且b≠1,c>0且c≠1).
【注意】(1)利用换底公式可以把不同底的对数化为同底的对数,要注意换底公式的正用、逆用以及变形应用.
(2)题目中有指数式与对数式时,要注意将指数式与对数式进行互化,统一成一种形式.
典例剖析
【方法总结】(1)对于同底数的对数式,化简的常用方法:“收”,即逆用对数的运算性质将同底对数的和(差)“收”成积(商)的对数,即把多个对数式转化为一个对数式;“拆”,即正用对数的运算性质将对数式“拆”成较小真数的对数的和(差).(2)对常用对数的化简要创设情境,要充分利用“lg 5+lg 2=1”来解题.(3)对含有多重对数符号的对数式,应从内向外逐层化简.
二、对数换底公式及其应用
例 2 计算:(log2125+log425+log85)×(log52+log254+log1258).
【方法技巧】利用换底公式,先将不同底数的对数式转化为同底数的对数式,将一般对数转化为自然对数或常用对数 ,然后运用对数的运算性质运算.要注意换底公式的正用、逆用及变形应用.
【技巧点拨】与对数相关的带有附加条件的代数式求值问题,需要对已知条件和所求式子进行化简转化,原则是化为同底的对数,以便利用对数的运算性质.要整体把握对数式的结构特征,灵活运用指数式与对数式的互化.
【解】(1)由方程,得log2(x+1)=log4(x+4)+1,
∴ log4(x+1)2=log4[4(x+4)],∴ (x+1)2=4(x+4),解得x=5或x=-3.
经检验,知x=-3不符合题意,舍去;x=5为原方程的解.故原方程的解为x=5.
(2)方程两边取常用对数,得[(lg x)3-2lg x]lg x=lg 0.1,
整理,得(lg x)4-2(lg x)2+1=0,∴ [(lg x)2-1]2=0,∴ (lg x)2=1,
则lg x=±1,解得x=10或x=0.1.
经检验,知x=10与x=0.1均为原方程的解.故原方程的解为x=10或x=0.1.
【点评】解对数方程就是将其转化为同底数的对数式求解,或通过换元转化为一般的代数方程求解,注意在将对数方程化为一般代数方程的过程中,未知数的范围扩大或缩小都容易产生增根或漏掉原方程的根,故解对数方程必须把所求的解代入原方程进行检验.
【方法技巧】对数方程的类型与解法
名称 类型 解法
基本型 loga f(x)=b 将对数式转化为指数式f(x)=ab,解出x(注意检验f(x)>0)
logf(x)n=b 将对数式化为指数式[f(x)]b=n,解出x(注意检验f(x)>0且f(x)≠1)
同底数型 loga f(x)=logaφ(x) 转化为f(x)=φ(x)求解(注意检验f(x)>0,φ(x)>0)
需代换型 f(logax)=0 换元,令t=logax,转化为关于t的方程f(t)=0,解得t=p,
再解方程logax=p,得到x=ap(注意检验a>0且a≠1,x>0)
取对数型 af(x)=bφ(x) 取常用对数得f(x)·lg a=φ(x)·lg b
五、对数的实际应用
例 5 某公司为激励创新,计划逐年加大研发资金投入.若该公司2019年全年投入研发资金130万元,在此基础上,每年投入的研发资金比上一年增长12%,则该公司全年投入的研发资金开始超过200万元的年份是( )(参考数据:lg 1.12≈0.05,lg 1.3≈0.11,lg 2≈0.30)
A.2021年 B.2022年 C.2023年 D.2024年
C
B
随堂小测
BD
B
A
ACD
A
谢 谢!
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
