中心对称[上学期]

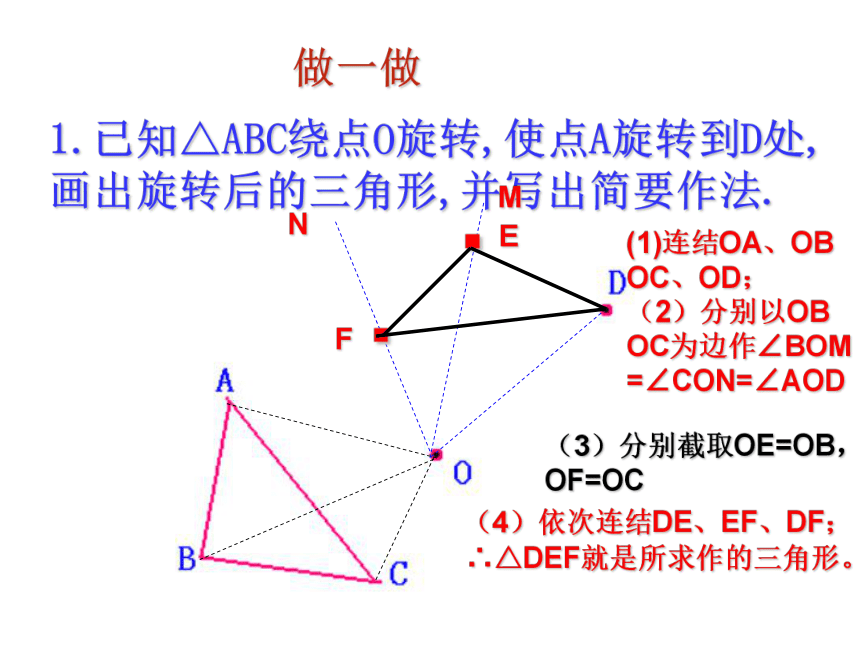
课件17张PPT。23.2.1 中心对称做一做1.已知△ABC绕点O旋转,使点A旋转到D处,
画出旋转后的三角形,并写出简要作法.MN..EF(1)连结OA、OB
OC、OD；
（2）分别以OB
OC为边作∠BOM
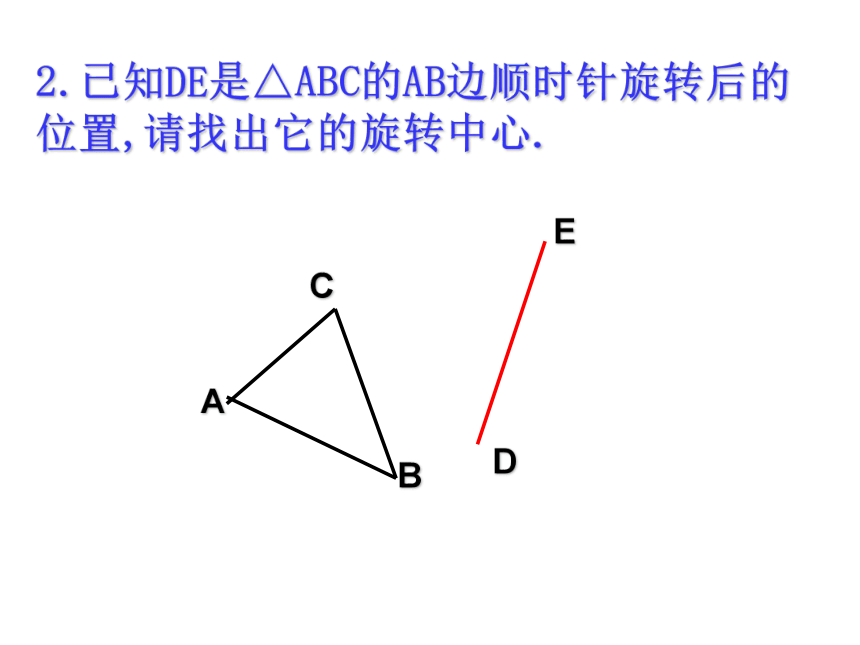
=∠CON=∠AOD（3）分别截取OE=OB，OF=OC（4）依次连结DE、EF、DF；∴△DEF就是所求作的三角形。2.已知DE是△ABC的AB边顺时针旋转后的
位置,请找出它的旋转中心.CDBEA(1)把其中一个图案绕点O旋转180°,你有什么发现?
(2)线段AC,BD相交于点O,OA=OC,OB=OD.把△OCD
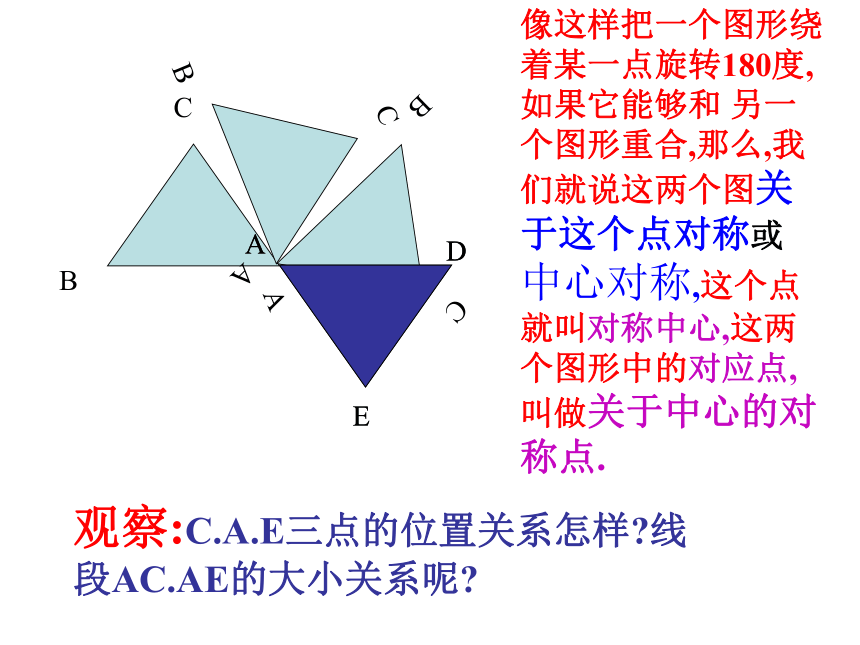
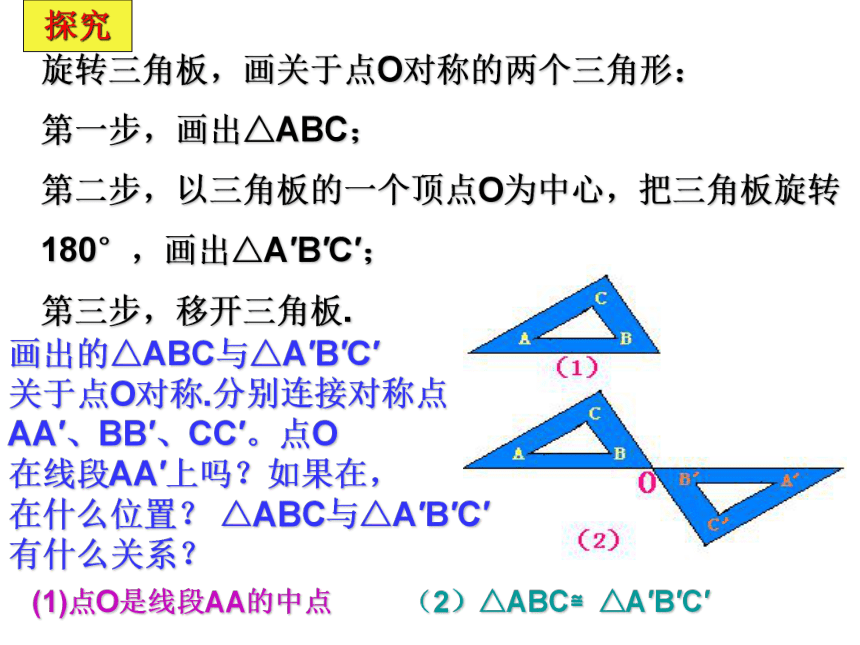
绕点O旋转180°,你有什么发现?重合重合观察像这样把一个图形绕着某一点旋转180度,如果它能够和 另一个图形重合,那么,我们就说这两个图关于这个点对称或中心对称,这个点就叫对称中心,这两个图形中的对应点,叫做关于中心的对称点.观察:C.A.E三点的位置关系怎样?线段AC.AE的大小关系呢?探究旋转三角板，画关于点O对称的两个三角形：
第一步，画出△ABC；
第二步，以三角板的一个顶点O为中心，把三角板旋转
180°，画出△A′B′C′；
第三步，移开三角板.画出的△ABC与△A′B′C′
关于点O对称.分别连接对称点
AA′、BB′、CC′。点O
在线段AA′上吗？如果在，
在什么位置？ △ABC与△A′B′C′
有什么关系？(1)点O是线段AA的中点（2）△ABC≌△A′B′C′下图中△A′B′C′与△ABC关于点O是成中心对称的,你能从图中找到哪些等量关系?探索:(1)OA=OA′、OB=OB′、 OC=OC′（2）△ABC≌△A′B′C′点A绕中心点O旋转180后到点A′，于是A、O、A′三点在一直线上，并且AO＝OA′，另分别在一直线上的三点还有__________，______；并且BO＝______，CO＝______。 B、O、B’Ｃ、Ｏ、Ｃ’ＢＯ’ＣＯ’归纳： （1）在成中心对称的两个图形中,连接对称点的线段都经过对称中心,并且被对称中心平分.
反过来,如果两个图形的对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形一定关于这一点成中心对称.
（2）关于中心对称的两个图形是全等形。都是一个图形和另一个图形重合。有一个对称
中心——点有一条对称轴——直线图形绕中心旋转180°图形沿轴对折你能说出轴对称图形与中心对称图形异同′例1 （1）如图23.2-4,选择点O为对称中心,画出
点O的对称点A′;
(2)如图23.2-5,选择点O为对称中心,画出与
△ABC关于点O对称的△A′B′C′.解:AOA′(1)所以点A′为所求A′C′B′(2) 所以△A′B′C′为所求 如图，已知△ABC与△A’B’C’中心对称，求出它们的对称中心O。应用解法一：根据观察，B、B’应是对应点，连结BB’，用刻度尺找出BB’的中点O，则点O即为所求（如图）OO解法二：根据观察，B、B’及C、C’应是两组对应点，连结BB’、CC’，BB’、CC’相交于点O，则点O即为所求（如图）。
练习P70. 1. 2
P74. 1再见