冀教版数学八年级上册17.3勾股定理(3) 课件(共22张PPT)
文档属性
| 名称 | 冀教版数学八年级上册17.3勾股定理(3) 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 728.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-06 11:46:17 | ||
图片预览







文档简介
(共22张PPT)
勾股定理
学习目标:
1、掌握勾股定理及其证法
2、经历探究和验证勾股定理的过程,发展对图形性质和数量关系猜想和检验的能力
3、体会拼图验证的合理性
4、勾股定理的简单应用
故事分享:
在西方,勾股定理最开始是由毕达哥拉斯提出的,所以又称毕达哥拉斯定理。
更早地,在中国,就记载着商高关于勾股形问题对周公的谈话:“故折矩以为勾广三,股修四,径隅五。”
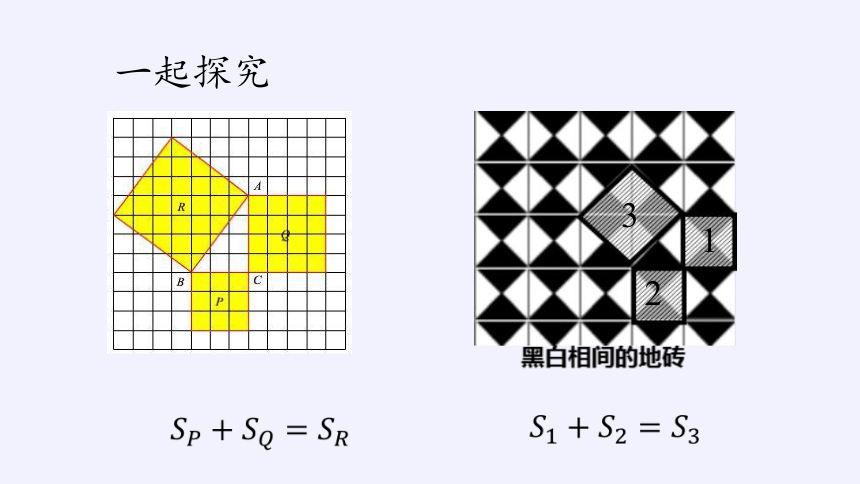
一起探究:
1
3
2
实验
请你猜想:
1、正方形的面积之间有什么样的关系?
2、你能用Rt▲ABC的边把这种关系表示出来吗?
探究可知:
在直角三角形中,两条直角边的平方和等于斜边的平方.
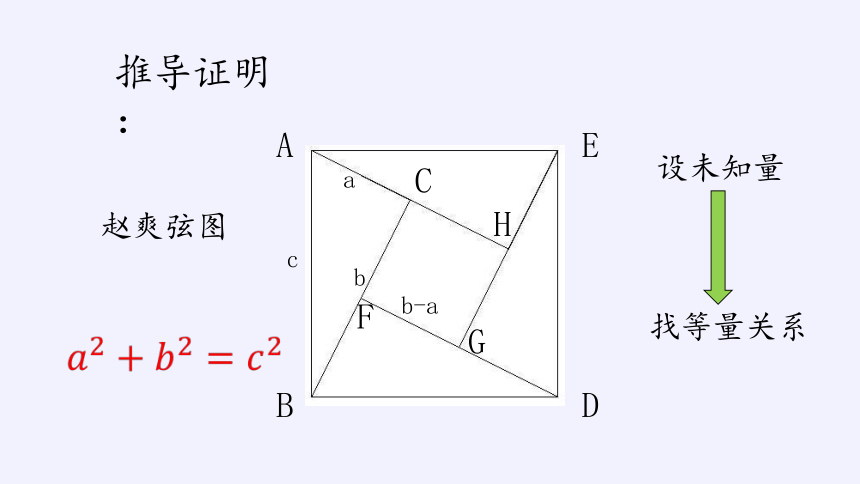
推导证明:
D
A
E
B
G
F
H
C
c
b
a
b-a
赵爽弦图
设未知量
找等量关系
代数证法
总统法
勾股定理:
也可叙述为:
直角三角形两直角边的平方和等于斜边的平方.
弦(c)
A
勾(a)
股(b)
B
C
验证
定理
1
2
C
A
B
O
B
C
A
重要性
几何
代数
勾股定理
结论变形:
课堂检测:
1、已知Rt▲ABC中,直角边a=5,b=12,斜边为c=
2、已知Rt▲ABC中,直角边a=3m,b=4m,斜边为c=
课堂检测:
3、已知Rt▲ABC中,a=2,b=5,c=
①当a和b均为直角边时
②当a为直角边,b为斜边时
课堂小结
毕达哥拉斯树
常见的勾股数大礼包
3 4 5
5 12 13
7 24 25
8 15 17
9 40 41
12 35 37
课后作业
P152 练习 1
A 组 1,3
B 组 1
谢 谢
勾股定理
学习目标:
1、掌握勾股定理及其证法
2、经历探究和验证勾股定理的过程,发展对图形性质和数量关系猜想和检验的能力
3、体会拼图验证的合理性
4、勾股定理的简单应用
故事分享:
在西方,勾股定理最开始是由毕达哥拉斯提出的,所以又称毕达哥拉斯定理。
更早地,在中国,就记载着商高关于勾股形问题对周公的谈话:“故折矩以为勾广三,股修四,径隅五。”
一起探究:
1
3
2
实验
请你猜想:
1、正方形的面积之间有什么样的关系?
2、你能用Rt▲ABC的边把这种关系表示出来吗?
探究可知:
在直角三角形中,两条直角边的平方和等于斜边的平方.
推导证明:
D
A
E
B
G
F
H
C
c
b
a
b-a
赵爽弦图
设未知量
找等量关系
代数证法
总统法
勾股定理:
也可叙述为:
直角三角形两直角边的平方和等于斜边的平方.
弦(c)
A
勾(a)
股(b)
B
C
验证
定理
1
2
C
A
B
O
B
C
A
重要性
几何
代数
勾股定理
结论变形:
课堂检测:
1、已知Rt▲ABC中,直角边a=5,b=12,斜边为c=
2、已知Rt▲ABC中,直角边a=3m,b=4m,斜边为c=
课堂检测:
3、已知Rt▲ABC中,a=2,b=5,c=
①当a和b均为直角边时
②当a为直角边,b为斜边时
课堂小结
毕达哥拉斯树
常见的勾股数大礼包
3 4 5
5 12 13
7 24 25
8 15 17
9 40 41
12 35 37
课后作业
P152 练习 1
A 组 1,3
B 组 1
谢 谢
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
