3.4.1相似三角形的判定(1)课件(共24张PPT)
文档属性
| 名称 | 3.4.1相似三角形的判定(1)课件(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 975.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-08 00:00:00 | ||
图片预览






文档简介
(共24张PPT)
3.4.1 相似三角形的判定(1)
湘教版九年级上册
教学目标
1. 能探究得出“平行于三角形一边的直线与其他两边相交,
截得的三角形与原三角形相似”的结论.
2. 能准确理解两个三角形相似的条件,为以后学习相似三
角形的判定定理打下基础.
3. 能根据上述结论,利用平行线证明两个三角形相似.
4. 锻炼看图能力,发展逻辑思维能力和几何语言表达能力.
温故知新
1. 什么叫作全等三角形?全等三角形有什么性质?
经过图形变换,能够完全重合的两个三角形叫作全等三
角形.全等三角形的对应角相等,对应边也相等.
SAS、ASA、AAS、SSS.对于直角三角形的判定还有“HL”定理.
2. 三角形全等的判定定理有哪些?
温故知新
3. 什么叫作相似三角形?什么叫作相似三角形的相似比?
三个角对应相等,且三条边应边成比例的两个三角形叫作相似三角形.相似三角形的对应边的比叫作相比.
4. 两条直线被一组平行线所截,所得的对应线段 .平行于三角形一边的直线截其他两边,所得的 成比例.
成比例
对应线段
温故知新
在八年级上册,我们已经探讨了两个三角形全等的条件,下面我们来探讨两个三角形相似的条件.为了研究满足什么条件的两个三角形相似,我们先来研究下述问题.
新知讲解
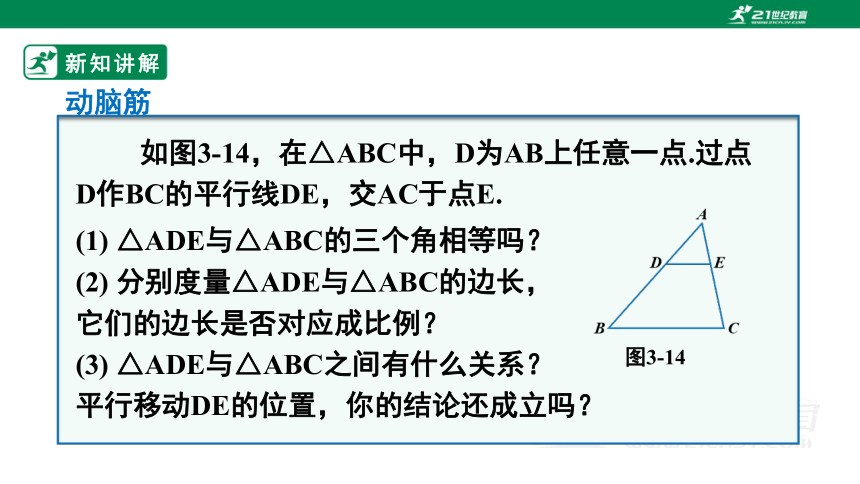
如图3-14,在△ABC中,D为AB上任意一点.过点D作BC的平行线DE,交AC于点E.
动脑筋
(1) △ADE与△ABC的三个角相等吗?
(2) 分别度量△ADE与△ABC的边长,它们的边长是否对应成比例?
(3) △ADE与△ABC之间有什么关系?平行移动DE的位置,你的结论还成立吗?
图3-14
新知讲解
我发现只要DE∥BC,那么△ADE与△ABC是相似的.
如何证明△ADE∽△ABC呢?
根据相似三角形的定义,我们需要证明这两个三角形的三个角对应相等且三条边成比例.上述图中DE∥BC满足说明两个三角形相似的条件吗?
新知讲解
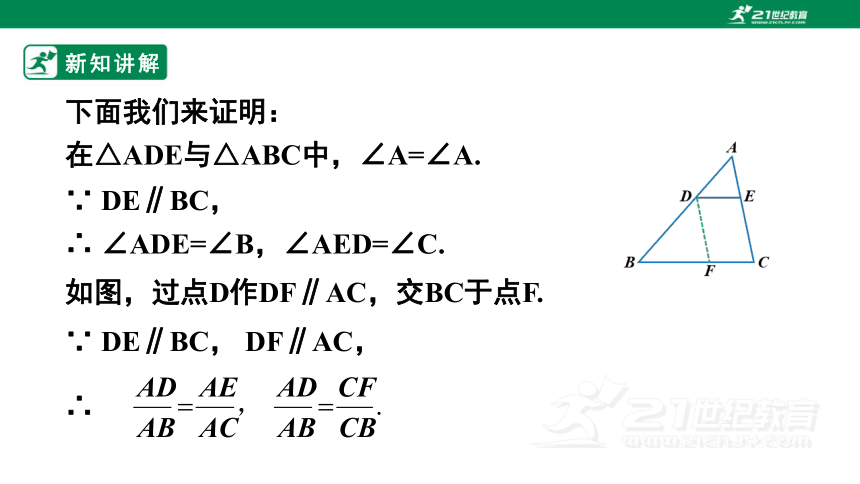
下面我们来证明:
在△ADE与△ABC中,∠A=∠A.
∴ ∠ADE=∠B,∠AED=∠C.
∵ DE∥BC,
如图,过点D作DF∥AC,交BC于点F.
∵ DE∥BC, DF∥AC,
∴
新知讲解
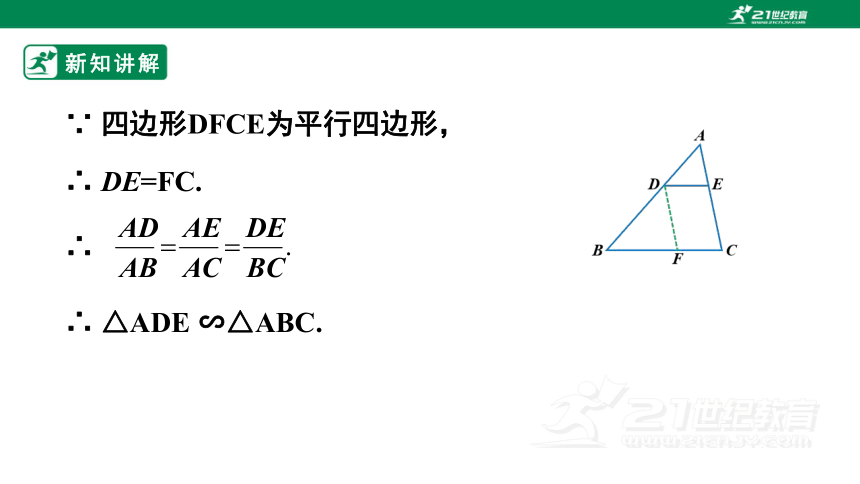
∵ 四边形DFCE为平行四边形,
∴
∴ △ADE ∽△ABC.
∴ DE=FC.
新知讲解
由此得到如下结论:
平行于三角形一边的直线与其他两边相交,截得的三角形与原三角形相似.
例题教学
例1 如图3-16,在△ABC中,已知点D,E分别是AB,AC边的中点.
求证:△ADE∽△ABC.
图3-16
A
B
C
D
E
分析 要证△ADE∽△ABC,根据上述结论,只需证明DE∥BC.
例题教学
证明 ∵点D,E分别是AB,AC边的中点,
∴ DE∥BC.
例1 如图3-16,在△ABC中,已知点D,E分别是AB,AC边的中点.
求证:△ADE∽△ABC.
∴ △ADE∽△ABC.
例题教学
思路 先证△ADE≌△CFE,再证△ADE∽△ABC,
即可证△CFE∽△ABC.
例2 如图3-17,点D为△ABC的边AB的中点,过点D作DE∥BC,交边AC于点E.延长DE至点F,使DE=EF.
求证:△CFE∽△ABC.
例题教学
证明 ∵点D,E分别是AB,AC边的中点,
∴ AE=CE.
∴ △ADE≌△CFE.
图3-17
A
B
C
D
E
F
又 DE=EF,∠AED=∠CEF.
∵ DE∥BC.
∴ △ADE∽△ABC.
∴ △CFE∽△ABC.
课堂总结
1、用平行线判定三角形相似的依据是什么?
平行于三角形一边的直线与其他两边相交,截得的三
角形与原三角形相似.
2、判定两个三角形相似的条件是什么?
通过平移、旋转、轴反射等图形变换,如果能把两个三角形一个角的顶点及两边重合,而另一边恰好平行,那么这两个三角形相似.
课堂练习
1. 如图,在△ABC中,DE∥BC,AD∶AB=1∶3,BC=12,
则DE的长是( )
A. 3 B. 4
C. 5 D. 6
B
解析:根据“平行于三角形一边的直线与其他两边相交,截得的三角形与原三角形相似”,可得△ADE∽△ABC.再根据相似三角形的性质列出比例式,即可求出DE的长.
A
B
C
D
E
课堂练习
2. (易错题)如图,在△ABC中,DE∥BC,AD∶DB=1∶3,
BC=12, 则DE的长是( )
A. 3 B. 4
C. 5 D. 6
A
解析:本题与第1题不同之处是,AD∶DB=1∶3不是△ADE与△ABC的对应边的比,应先求出对应边的比AD∶AB=1∶4,再用相似三角形法性质即得所要的选项.
A
B
C
D
E
课堂练习
3. 在平行四边形ABCD中,对角线AC=15,BC=12,点E是AC的三等分点,AM=2.5,则BN=( )
A. 5 B. 6
C. 7 D. 8
提示:先判定△AEM∽△CEN,根据“相似三角形是对应边成比例”列比例式求出CN=5,即可求出BN=7,故选C.
C
板书设计
相似三角形的判定(1)
1. 平行于三角形一边的直线与其他两边相交,截得的三角
形与原三角形相似.
2. 证明两个三角形相似,可以解决求有关角与边的问题.
作业布置
第78、79页课后练习第1、2题
1.如图,在Rt△ABC中,∠C=90°.正方形EFCD的三个顶点E,F,D分别在边AB,BC,AC上.已知AC=7.5,BC=5,求正方形的边长.
解:∵ ∠C=90°,四边形EFCD正方形,CD在AC上,
∴ ED∥BC.
∴△AED∽△ABC.
作业布置
设正方形的边长为x,则ED=DC=x,
AD=AC-DC=7.5-x.又BC=5,于是有
解得 x=3,即正方形为3.
作业布置
2. 如图,已知点O在四边形ABCD的对角线AC上,OE∥CB,OF∥CD.试判断四边形AEOF与四边形ABCD是否相似,并说明理由.
提示:要判定四边形AEOF与四边形ABCD相似,就要先证明它们的对应角相等,对应边成比例.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
3.4.1 相似三角形的判定(1)
湘教版九年级上册
教学目标
1. 能探究得出“平行于三角形一边的直线与其他两边相交,
截得的三角形与原三角形相似”的结论.
2. 能准确理解两个三角形相似的条件,为以后学习相似三
角形的判定定理打下基础.
3. 能根据上述结论,利用平行线证明两个三角形相似.
4. 锻炼看图能力,发展逻辑思维能力和几何语言表达能力.
温故知新
1. 什么叫作全等三角形?全等三角形有什么性质?
经过图形变换,能够完全重合的两个三角形叫作全等三
角形.全等三角形的对应角相等,对应边也相等.
SAS、ASA、AAS、SSS.对于直角三角形的判定还有“HL”定理.
2. 三角形全等的判定定理有哪些?
温故知新
3. 什么叫作相似三角形?什么叫作相似三角形的相似比?
三个角对应相等,且三条边应边成比例的两个三角形叫作相似三角形.相似三角形的对应边的比叫作相比.
4. 两条直线被一组平行线所截,所得的对应线段 .平行于三角形一边的直线截其他两边,所得的 成比例.
成比例
对应线段
温故知新
在八年级上册,我们已经探讨了两个三角形全等的条件,下面我们来探讨两个三角形相似的条件.为了研究满足什么条件的两个三角形相似,我们先来研究下述问题.
新知讲解
如图3-14,在△ABC中,D为AB上任意一点.过点D作BC的平行线DE,交AC于点E.
动脑筋
(1) △ADE与△ABC的三个角相等吗?
(2) 分别度量△ADE与△ABC的边长,它们的边长是否对应成比例?
(3) △ADE与△ABC之间有什么关系?平行移动DE的位置,你的结论还成立吗?
图3-14
新知讲解
我发现只要DE∥BC,那么△ADE与△ABC是相似的.
如何证明△ADE∽△ABC呢?
根据相似三角形的定义,我们需要证明这两个三角形的三个角对应相等且三条边成比例.上述图中DE∥BC满足说明两个三角形相似的条件吗?
新知讲解
下面我们来证明:
在△ADE与△ABC中,∠A=∠A.
∴ ∠ADE=∠B,∠AED=∠C.
∵ DE∥BC,
如图,过点D作DF∥AC,交BC于点F.
∵ DE∥BC, DF∥AC,
∴
新知讲解
∵ 四边形DFCE为平行四边形,
∴
∴ △ADE ∽△ABC.
∴ DE=FC.
新知讲解
由此得到如下结论:
平行于三角形一边的直线与其他两边相交,截得的三角形与原三角形相似.
例题教学
例1 如图3-16,在△ABC中,已知点D,E分别是AB,AC边的中点.
求证:△ADE∽△ABC.
图3-16
A
B
C
D
E
分析 要证△ADE∽△ABC,根据上述结论,只需证明DE∥BC.
例题教学
证明 ∵点D,E分别是AB,AC边的中点,
∴ DE∥BC.
例1 如图3-16,在△ABC中,已知点D,E分别是AB,AC边的中点.
求证:△ADE∽△ABC.
∴ △ADE∽△ABC.
例题教学
思路 先证△ADE≌△CFE,再证△ADE∽△ABC,
即可证△CFE∽△ABC.
例2 如图3-17,点D为△ABC的边AB的中点,过点D作DE∥BC,交边AC于点E.延长DE至点F,使DE=EF.
求证:△CFE∽△ABC.
例题教学
证明 ∵点D,E分别是AB,AC边的中点,
∴ AE=CE.
∴ △ADE≌△CFE.
图3-17
A
B
C
D
E
F
又 DE=EF,∠AED=∠CEF.
∵ DE∥BC.
∴ △ADE∽△ABC.
∴ △CFE∽△ABC.
课堂总结
1、用平行线判定三角形相似的依据是什么?
平行于三角形一边的直线与其他两边相交,截得的三
角形与原三角形相似.
2、判定两个三角形相似的条件是什么?
通过平移、旋转、轴反射等图形变换,如果能把两个三角形一个角的顶点及两边重合,而另一边恰好平行,那么这两个三角形相似.
课堂练习
1. 如图,在△ABC中,DE∥BC,AD∶AB=1∶3,BC=12,
则DE的长是( )
A. 3 B. 4
C. 5 D. 6
B
解析:根据“平行于三角形一边的直线与其他两边相交,截得的三角形与原三角形相似”,可得△ADE∽△ABC.再根据相似三角形的性质列出比例式,即可求出DE的长.
A
B
C
D
E
课堂练习
2. (易错题)如图,在△ABC中,DE∥BC,AD∶DB=1∶3,
BC=12, 则DE的长是( )
A. 3 B. 4
C. 5 D. 6
A
解析:本题与第1题不同之处是,AD∶DB=1∶3不是△ADE与△ABC的对应边的比,应先求出对应边的比AD∶AB=1∶4,再用相似三角形法性质即得所要的选项.
A
B
C
D
E
课堂练习
3. 在平行四边形ABCD中,对角线AC=15,BC=12,点E是AC的三等分点,AM=2.5,则BN=( )
A. 5 B. 6
C. 7 D. 8
提示:先判定△AEM∽△CEN,根据“相似三角形是对应边成比例”列比例式求出CN=5,即可求出BN=7,故选C.
C
板书设计
相似三角形的判定(1)
1. 平行于三角形一边的直线与其他两边相交,截得的三角
形与原三角形相似.
2. 证明两个三角形相似,可以解决求有关角与边的问题.
作业布置
第78、79页课后练习第1、2题
1.如图,在Rt△ABC中,∠C=90°.正方形EFCD的三个顶点E,F,D分别在边AB,BC,AC上.已知AC=7.5,BC=5,求正方形的边长.
解:∵ ∠C=90°,四边形EFCD正方形,CD在AC上,
∴ ED∥BC.
∴△AED∽△ABC.
作业布置
设正方形的边长为x,则ED=DC=x,
AD=AC-DC=7.5-x.又BC=5,于是有
解得 x=3,即正方形为3.
作业布置
2. 如图,已知点O在四边形ABCD的对角线AC上,OE∥CB,OF∥CD.试判断四边形AEOF与四边形ABCD是否相似,并说明理由.
提示:要判定四边形AEOF与四边形ABCD相似,就要先证明它们的对应角相等,对应边成比例.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
