3.4.2相似三角形的性质(1)课件课件(共25张PPT)
文档属性
| 名称 | 3.4.2相似三角形的性质(1)课件课件(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-08 09:25:46 | ||
图片预览






文档简介
(共25张PPT)
3.4.2 相似三角形的性质(1)
湘教版九年级上册
教学目标
1. 能理解并记住相似三角形的性质:相似三角形的对应高
的比等于相似比.
2. 能证明并记住相似三角形的性质:相似三角形的对应角
平分线的比等于相似比,对应中线的比等于相似比.
3. 能运用相似三角形的上述性质求相关线段的长.
4. 培养学生的看图用图能力、逻辑推理能力和计算能力.
课堂总结
1. 判定三角形相似有哪些方法?
平行于三角形一边的直线与其他两边相交,截得的三角形与原三角形相似.
相似三角形的判定定理1:两角相等的两个三角形相似.
相似三角形的判定定理2:两边成比例且夹角相等的两个三角形相似.
相似三角形的判定定理3:三边成比例的两个三角形相似.
温故知新
2. 相似三角形的角和边有什么性质?
相似三角形的对应角相等,对应边成比例.
两个三角形相似,除了它们的对应角相等,对应边成
比例外,相似三角形还有哪些性质呢?
新知讲解
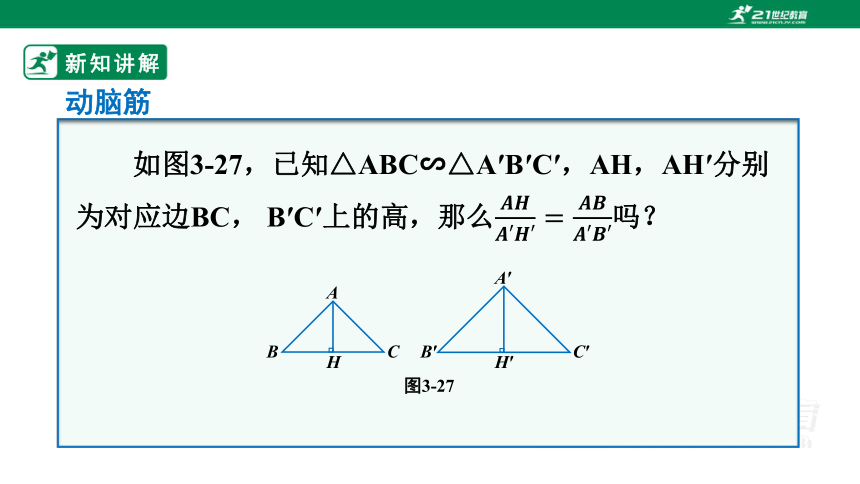
如图3-27,已知△ABC∽△A′B′C′,AH,AH′分别为对应边BC, B′C′上的高,那么吗?
动脑筋
图3-27
A
C
A′
C′
B′
H′
B
H
新知讲解
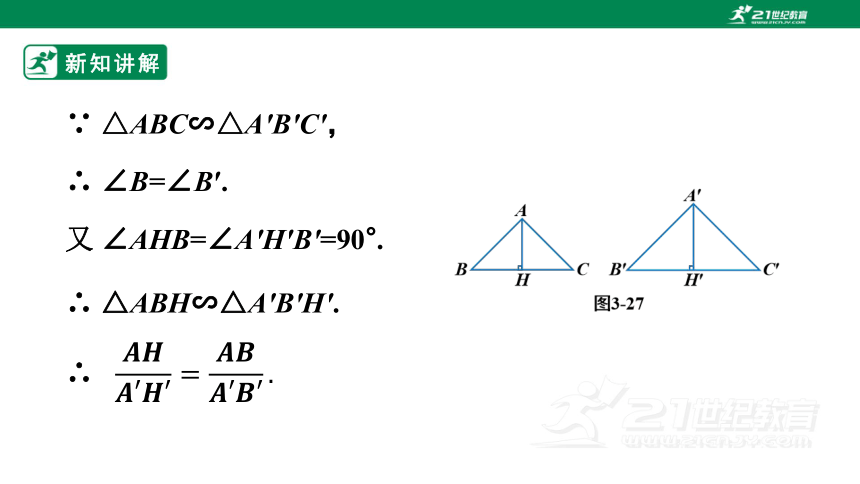
∵ △ABC∽△A′B′C′,
∴ △ABH∽△A′B′H′.
∴ ∠B=∠B′.
又 ∠AHB=∠A′H′B′=90°.
∴
新知讲解
相似三角形对应高的比等于相似比.
类似地,我们可以得到其余两组对应边上的高的比也等于相似比.由此得到:
例题教学
例9 如图3-28,AB∥PQ,AB=,PQ=120m,点P,A,C在一条直线上,点Q,B,C也在一条直线上,若AB与PQ的直线距离是40m,求点C到直线PQ的距离.
分析 由AB∥PQ可证△ABC∽△PQC,再根据相似三角形的对应高的比等于相似比的性质,即可求出点C到直线PQ的距离.
例题教学
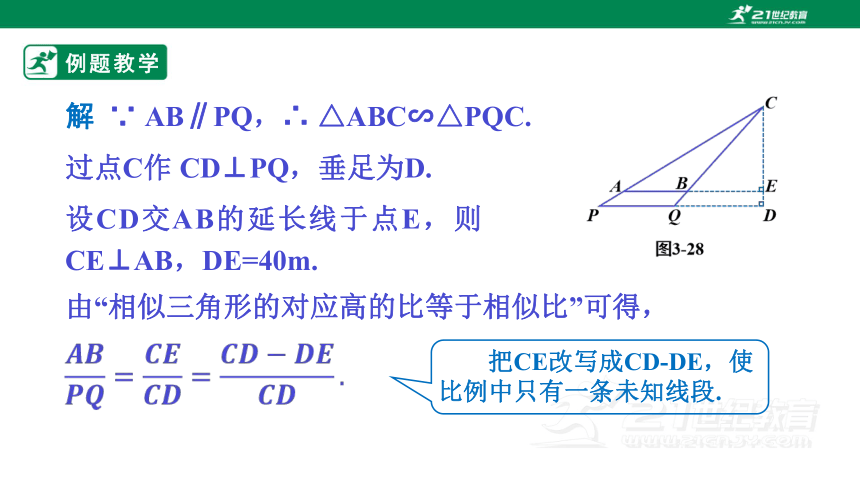
解 ∵ AB∥PQ,∴ △ABC∽△PQC.
过点C作 CD⊥PQ,垂足为D.
由“相似三角形的对应高的比等于相似比”可得,
设CD交AB的延长线于点E,则CE⊥AB,DE=40m.
把CE改写成CD-DE,使比例中只有一条未知线段.
例题教学
又 AB=,PQ=120m,DE=40m,
答:点C到直线PQ的距离是240m.
∴ CD=240m.
例题教学
分析 因为结论中的AT,AB,AT′,A′B′分别为△ABT和△A′B′T′的边,所以需先证△ABT∽△A′B′T′.
例10 如图3-29,已知△ABC∽△A′B′C′,AT,AT′分别为对应角∠BAC,∠B′A′C′的平分线.
求证:
A
B
C
A′
B′
C′
T′
T
图3-29
例题教学
证明 ∵△ABC∽△A′B′C′,
∴ ∠B=∠B′,∠BAC=∠B′A′C′.
∴ △ADE∽△ABC.
又 AT,AT′分别为∠BAC,∠B′A′C′的平分线.
∴ ∠BAT=∠BAC=∠B′A′C′=∠B′A′T′.
∴ △ABT∽△A′B′T′.
例题教学
相似三角形对应的角平分线的比等于相似比.
类似地,我们可以得到其余两组对应角平分线的比也等于相似比.由此得到:
合作探究
已知△ABC∽△A′B′C′,若AD,AD′分别为
△BAC,△B′A′C′的中线,则成立吗?
由此你能得到什么结论?
A
B
C
A′
B′
C′
D′
D
议一议
例题教学
相似三角形对应边上的中线的比等于相似比.
我们可以仿照例9的方法证明成立,类似地,我们也能得到其余两组对应边的中线的比等于相似比.
由此得到:
课堂总结
今天我们学了相似三角形的哪些性质?
相似三角形对应高的比等于相似比.
相似三角形对应的角平分线的比等于相似比.
相似三角形对应边上的中线的比等于相似比.
课堂练习
1. 已知△ABC∽△DEF,相似比为2∶3,则对应高的比是( )
A. 2∶3 B. 2∶5
C. 5∶3 D. 5∶6
A
课堂练习
2. 已知△ABC∽△DEF的对应高的比为5∶6,则对应中线
的比是( )
A. 4∶5 B. 5∶6
C. 6∶5 D. 8∶11
B
课堂练习
3. 如图,在△ABC中,DE∥BC,AH⊥BC与点H,交DE于点F,AH=12,=,则DE到BC的距离是( )
A. 6
B. 8
C. 9
D. 10
C
课堂练习
4. 如图,△ABC∽△BDC,E,F分别是AC,BC的中点,AC=12,BC=8,BE=6,则DF的长为( )
A. 4 B. 5
C. 6 D. 8
A
A
B
C
D
E
F
板书设计
相似三角形的性质(1)
1. 相似三角形的对应角相等,对应边成比例;相似三角形
对应的高、角平分线和中线的比等于相似比.
2. 利用相似三角形的性质,求有关角与边以及对应边上的
高、中线以及对应的角平分线.
作业布置
第87页课后练习第1、2题
1. 已知△ABC∽△DEF,AM,DN分别为△ABC, △DEF的一条中线,且AM=6cm,AB=8cm,DE=4cm,求DN的长.
作业布置
2. 如图,△ABC∽△A′B′C′,AD,BE分别是△ABC的高和中线,A′D′,B′E′分别是△A′B′C′的高和中线,且AD=4,A′D′=3,BE=6,求B′E′的长.
B
C
A
D
E
B′
C′
A′
D′
E′
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
3.4.2 相似三角形的性质(1)
湘教版九年级上册
教学目标
1. 能理解并记住相似三角形的性质:相似三角形的对应高
的比等于相似比.
2. 能证明并记住相似三角形的性质:相似三角形的对应角
平分线的比等于相似比,对应中线的比等于相似比.
3. 能运用相似三角形的上述性质求相关线段的长.
4. 培养学生的看图用图能力、逻辑推理能力和计算能力.
课堂总结
1. 判定三角形相似有哪些方法?
平行于三角形一边的直线与其他两边相交,截得的三角形与原三角形相似.
相似三角形的判定定理1:两角相等的两个三角形相似.
相似三角形的判定定理2:两边成比例且夹角相等的两个三角形相似.
相似三角形的判定定理3:三边成比例的两个三角形相似.
温故知新
2. 相似三角形的角和边有什么性质?
相似三角形的对应角相等,对应边成比例.
两个三角形相似,除了它们的对应角相等,对应边成
比例外,相似三角形还有哪些性质呢?
新知讲解
如图3-27,已知△ABC∽△A′B′C′,AH,AH′分别为对应边BC, B′C′上的高,那么吗?
动脑筋
图3-27
A
C
A′
C′
B′
H′
B
H
新知讲解
∵ △ABC∽△A′B′C′,
∴ △ABH∽△A′B′H′.
∴ ∠B=∠B′.
又 ∠AHB=∠A′H′B′=90°.
∴
新知讲解
相似三角形对应高的比等于相似比.
类似地,我们可以得到其余两组对应边上的高的比也等于相似比.由此得到:
例题教学
例9 如图3-28,AB∥PQ,AB=,PQ=120m,点P,A,C在一条直线上,点Q,B,C也在一条直线上,若AB与PQ的直线距离是40m,求点C到直线PQ的距离.
分析 由AB∥PQ可证△ABC∽△PQC,再根据相似三角形的对应高的比等于相似比的性质,即可求出点C到直线PQ的距离.
例题教学
解 ∵ AB∥PQ,∴ △ABC∽△PQC.
过点C作 CD⊥PQ,垂足为D.
由“相似三角形的对应高的比等于相似比”可得,
设CD交AB的延长线于点E,则CE⊥AB,DE=40m.
把CE改写成CD-DE,使比例中只有一条未知线段.
例题教学
又 AB=,PQ=120m,DE=40m,
答:点C到直线PQ的距离是240m.
∴ CD=240m.
例题教学
分析 因为结论中的AT,AB,AT′,A′B′分别为△ABT和△A′B′T′的边,所以需先证△ABT∽△A′B′T′.
例10 如图3-29,已知△ABC∽△A′B′C′,AT,AT′分别为对应角∠BAC,∠B′A′C′的平分线.
求证:
A
B
C
A′
B′
C′
T′
T
图3-29
例题教学
证明 ∵△ABC∽△A′B′C′,
∴ ∠B=∠B′,∠BAC=∠B′A′C′.
∴ △ADE∽△ABC.
又 AT,AT′分别为∠BAC,∠B′A′C′的平分线.
∴ ∠BAT=∠BAC=∠B′A′C′=∠B′A′T′.
∴ △ABT∽△A′B′T′.
例题教学
相似三角形对应的角平分线的比等于相似比.
类似地,我们可以得到其余两组对应角平分线的比也等于相似比.由此得到:
合作探究
已知△ABC∽△A′B′C′,若AD,AD′分别为
△BAC,△B′A′C′的中线,则成立吗?
由此你能得到什么结论?
A
B
C
A′
B′
C′
D′
D
议一议
例题教学
相似三角形对应边上的中线的比等于相似比.
我们可以仿照例9的方法证明成立,类似地,我们也能得到其余两组对应边的中线的比等于相似比.
由此得到:
课堂总结
今天我们学了相似三角形的哪些性质?
相似三角形对应高的比等于相似比.
相似三角形对应的角平分线的比等于相似比.
相似三角形对应边上的中线的比等于相似比.
课堂练习
1. 已知△ABC∽△DEF,相似比为2∶3,则对应高的比是( )
A. 2∶3 B. 2∶5
C. 5∶3 D. 5∶6
A
课堂练习
2. 已知△ABC∽△DEF的对应高的比为5∶6,则对应中线
的比是( )
A. 4∶5 B. 5∶6
C. 6∶5 D. 8∶11
B
课堂练习
3. 如图,在△ABC中,DE∥BC,AH⊥BC与点H,交DE于点F,AH=12,=,则DE到BC的距离是( )
A. 6
B. 8
C. 9
D. 10
C
课堂练习
4. 如图,△ABC∽△BDC,E,F分别是AC,BC的中点,AC=12,BC=8,BE=6,则DF的长为( )
A. 4 B. 5
C. 6 D. 8
A
A
B
C
D
E
F
板书设计
相似三角形的性质(1)
1. 相似三角形的对应角相等,对应边成比例;相似三角形
对应的高、角平分线和中线的比等于相似比.
2. 利用相似三角形的性质,求有关角与边以及对应边上的
高、中线以及对应的角平分线.
作业布置
第87页课后练习第1、2题
1. 已知△ABC∽△DEF,AM,DN分别为△ABC, △DEF的一条中线,且AM=6cm,AB=8cm,DE=4cm,求DN的长.
作业布置
2. 如图,△ABC∽△A′B′C′,AD,BE分别是△ABC的高和中线,A′D′,B′E′分别是△A′B′C′的高和中线,且AD=4,A′D′=3,BE=6,求B′E′的长.
B
C
A
D
E
B′
C′
A′
D′
E′
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
