3.4.2相似三角形的性质(2)课件(共22张PPT)
文档属性
| 名称 | 3.4.2相似三角形的性质(2)课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-08 10:11:27 | ||
图片预览







文档简介
(共22张PPT)
3.4.2 相似三角形的性质(2)
湘教版九年级上册
教学目标
1. 理解和掌握相似三角形的性质:
相似三角形的面积的比等于相似比的平方.
2. 能推导、记住“相似三角形周长的比等于相似比”的性质.
3. 能灵活运用相似三角形的性质解决问题.
4. 锤炼几何语言表达能力,提高推理能力和学习自信心.
新知导入
我们已经学过的相似三角形的性质有哪些?
②相似三角形对应高、对应中线、对应角平分线的比都等于等于相似比(对应边的比).
①相似三角形的对应角相等,对应边成比例.
相似三角形还有哪些性质呢?
新知讲解
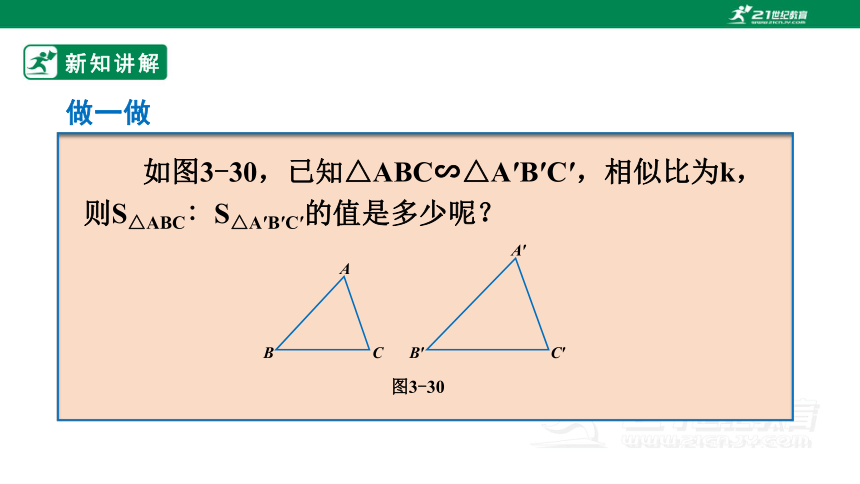
如图3-30,已知△ABC∽△A′B′C′,相似比为k,
则S△ABC∶S△A′B′C′的值是多少呢?
做一做
A
B
C
A′
B′
C′
图3-30
新知讲解
分别作BC,B′C′上的高AD,A′D′,则
因此,
新知讲解
由此得到:
相似三角形的面积比等于相似比的平方.
例题教学
例11 如图,在△ABC中,EF∥BC,,S四边形BCFE=8,
求S△ABC.
思路 先证明△AEF∽△ABC,求出相似比;再根据相似三角形面积的比等于相似比的平方,列式即可求出S△ABC.
A
B
C
E
F
解 ∵ EF∥BC,∴ △AEF∽△ABC.
例题教学
∴
即
例题教学
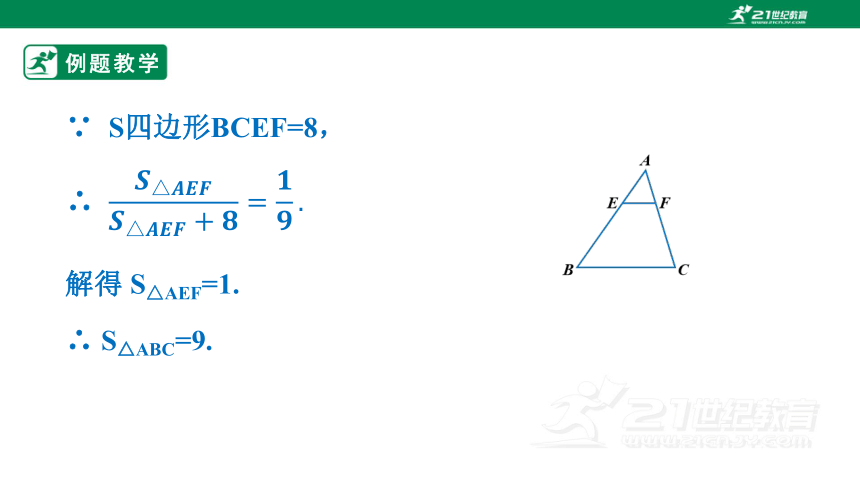
∵ S四边形BCEF=8,
∴
解得 S△AEF=1.
∴ S△ABC=9.
新知讲解
例12 已知△ABC与△A′B′C′的相似比为,且S△ABC +S△A′B′C′=91,求△A′B′C′的面积.
分析 已知△ABC与△A′B′C′的相似比,则可求出两个三角形的面积比,从而得到△ABC与△A′B′C′的面积关系,把这个面积关系代入S△ABC +S△A′B′C′=91即可求出S△A′B′C′.
新知讲解
例12 已知△ABC与△A′B′C′的相似比为,且S△ABC +S△A′B′C′=91,求△A′B′C′的面积.
解 ∵ △ABC与△A′B′C′的相似比为,
即
又 S△ABC +S△A′B′C′=91,
∴
∴ S△A′B′C′=63.
课堂练习
1. 如果两个三角形的边长的比等于2∶3,那么这两个三角形的面积的比是( )
A. 2∶3 B. 4∶9
C. ∶ D. ∶
B
课堂练习
2. 如果两个等边三角形的面积的比等于49∶4,那么这两个等边三角形的周长的比是( )
A. 49∶4 B. 4∶49
C. 7∶ 2 D. 2∶7
C
课堂练习
3. 如图,线段AB,CD相交于点O,且EF∥BC,AO=8,BO=12,若S△AOC=8,则S△BOD=( )
A. 12 B. 16
C. 18 D. 24
C
A
B
C
O
D
课堂练习
4. 如图,把△ABC沿直线平移到△A B C 的位置,使它们的重叠部分(阴影部分)的面积是△ABC的一半,若AB=,则△ABC移动的距离是( )
A. B.
C. 1 D.
B
A
B
C
C
A
B
课堂总结
相似三角形相有哪些性质?
相似三角形的对应角相等,对应边成比例.
相似三角形的对应高、对应中线、对应角平分线以及周长的比等于相似比.一句话,即:相似三角形对应线段的比,周长的比都等于相似比.
相似三角形的面积的比等于相似比的平方.
板书设计
相似三角形的性质(2)
1. 相似三角形的周长的比等于相似比.
2. 相似三角形的面积的比等于相似比的平方.
3. 相似三角形的性质的灵活运用.
作业布置
第89页课后练习第1、2、3题
1. 证明:相似三角形的周长的比等于相似比.
B
C
A
D
E
F
证明:如图,设△ABC∽△DEF,相似比为k,则
AB=kDE,BC=kEF,CA=kFD.
∴
即相似三角形的周长的比等于相似比.
作业布置
2. 已知△ABC∽△A′B′C′,它们的周长分别为60cm和72cm,
且AB=15cm,B′C′=24cm,求BC,AC,A′B′,A′C′的长.
解:∵ 相似三角形的周长的比等于相似比,
∴
∴
AC=60-AB-BC=25cm,A′C′=72-A′B′-B′C′=30cm.
作业布置
3. 有一个直角三角形的边长分别为3,4,5,另一个与它相似的直角三角形的最小边为7,则另一个直角三角形的周长和面积分别是多少?
解:另一个直角三角形的边长与已知三角形的相似比是,故其周长的比是,面积的比是.
则另一个直角三角形的周长是
另一个直角三角形的面积是
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
3.4.2 相似三角形的性质(2)
湘教版九年级上册
教学目标
1. 理解和掌握相似三角形的性质:
相似三角形的面积的比等于相似比的平方.
2. 能推导、记住“相似三角形周长的比等于相似比”的性质.
3. 能灵活运用相似三角形的性质解决问题.
4. 锤炼几何语言表达能力,提高推理能力和学习自信心.
新知导入
我们已经学过的相似三角形的性质有哪些?
②相似三角形对应高、对应中线、对应角平分线的比都等于等于相似比(对应边的比).
①相似三角形的对应角相等,对应边成比例.
相似三角形还有哪些性质呢?
新知讲解
如图3-30,已知△ABC∽△A′B′C′,相似比为k,
则S△ABC∶S△A′B′C′的值是多少呢?
做一做
A
B
C
A′
B′
C′
图3-30
新知讲解
分别作BC,B′C′上的高AD,A′D′,则
因此,
新知讲解
由此得到:
相似三角形的面积比等于相似比的平方.
例题教学
例11 如图,在△ABC中,EF∥BC,,S四边形BCFE=8,
求S△ABC.
思路 先证明△AEF∽△ABC,求出相似比;再根据相似三角形面积的比等于相似比的平方,列式即可求出S△ABC.
A
B
C
E
F
解 ∵ EF∥BC,∴ △AEF∽△ABC.
例题教学
∴
即
例题教学
∵ S四边形BCEF=8,
∴
解得 S△AEF=1.
∴ S△ABC=9.
新知讲解
例12 已知△ABC与△A′B′C′的相似比为,且S△ABC +S△A′B′C′=91,求△A′B′C′的面积.
分析 已知△ABC与△A′B′C′的相似比,则可求出两个三角形的面积比,从而得到△ABC与△A′B′C′的面积关系,把这个面积关系代入S△ABC +S△A′B′C′=91即可求出S△A′B′C′.
新知讲解
例12 已知△ABC与△A′B′C′的相似比为,且S△ABC +S△A′B′C′=91,求△A′B′C′的面积.
解 ∵ △ABC与△A′B′C′的相似比为,
即
又 S△ABC +S△A′B′C′=91,
∴
∴ S△A′B′C′=63.
课堂练习
1. 如果两个三角形的边长的比等于2∶3,那么这两个三角形的面积的比是( )
A. 2∶3 B. 4∶9
C. ∶ D. ∶
B
课堂练习
2. 如果两个等边三角形的面积的比等于49∶4,那么这两个等边三角形的周长的比是( )
A. 49∶4 B. 4∶49
C. 7∶ 2 D. 2∶7
C
课堂练习
3. 如图,线段AB,CD相交于点O,且EF∥BC,AO=8,BO=12,若S△AOC=8,则S△BOD=( )
A. 12 B. 16
C. 18 D. 24
C
A
B
C
O
D
课堂练习
4. 如图,把△ABC沿直线平移到△A B C 的位置,使它们的重叠部分(阴影部分)的面积是△ABC的一半,若AB=,则△ABC移动的距离是( )
A. B.
C. 1 D.
B
A
B
C
C
A
B
课堂总结
相似三角形相有哪些性质?
相似三角形的对应角相等,对应边成比例.
相似三角形的对应高、对应中线、对应角平分线以及周长的比等于相似比.一句话,即:相似三角形对应线段的比,周长的比都等于相似比.
相似三角形的面积的比等于相似比的平方.
板书设计
相似三角形的性质(2)
1. 相似三角形的周长的比等于相似比.
2. 相似三角形的面积的比等于相似比的平方.
3. 相似三角形的性质的灵活运用.
作业布置
第89页课后练习第1、2、3题
1. 证明:相似三角形的周长的比等于相似比.
B
C
A
D
E
F
证明:如图,设△ABC∽△DEF,相似比为k,则
AB=kDE,BC=kEF,CA=kFD.
∴
即相似三角形的周长的比等于相似比.
作业布置
2. 已知△ABC∽△A′B′C′,它们的周长分别为60cm和72cm,
且AB=15cm,B′C′=24cm,求BC,AC,A′B′,A′C′的长.
解:∵ 相似三角形的周长的比等于相似比,
∴
∴
AC=60-AB-BC=25cm,A′C′=72-A′B′-B′C′=30cm.
作业布置
3. 有一个直角三角形的边长分别为3,4,5,另一个与它相似的直角三角形的最小边为7,则另一个直角三角形的周长和面积分别是多少?
解:另一个直角三角形的边长与已知三角形的相似比是,故其周长的比是,面积的比是.
则另一个直角三角形的周长是
另一个直角三角形的面积是
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
