中心对称[上学期]

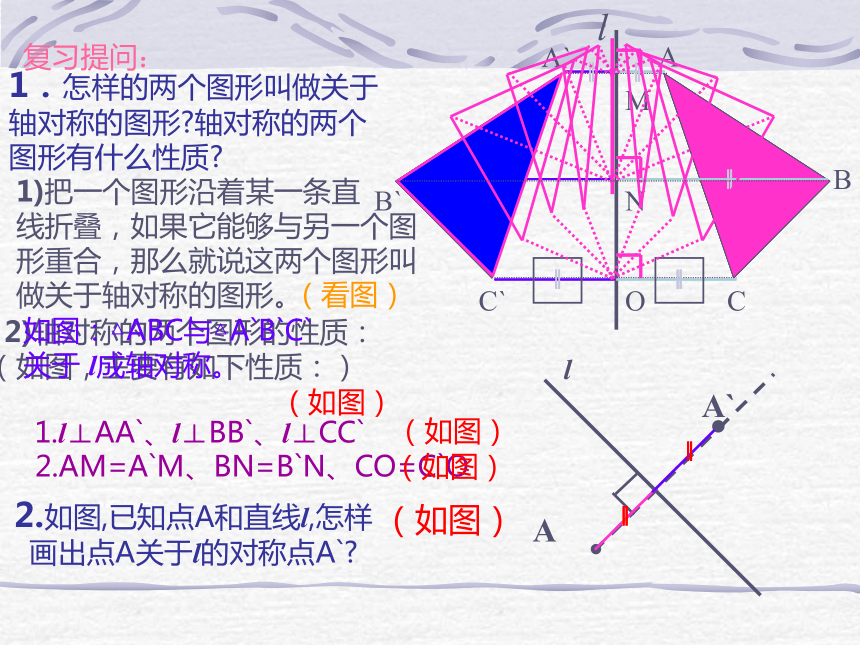
课件18张PPT。中心对称复习提问：1．怎样的两个图形叫做关于轴对称的图形?轴对称的两个图形有什么性质?2.如图,已知点A和直线l,怎样画出点A关于l的对称点A`?（如图）ABCA`C`B`1)把一个图形沿着某一条直
线折叠，如果它能够与另一个图形重合，那么就说这两个图形叫做关于轴对称的图形。 2)轴对称的两个图形的性质：
（如图，主要有如下性质：）1.l⊥AA`、l⊥BB`、l⊥CC`MNO2.AM=A`M、BN=B`N、CO=C`O（如图）（如图）（如图）如图：△ABC与△A`B`C`
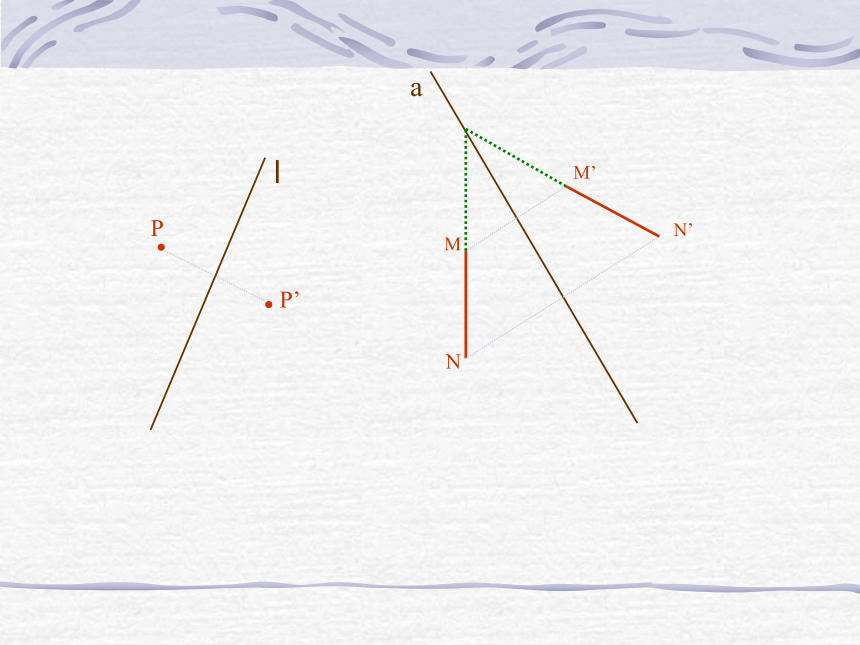
关于 l成轴对称。l（看图）PlaMNP’M’N’怎样的两个图形叫做关于某直线成轴对称？成轴对称
的两个图形有什么性质？定义三要点性 质1 2 3有一条轴对称——直线图形沿轴对折，即翻转180°翻转后与另一图形重合1 2 3轴 对 称两个图形是全等形对称轴是对应点连线的垂直平分线对应线段或延长线相交，交点在
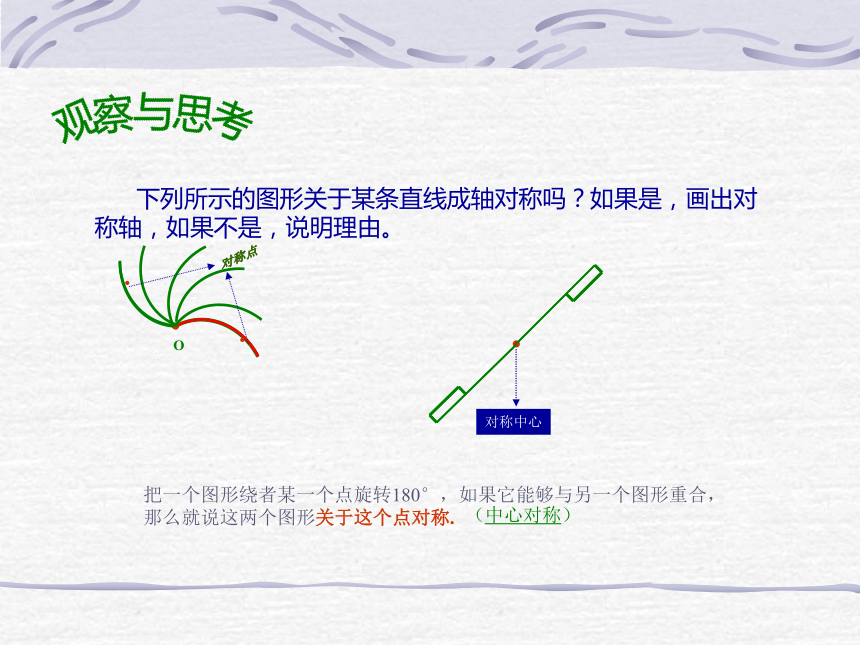
对称轴上观察与思考 下列所示的图形关于某条直线成轴对称吗？如果是，画出对
称轴，如果不是，说明理由。
O对称中心把一个图形绕者某一个点旋转180°，如果它能够与另一个图形重合，
那么就说这两个图形关于这个点对称.（中心对称）对称点 两个图形关于点对称也
称中心对称。这两个图形中
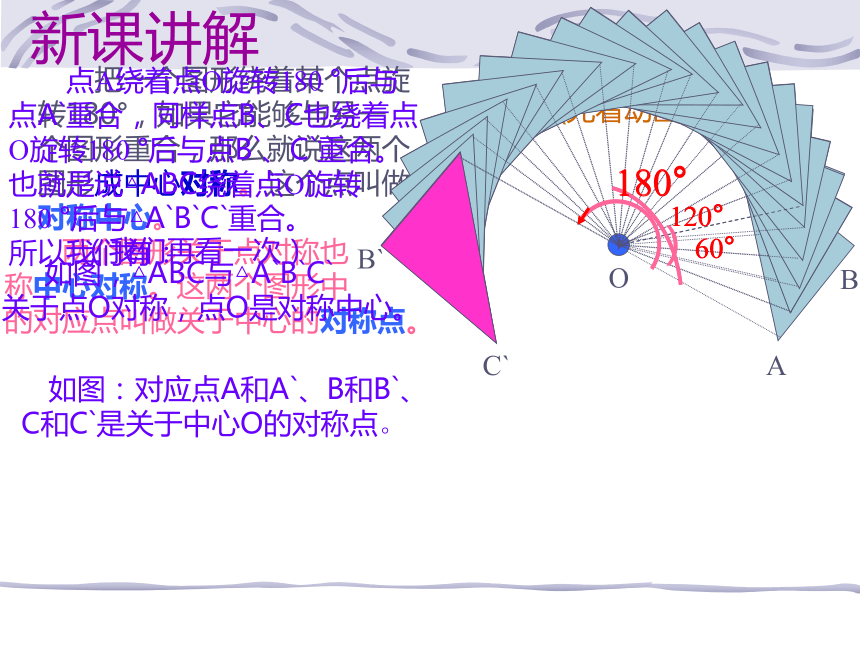
的对应点叫做关于中心的对称点。 如图：对应点A和A`、B和B`、C和C`是关于中心O的对称点。 如图，△ABC与△A`B`C`
关于点O对称，点O是对称中心。ABC新课讲解(先看动画) 把一个图形绕着某个点旋转180°，如果它能够与另一个图形重合，那么就说这两个图形成中心对称。这个点叫做对称中心。B`A`OC`（我们再看一次） 并且由图知OA
=OA′，同理有OB=OB′，OC=OC′。
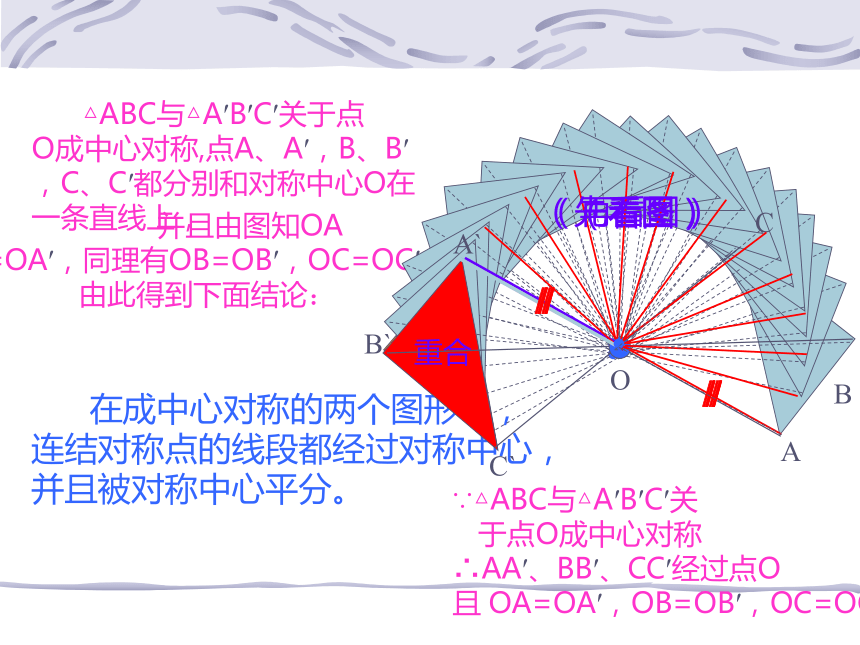
由此得到下面结论： 在成中心对称的两个图形中，连结对称点的线段都经过对称中心，并且被对称中心平分。 △ABC与△A′B′C′关于点
O成中心对称,点A、A′，B、B′
，C、C′都分别和对称中心O在
一条直线上，ABCC`B`A`O∵△ABC与△A′B′C′关
于点O成中心对称
∴AA′、BB′、CC′经过点O
且 OA=OA′，OB=OB′，OC=OC′（看图）（再看图）如果两个图形的对应点所连的线段都经过某一点，并且被这一点平分，那么这两个图形关于这一点成中心对称。（看图）结论是两个图形关于这点对称（看图）例题 已知四边形ABCD和点O（如图），画四边形
A′B′C′D′，使它与已知四边形关于点O对称。ABCDO分析：要画四边形ABCD关
于点O的对称图形，只要画
A、B、C、D四点关于点O
的对称点。再顺次连接各点
即可。画法：1。连接AO并延长到A′，使
OA=OA′，得到点A的对称点A′。2。同样画B、C、D的对称点B′、
C′、D′。3。顺次连接A′、B′、C′、D′各点。∴四边形A′B′C′D′就是所求的四边形。画一个与已知四边形ABCD中心对称图形。
（1）以顶点A为对称中心；
（2）以BC边的中点为对称中心。DABC∴四边形AEFG为（1）所求作。∴四边形BCMN为（2）所求作。提高练习怎样的两个图形叫做关于某直线成轴对称？成轴对称
的两个图形有什么性质？定义三要点性 质1 2 3有一条轴对称——直线图形沿轴对折，即翻转180°翻转后与另一图形重合1 2 3轴 对 称两个图形是全等形对称轴是对应点连线的垂直平分线对应线段或延长线相交，交点在
对称轴上中心对称有一个对称中心——点图形绕中心旋转180°旋转后与另一图形重合两个图形是全等形对称点连线都经过对称中心，并且被
对称中心平分。观察下列图形,你能发现它们有什么共同的特征吗?你能将上图中第一个图形绕其上的一点旋转180o，使旋转前后的图形完全重合吗？其余图形呢？定义 在平面内，一个图形绕某个点旋转 180o，如果旋转前后的图形互相重合，这个图形就叫做中心对称图形，这个点就叫做它的对称中心。生活中你见过哪些中心对称图形的具体实例？巩固练习1、仔细观察下列图案，然后回答下列问题：（填序号）
（1）是轴对称图形的有_______________.
　 （2）是旋转对称图形的有_______________.
　 （3）是中心对称图形的有_______________.
（4）既是轴对称又是中心对称图形的有_____________.
是是是是是是是是是否是是否否2.3.如图，四边形ABCD中，AD∥BC，DF=CF，
连结AF并延长交BC延长线于点E.
　 （1）图中哪两个三角形可以通过怎样的旋转而相互得到？
　 （2）四边形ABCD的面积与图中哪个三角形的面积相等？
　　（3）若AE=AD＋BC，∠B=70°，试求∠DAF的度数.
再见愿同学们学习进步!