数学人教A版(2019)选择性必修第一册3.3.1 抛物线及其标准方程 课件(共28张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册3.3.1 抛物线及其标准方程 课件(共28张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 7.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-06 14:42:39 | ||
图片预览





文档简介
(共28张PPT)
3.3.1 抛物线及其标准方程(一)
学习新知
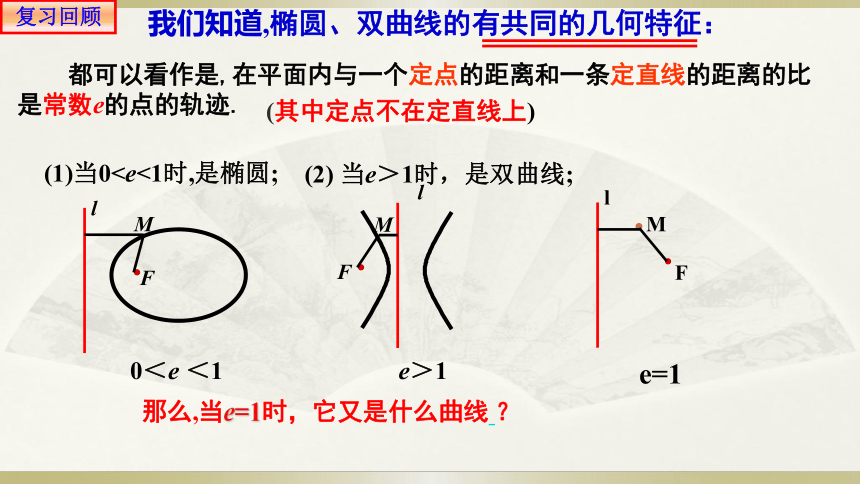
我们知道,椭圆、双曲线的有共同的几何特征:
都可以看作是,在平面内与一个定点的距离和一条定直线的距离的比是常数e的点的轨迹.
·
M
F
l
0<e <1
(2) 当e>1时,是双曲线;
(1)当0(其中定点不在定直线上)
l
F
·
M
e>1
那么,当e=1时,它又是什么曲线 ?
·
F
M
l
·
e=1
复习回顾
如图,点F是定点,l是不经过点F的定直线。 H是l上任意一点,过点H作MH⊥l,线段FH的垂直平分线m交MH于点M,拖动点H,观察点M的轨迹,你能发现点M满足的几何条件吗?
提出问题
M
F
探究?
可以发现,点M随着H运动的过程中,
始终有|MF|=|MH|,即点M与点F和
定直线l的距离相等.点M生成的轨迹
是曲线C的形状.(如图)
M
·
F
l
·
e=1
我们把这样的曲线叫做抛物线.
探究结果
M
·
F
l
·
e=1
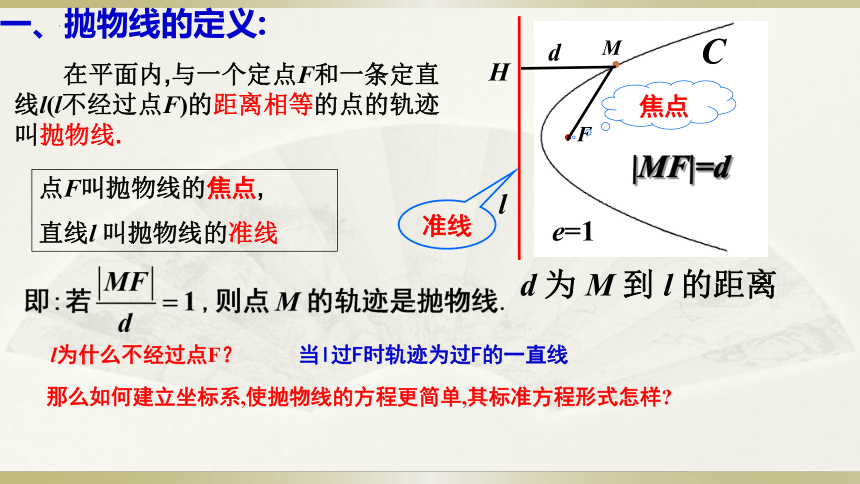
在平面内,与一个定点F和一条定直线l(l不经过点F)的距离相等的点的轨迹叫抛物线.
点F叫抛物线的焦点,
直线l 叫抛物线的准线
|MF|=d
d 为 M 到 l 的距离
准线
焦点
d
一、抛物线的定义:
那么如何建立坐标系,使抛物线的方程更简单,其标准方程形式怎样
l为什么不经过点F?
当l过F时轨迹为过F的一直线
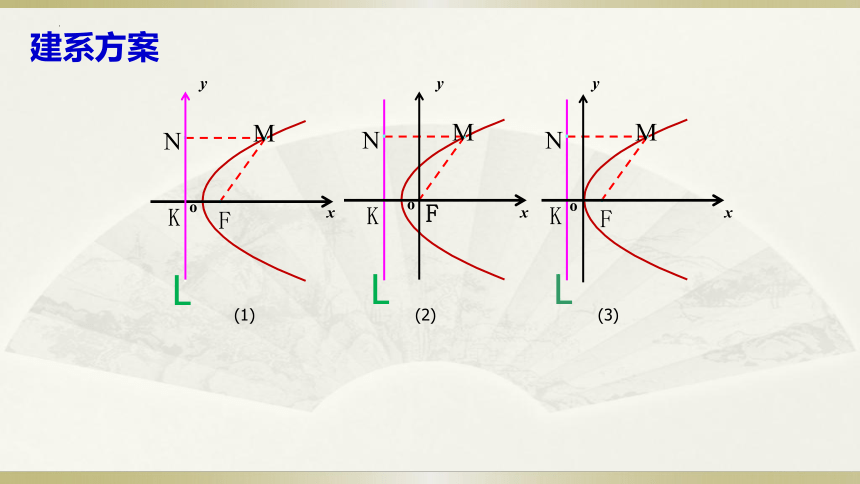
(1)
(2)
(3)
L
F
K
M
N
L
K
M
N
L
F
K
M
N
x
x
x
y
y
y
o
o
o
建系方案
F
建系 设点 找关系 化简并检验
回顾求曲线方程一般步骤:
复习回顾
方案一:以l为y轴,过F点垂直于l的直线为x轴建立直角坐标系(如下图所示),则定点 设动点 ,由抛物线定义得:
化简得:
.
M(x,y)
.
x
y
O
F
l
二、标准方程的推导
学习新知
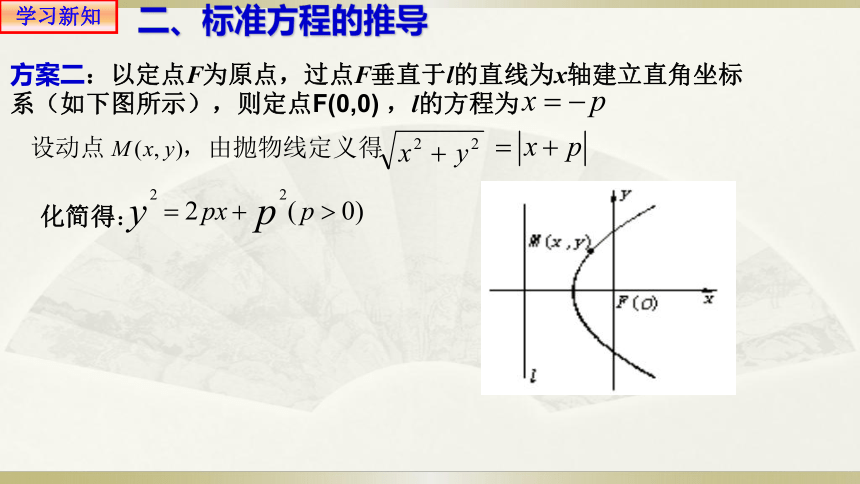
方案二:以定点F为原点,过点F垂直于l的直线为x轴建立直角坐标系(如下图所示),则定点F(0,0) ,l的方程为
设动点 ,由抛物线定义得
化简得:
二、标准方程的推导
学习新知
l
方案三:以过F且垂直于 l 的直线为x轴,垂足为K.以F,K的中点O为坐标原点建立直角坐标系xoy.
两边平方,整理得
x
K
y
o
M(x,y)
F
二、标准方程的推导
依题意得
这就是所求的轨迹方程.
学习新知
三、标准方程
把方程 y2 = 2px (p>0)叫做抛物线的标准方程.其中 p 为正常数,表示焦点在 x 轴正半轴上.
且 p的几何意义是:
焦点坐标是
准线方程为:
想一想: 坐标系的建立还有没有其它方案也会使抛物线方程的形式简单 ?
﹒
y
x
o
方案(1)
﹒
y
x
o
方案(2)
﹒
y
x
o
方案(3)
﹒
y
x
o
方案(4)
焦点到准线的距离
新知总结
相同点:
(1)顶点为原点;
(2)对称轴为坐标轴;
(3)顶点到焦点的距离等于顶点到准线的距离为p/2.
不同点:(1)一次项变量为x(y),则对称轴为x(y)轴;
(2)一次项系数为正(负),则开口方向坐标轴的正(负)方向.
记忆方法:P永为正,一次项变量为对称轴,一次项变量前系数为开口方向,且开口方向坐标轴的正(负)方向相同
新知总结
y2=-2px
(p>0)
x2=2py
(p>0)
准线方程
焦点坐标
标准方程
图 形
x
F
O
y
l
x
F
O
y
l
x
F
O
y
l
x
F
O
y
l
y2=2px
(p>0)
x2=-2py
(p>0)
P的意义:抛物线的焦点到准线的距离
方程的特点:
(1)左边是二次式,
(2)右边是一次式;决定了焦点的位置.
四.四种抛物线的对比
新知总结
二次函数 的图像为什么是抛物线?
当a>0时与当a<0时,结论都为:
P132思考:
y
x
o
y=ax2
y=ax2+c
y=ax2+bx+c
深入学习
例1(1)已知抛物线的标准方程是y2 =6x,求它的焦点坐标和准线方程;
(2)已知抛物线的焦点坐标是F(0,-2),求它的标准方程.
解:(1)因为p=3,所以焦点坐标是 , 准线方程是
,所以所求抛物线的标准方程是
(2)因为焦点在y轴的负半轴上,且
例题讲评
例1(3)已知抛物线的准线方程为 x = 1 ,求抛物线的标准方程
x
y
o
l
F
x = 1
解:因为准线方程是 x = 1,所以 p =2 ,且焦点在 x 轴的负半轴上,所以所求抛物线的标准方程是 y2 =-4x .
例题讲评
例1 (4)求过点A(3,2)的抛物线的标准方程
x
y
o
(3,2)
解:因为(3,2)点在第一象限,所以抛物线的开口方向只能是向右或向上,
故设抛物线的标准方程是 y2 = 2px(p>0),或 x2 = 2py(p>0),将(3,2)点的坐标分别代入上述方程可得抛物线的标准方程为
y 2 = x 或 x 2 = y
4
3
9
2
例题讲评
课堂练习
1、根据下列条件,写出抛物线的标准方程:
(1)焦点是F(3,0);
(2)准线方程 是x = ;
(3)焦点到准线的距离是2。
y2 =12x
y2 =x
y2 =4x,y2 = -4x,x2 =4y 或 x2 = -4y
2、求下列抛物线的焦点坐标和准线方程:
(1)y2 = 20x (2) x2= y
(3)2y2 +5x =0 (4) x2 +8y =0
焦点坐标 准线方程
(1)
(2)
(3)
(4)
(5,0)
x=-5
(0,—)
1
8
y= - —
1
8
8
x= —
5
(- —,0)
5
8
(0,-2)
y=2
课堂练习
课堂练习
例2:一种卫星接收天线的轴截面如下图所示。卫星波束呈近似平行状态射入轴截面为抛物线的接收天线,经反射聚集到焦点处。已知接收天线的径口(直径)为4.8m,深度为0.5m。建立适当的坐标系,求抛物线的标准方程和焦点坐标。
例题讲评
解:如上图,在接收天线的轴截面所在平面内建立直角坐标系,
使接收天线的顶点(即抛物线的顶点)与原点重合。
设抛物线的标准方程是 ,由已知条件
可得,点A的坐标是 ,代入方程,得
即
所以,所求抛物线的标准方程是 ,焦点的坐标是
例题讲评
3.四种不同类型抛物线图象的特征及判断方法
2.抛物线的标准方程与其焦点、准线
1.抛物线的定义
小结
临沂一中 李福国
抛物线 两端长 遥遥长臂向远方
似彩虹 如桥梁 世间英雄竟畅想
神舟飞 国兴旺 主宰世界非天王
看今朝 我辈忙 漫漫学路志昂扬
愿我们能乘着知识的翅膀,遨游苍穹------
划出一道美丽的抛物线!
过抛物线 的焦点 作一条直线 交抛物线于 , 两点,若线段 与 的长分别为 ,则 等于( )
A. B. C. D.
分析:抛物线 的标准方程为 ,其
焦点为 .
取特殊情况,即直线 平行与 轴,
则 ,如图。
故
课堂练习
例3、点M到点F(4,0)的距离比它到直线l:x+5=0的距离小1, 求点M的轨迹方程.
x
y
o
F(4,0)
M
x+5=0
例题讲评
l
F
A
A1
x
y
B
B1
例题讲评
例4、斜率为1的直线 经过抛物线 的焦点F,且与抛物线相交于A,B两点,求线段AB的长。
8
一、现实情境
学校举办了主题为“汲文化精粹,育时代新人”的文化节,进行现场直播时要求摄像设备能同时覆盖舞台和观众席。经过测算,只要使摄像机到舞台的中心和观众席的第一排距离相等即可。你知道摄像机应该按照怎样的路线运动吗?
F
汲
文
化
精
粹
育
时
代
新
人
∟
p
M
3.3.1 抛物线及其标准方程(一)
学习新知
我们知道,椭圆、双曲线的有共同的几何特征:
都可以看作是,在平面内与一个定点的距离和一条定直线的距离的比是常数e的点的轨迹.
·
M
F
l
0<e <1
(2) 当e>1时,是双曲线;
(1)当0
l
F
·
M
e>1
那么,当e=1时,它又是什么曲线 ?
·
F
M
l
·
e=1
复习回顾
如图,点F是定点,l是不经过点F的定直线。 H是l上任意一点,过点H作MH⊥l,线段FH的垂直平分线m交MH于点M,拖动点H,观察点M的轨迹,你能发现点M满足的几何条件吗?
提出问题
M
F
探究?
可以发现,点M随着H运动的过程中,
始终有|MF|=|MH|,即点M与点F和
定直线l的距离相等.点M生成的轨迹
是曲线C的形状.(如图)
M
·
F
l
·
e=1
我们把这样的曲线叫做抛物线.
探究结果
M
·
F
l
·
e=1
在平面内,与一个定点F和一条定直线l(l不经过点F)的距离相等的点的轨迹叫抛物线.
点F叫抛物线的焦点,
直线l 叫抛物线的准线
|MF|=d
d 为 M 到 l 的距离
准线
焦点
d
一、抛物线的定义:
那么如何建立坐标系,使抛物线的方程更简单,其标准方程形式怎样
l为什么不经过点F?
当l过F时轨迹为过F的一直线
(1)
(2)
(3)
L
F
K
M
N
L
K
M
N
L
F
K
M
N
x
x
x
y
y
y
o
o
o
建系方案
F
建系 设点 找关系 化简并检验
回顾求曲线方程一般步骤:
复习回顾
方案一:以l为y轴,过F点垂直于l的直线为x轴建立直角坐标系(如下图所示),则定点 设动点 ,由抛物线定义得:
化简得:
.
M(x,y)
.
x
y
O
F
l
二、标准方程的推导
学习新知
方案二:以定点F为原点,过点F垂直于l的直线为x轴建立直角坐标系(如下图所示),则定点F(0,0) ,l的方程为
设动点 ,由抛物线定义得
化简得:
二、标准方程的推导
学习新知
l
方案三:以过F且垂直于 l 的直线为x轴,垂足为K.以F,K的中点O为坐标原点建立直角坐标系xoy.
两边平方,整理得
x
K
y
o
M(x,y)
F
二、标准方程的推导
依题意得
这就是所求的轨迹方程.
学习新知
三、标准方程
把方程 y2 = 2px (p>0)叫做抛物线的标准方程.其中 p 为正常数,表示焦点在 x 轴正半轴上.
且 p的几何意义是:
焦点坐标是
准线方程为:
想一想: 坐标系的建立还有没有其它方案也会使抛物线方程的形式简单 ?
﹒
y
x
o
方案(1)
﹒
y
x
o
方案(2)
﹒
y
x
o
方案(3)
﹒
y
x
o
方案(4)
焦点到准线的距离
新知总结
相同点:
(1)顶点为原点;
(2)对称轴为坐标轴;
(3)顶点到焦点的距离等于顶点到准线的距离为p/2.
不同点:(1)一次项变量为x(y),则对称轴为x(y)轴;
(2)一次项系数为正(负),则开口方向坐标轴的正(负)方向.
记忆方法:P永为正,一次项变量为对称轴,一次项变量前系数为开口方向,且开口方向坐标轴的正(负)方向相同
新知总结
y2=-2px
(p>0)
x2=2py
(p>0)
准线方程
焦点坐标
标准方程
图 形
x
F
O
y
l
x
F
O
y
l
x
F
O
y
l
x
F
O
y
l
y2=2px
(p>0)
x2=-2py
(p>0)
P的意义:抛物线的焦点到准线的距离
方程的特点:
(1)左边是二次式,
(2)右边是一次式;决定了焦点的位置.
四.四种抛物线的对比
新知总结
二次函数 的图像为什么是抛物线?
当a>0时与当a<0时,结论都为:
P132思考:
y
x
o
y=ax2
y=ax2+c
y=ax2+bx+c
深入学习
例1(1)已知抛物线的标准方程是y2 =6x,求它的焦点坐标和准线方程;
(2)已知抛物线的焦点坐标是F(0,-2),求它的标准方程.
解:(1)因为p=3,所以焦点坐标是 , 准线方程是
,所以所求抛物线的标准方程是
(2)因为焦点在y轴的负半轴上,且
例题讲评
例1(3)已知抛物线的准线方程为 x = 1 ,求抛物线的标准方程
x
y
o
l
F
x = 1
解:因为准线方程是 x = 1,所以 p =2 ,且焦点在 x 轴的负半轴上,所以所求抛物线的标准方程是 y2 =-4x .
例题讲评
例1 (4)求过点A(3,2)的抛物线的标准方程
x
y
o
(3,2)
解:因为(3,2)点在第一象限,所以抛物线的开口方向只能是向右或向上,
故设抛物线的标准方程是 y2 = 2px(p>0),或 x2 = 2py(p>0),将(3,2)点的坐标分别代入上述方程可得抛物线的标准方程为
y 2 = x 或 x 2 = y
4
3
9
2
例题讲评
课堂练习
1、根据下列条件,写出抛物线的标准方程:
(1)焦点是F(3,0);
(2)准线方程 是x = ;
(3)焦点到准线的距离是2。
y2 =12x
y2 =x
y2 =4x,y2 = -4x,x2 =4y 或 x2 = -4y
2、求下列抛物线的焦点坐标和准线方程:
(1)y2 = 20x (2) x2= y
(3)2y2 +5x =0 (4) x2 +8y =0
焦点坐标 准线方程
(1)
(2)
(3)
(4)
(5,0)
x=-5
(0,—)
1
8
y= - —
1
8
8
x= —
5
(- —,0)
5
8
(0,-2)
y=2
课堂练习
课堂练习
例2:一种卫星接收天线的轴截面如下图所示。卫星波束呈近似平行状态射入轴截面为抛物线的接收天线,经反射聚集到焦点处。已知接收天线的径口(直径)为4.8m,深度为0.5m。建立适当的坐标系,求抛物线的标准方程和焦点坐标。
例题讲评
解:如上图,在接收天线的轴截面所在平面内建立直角坐标系,
使接收天线的顶点(即抛物线的顶点)与原点重合。
设抛物线的标准方程是 ,由已知条件
可得,点A的坐标是 ,代入方程,得
即
所以,所求抛物线的标准方程是 ,焦点的坐标是
例题讲评
3.四种不同类型抛物线图象的特征及判断方法
2.抛物线的标准方程与其焦点、准线
1.抛物线的定义
小结
临沂一中 李福国
抛物线 两端长 遥遥长臂向远方
似彩虹 如桥梁 世间英雄竟畅想
神舟飞 国兴旺 主宰世界非天王
看今朝 我辈忙 漫漫学路志昂扬
愿我们能乘着知识的翅膀,遨游苍穹------
划出一道美丽的抛物线!
过抛物线 的焦点 作一条直线 交抛物线于 , 两点,若线段 与 的长分别为 ,则 等于( )
A. B. C. D.
分析:抛物线 的标准方程为 ,其
焦点为 .
取特殊情况,即直线 平行与 轴,
则 ,如图。
故
课堂练习
例3、点M到点F(4,0)的距离比它到直线l:x+5=0的距离小1, 求点M的轨迹方程.
x
y
o
F(4,0)
M
x+5=0
例题讲评
l
F
A
A1
x
y
B
B1
例题讲评
例4、斜率为1的直线 经过抛物线 的焦点F,且与抛物线相交于A,B两点,求线段AB的长。
8
一、现实情境
学校举办了主题为“汲文化精粹,育时代新人”的文化节,进行现场直播时要求摄像设备能同时覆盖舞台和观众席。经过测算,只要使摄像机到舞台的中心和观众席的第一排距离相等即可。你知道摄像机应该按照怎样的路线运动吗?
F
汲
文
化
精
粹
育
时
代
新
人
∟
p
M
