24.3正多边形和圆(1)课件[上学期]
文档属性
| 名称 | 24.3正多边形和圆(1)课件[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 378.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-10-02 16:48:00 | ||
图片预览

文档简介
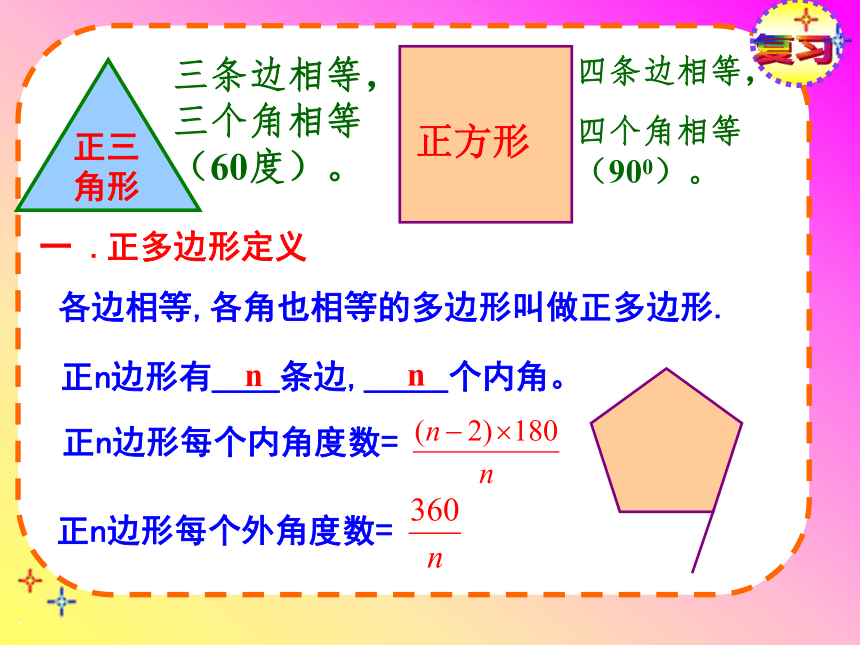
课件20张PPT。24.3正多边形和圆(1)复习观察下列图形他们有什么特点?复习三条边相等,三个角相等(60度)。四条边相等,
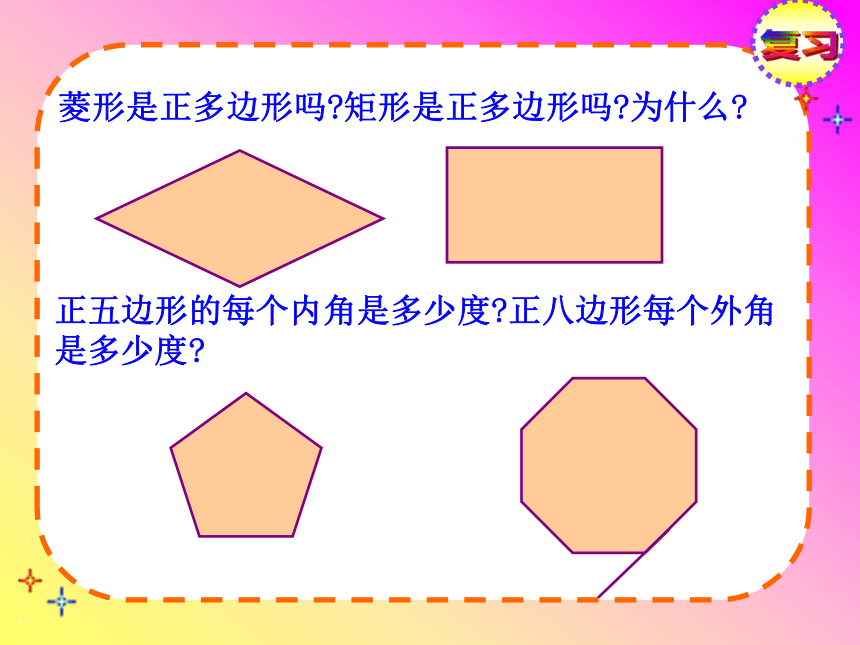
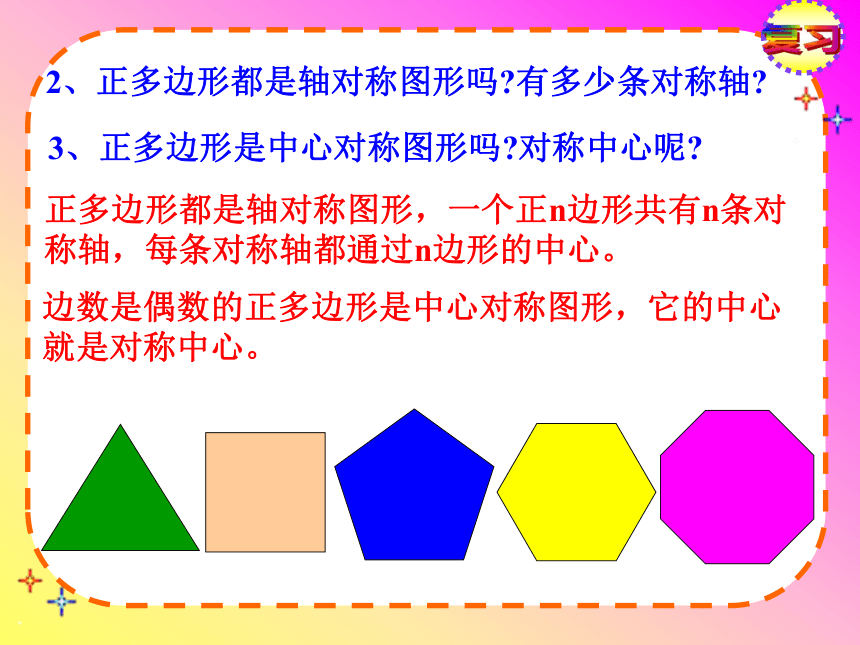
四个角相等(900)。一 .正多边形定义各边相等,各角也相等的多边形叫做正多边形.正n边形有____条边,_____个内角。正n边形每个内角度数=正n边形每个外角度数=nn复习菱形是正多边形吗?矩形是正多边形吗?为什么?正五边形的每个内角是多少度?正八边形每个外角是多少度?复习2、正多边形都是轴对称图形吗?有多少条对称轴?正多边形都是轴对称图形,一个正n边形共有n条对称轴,每条对称轴都通过n边形的中心。3、正多边形是中心对称图形吗?对称中心呢?边数是偶数的正多边形是中心对称图形,它的中心就是对称中心。运用正n边形与圆有密切的关系 1.把正n边形的边数无限增多,就接近于圆.
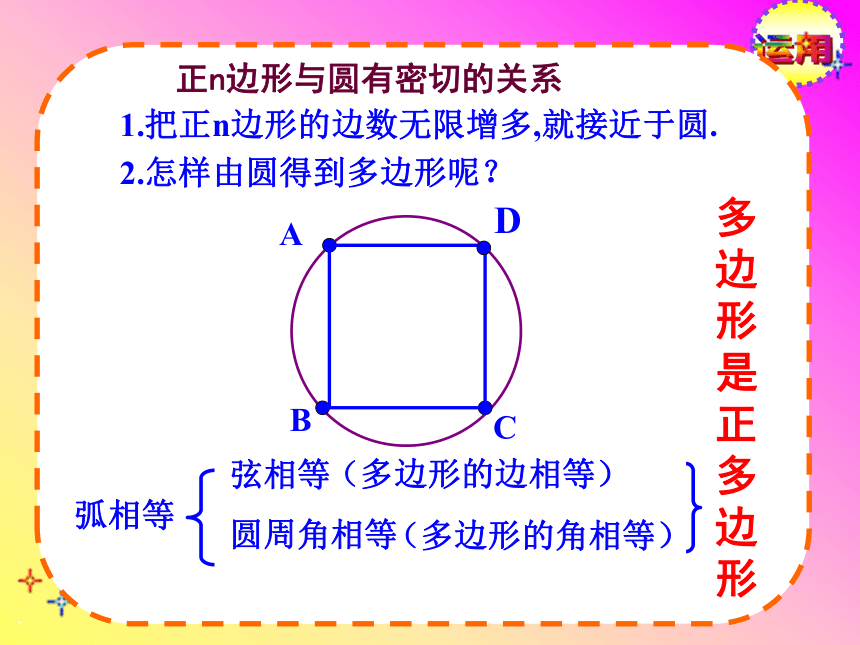
2.怎样由圆得到多边形呢? 弦相等
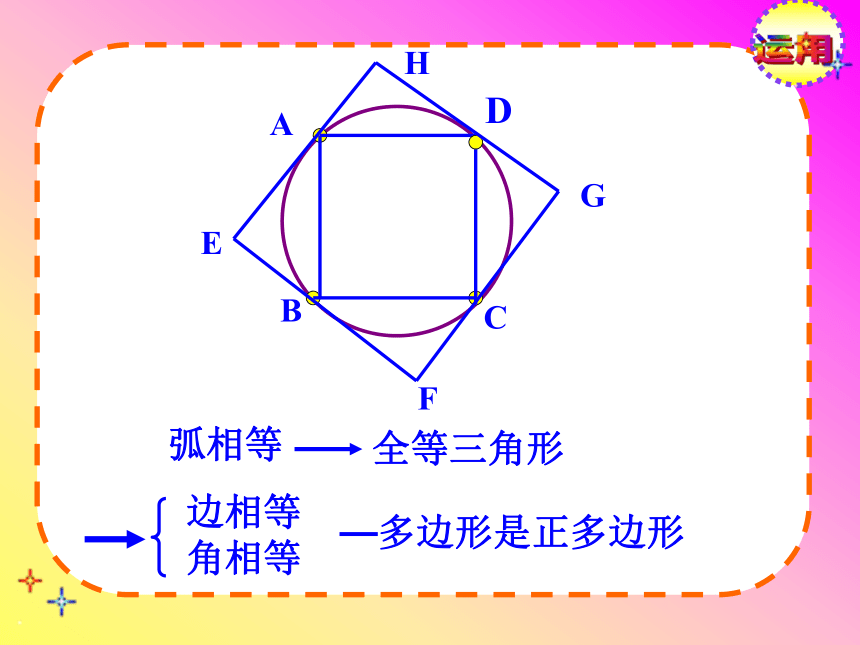
圆周角相等多边形是正多边形ABCD弧相等(多边形的边相等)(多边形的角相等)运用EFGH 边相等
角相等弧相等全等三角形—多边形是正多边形运用定理:
把圆分成n(n≥3)等份:
⑴依次连结各分点所得的多边形是这个圆的
内接正多边形;
⑵经过各分点作圆的切线,以相邻切线的交
点为顶点的多边形是这个圆的外切正多边
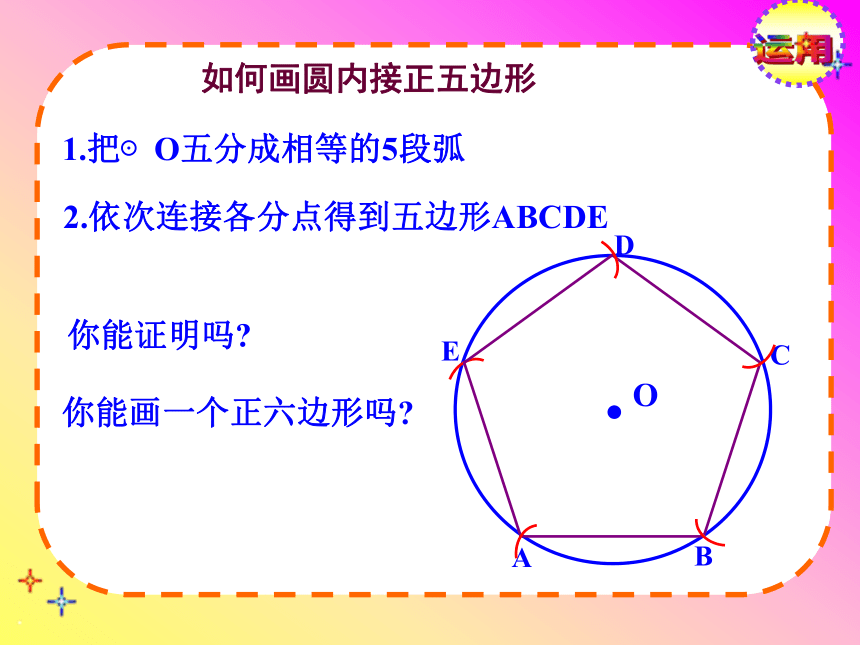
形。正多边形的中心也是内切圆和外接圆的圆心运用如何画圆内接正五边形ECDAB1.把⊙O五分成相等的5段弧2.依次连接各分点得到五边形ABCDE你能证明吗?你能画一个正六边形吗?O运用EFCD.O中心角半径R边心距r正多边形的中心:一个正多边形的外接圆的圆心.正多边形的半径:外接圆的半径正多边形的中心角:
正多边形的每一条
边所对的圆心角.正多边形的边心距:
中心到正多边形的一边
的距离.二. 正多边形有关的概念AB正n边形的中心角=运用1、O是正
与_________圆的圆心。△ABC的中心,它是△ABC的_______2、OB叫正△ABC的_______,它是正△ABC的
_________圆的半径。 3、OD叫作正△ABC的________,它是正△ABC的_______圆的半径。ABC .OD外接圆内切圆边心距外接圆内切圆半径4、正△ABC的中心角为________度,120运用5、图中正六边形ABCDEF的中心角是________
它的度数是_________6、你发现正六边形ABCDEF的半径与边长具有
什么数量关系?为什么? BA∠AOB60度正n边形被边心距分成
____个全等的直角三角形,
被相邻半径分成______个
全等的等腰三角形.结论:边心距把△AOB分成
2个全等的直角三角形边心距r2nn运用ABCDE求证:正五边形的对角线相等。证明: 在△BCD和△CDE中
∵BC=CD
∠BCD=∠CDE
CD=DE
∴△BCD≌△CDE
∴BD=CE
同理可证其他对角线相等。已知:ABCDE是正五边形,求证:DB=CE运用例.有一个亭子它的地基是半径为4m的正六边形,求地基的周长和面积(精确到0.1㎡)..OBCrRP亭子的周长 L=6×4=24(m)练习正三角形的边长为a,则它的外接圆O的面积是多少? O⊙O的外切等边三角形的边长是多少?运用1、两个正六边形的边长分别是3和4,这两个正六边形的面积之比等于________
2.圆内接正方形的半径与边长的比值是________
3.圆内接正四边形的边长为4 cm,那么边心距是________
4.已知圆内接正方形的边长为,则该圆 的内接正六边形边长为__________.
5. 圆内接正六边形的边长是8 cm用么该正六边形的半径为________;边心距为________. 回顾6、已知正多边形的边心距与边长的比是,则此正多边形是( )
A.正三角形 B.正方形 C.正六边形 D.正十二边形
7.以下有四种说法:①顺次连结对角线相等的四边形各边中点,则所得的四边形是菱形;②等边三角形是轴对称图形,但不是中心对称图形;③顶点在圆周上的角是圆周角;④边数相同的正多边形都相似,其中正确的有()
A.1个 B.2个 C.3个 D 4
8.正多边形的中心角与该正多边形一个内角的关系是()
A.互余 B.互补 C.互余或互补 D.不能确定回顾9.若一个正多边形的每一个外角都等于36°,那么这个正多边形的中心角为( )
A.36° B、 18° C.72° D.54°
10.将一个边长为a正方形硬纸片剪去四角,使它成为正n边形,那么正n边形的面积为( )
11.正六边形螺帽的边长为a,那么扳手的开口b最小应是( )
练习O定理: 概念:计算:正多边形正多边形中心正多边形半径正多边形的边心距正多边形的中心角半径、边心距、中心角的计算边长、面积的计算画法:量角器等分圆周画正多边形计算:把多边形问题转化成三角形问题来解决 再见
四个角相等(900)。一 .正多边形定义各边相等,各角也相等的多边形叫做正多边形.正n边形有____条边,_____个内角。正n边形每个内角度数=正n边形每个外角度数=nn复习菱形是正多边形吗?矩形是正多边形吗?为什么?正五边形的每个内角是多少度?正八边形每个外角是多少度?复习2、正多边形都是轴对称图形吗?有多少条对称轴?正多边形都是轴对称图形,一个正n边形共有n条对称轴,每条对称轴都通过n边形的中心。3、正多边形是中心对称图形吗?对称中心呢?边数是偶数的正多边形是中心对称图形,它的中心就是对称中心。运用正n边形与圆有密切的关系 1.把正n边形的边数无限增多,就接近于圆.
2.怎样由圆得到多边形呢? 弦相等
圆周角相等多边形是正多边形ABCD弧相等(多边形的边相等)(多边形的角相等)运用EFGH 边相等
角相等弧相等全等三角形—多边形是正多边形运用定理:
把圆分成n(n≥3)等份:
⑴依次连结各分点所得的多边形是这个圆的
内接正多边形;
⑵经过各分点作圆的切线,以相邻切线的交
点为顶点的多边形是这个圆的外切正多边
形。正多边形的中心也是内切圆和外接圆的圆心运用如何画圆内接正五边形ECDAB1.把⊙O五分成相等的5段弧2.依次连接各分点得到五边形ABCDE你能证明吗?你能画一个正六边形吗?O运用EFCD.O中心角半径R边心距r正多边形的中心:一个正多边形的外接圆的圆心.正多边形的半径:外接圆的半径正多边形的中心角:
正多边形的每一条
边所对的圆心角.正多边形的边心距:
中心到正多边形的一边
的距离.二. 正多边形有关的概念AB正n边形的中心角=运用1、O是正
与_________圆的圆心。△ABC的中心,它是△ABC的_______2、OB叫正△ABC的_______,它是正△ABC的
_________圆的半径。 3、OD叫作正△ABC的________,它是正△ABC的_______圆的半径。ABC .OD外接圆内切圆边心距外接圆内切圆半径4、正△ABC的中心角为________度,120运用5、图中正六边形ABCDEF的中心角是________
它的度数是_________6、你发现正六边形ABCDEF的半径与边长具有
什么数量关系?为什么? BA∠AOB60度正n边形被边心距分成
____个全等的直角三角形,
被相邻半径分成______个
全等的等腰三角形.结论:边心距把△AOB分成
2个全等的直角三角形边心距r2nn运用ABCDE求证:正五边形的对角线相等。证明: 在△BCD和△CDE中
∵BC=CD
∠BCD=∠CDE
CD=DE
∴△BCD≌△CDE
∴BD=CE
同理可证其他对角线相等。已知:ABCDE是正五边形,求证:DB=CE运用例.有一个亭子它的地基是半径为4m的正六边形,求地基的周长和面积(精确到0.1㎡)..OBCrRP亭子的周长 L=6×4=24(m)练习正三角形的边长为a,则它的外接圆O的面积是多少? O⊙O的外切等边三角形的边长是多少?运用1、两个正六边形的边长分别是3和4,这两个正六边形的面积之比等于________
2.圆内接正方形的半径与边长的比值是________
3.圆内接正四边形的边长为4 cm,那么边心距是________
4.已知圆内接正方形的边长为,则该圆 的内接正六边形边长为__________.
5. 圆内接正六边形的边长是8 cm用么该正六边形的半径为________;边心距为________. 回顾6、已知正多边形的边心距与边长的比是,则此正多边形是( )
A.正三角形 B.正方形 C.正六边形 D.正十二边形
7.以下有四种说法:①顺次连结对角线相等的四边形各边中点,则所得的四边形是菱形;②等边三角形是轴对称图形,但不是中心对称图形;③顶点在圆周上的角是圆周角;④边数相同的正多边形都相似,其中正确的有()
A.1个 B.2个 C.3个 D 4
8.正多边形的中心角与该正多边形一个内角的关系是()
A.互余 B.互补 C.互余或互补 D.不能确定回顾9.若一个正多边形的每一个外角都等于36°,那么这个正多边形的中心角为( )
A.36° B、 18° C.72° D.54°
10.将一个边长为a正方形硬纸片剪去四角,使它成为正n边形,那么正n边形的面积为( )
11.正六边形螺帽的边长为a,那么扳手的开口b最小应是( )
练习O定理: 概念:计算:正多边形正多边形中心正多边形半径正多边形的边心距正多边形的中心角半径、边心距、中心角的计算边长、面积的计算画法:量角器等分圆周画正多边形计算:把多边形问题转化成三角形问题来解决 再见
同课章节目录
