正多边形的有关计算[上学期]
文档属性
| 名称 | 正多边形的有关计算[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 39.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-12-14 13:49:00 | ||
图片预览

文档简介
正多边形的有关计算
教学 ( http: / / www.pjnj.com" \t "_blank )设计示例1
教学 ( http: / / www.pjnj.com" \t "_blank )目标:
(1)会将正多边形的边长、半径、边心距和中心角、周长、面积等有关的计算问题转化为解直角三角形的问题;
(2)巩固学生解直角三角形的能力,培养学生正确迅速的运算能力;
(3)通过正多边形有关计算公式的推导,激发学生探索和创新.
教学 ( http: / / www.pjnj.com" \t "_blank )重点:
把正多边形的有关计算问题转化为解直角三角形的问题.
教学 ( http: / / www.pjnj.com" \t "_blank )难点:
正确地将正多边形的有关计算问题转化为解直角三角形的问题解决、综合运用几何知识准确计算.
教学 ( http: / / www.pjnj.com" \t "_blank )活动设计:
(一)创设情境、观察、分析、归纳结论
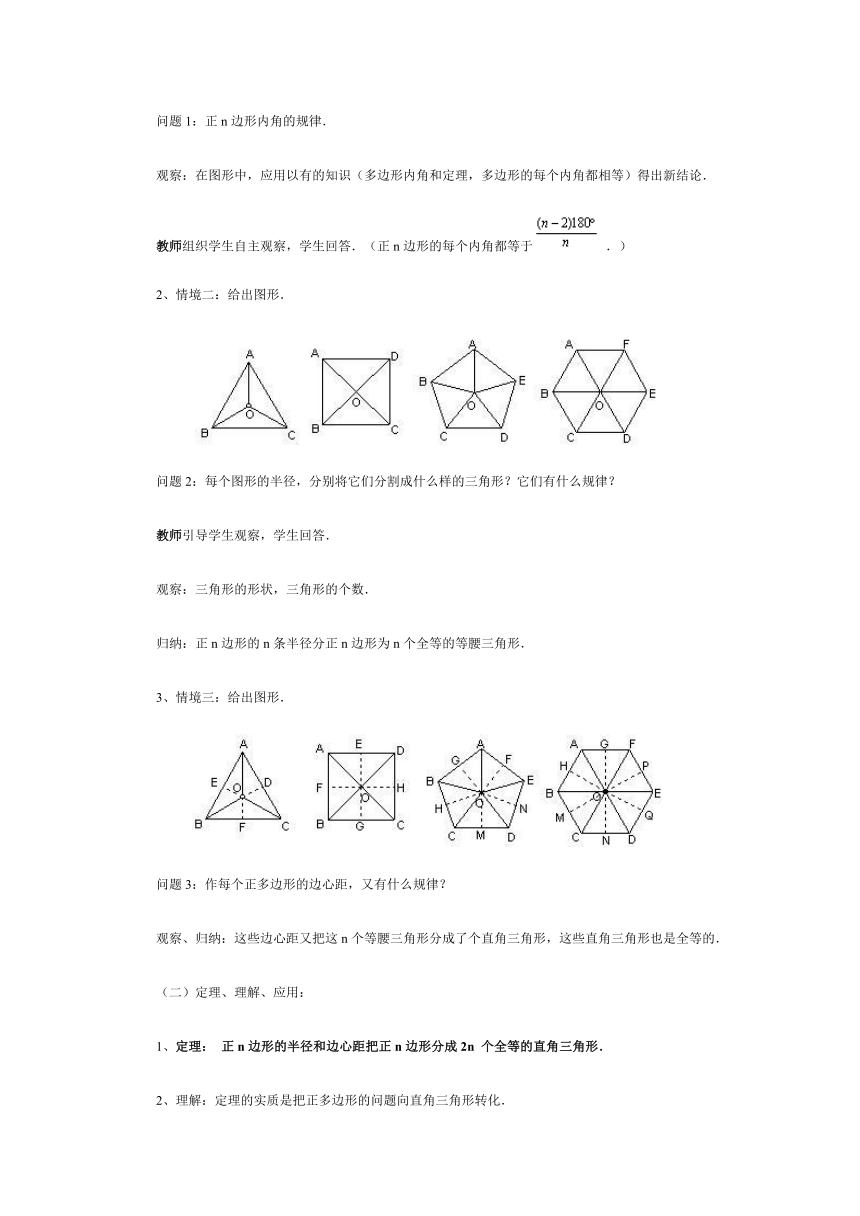
1、情境一:给出图形.
问题1:正n边形内角的规律.
观察:在图形中,应用以有的知识(多边形内角和定理,多边形的每个内角都相等)得出新结论.
教师 ( http: / / www.pjnj.com" \t "_blank )组织学生自主观察,学生回答.(正n边形的每个内角都等于 .)
2、情境二:给出图形.
问题2:每个图形的半径,分别将它们分割成什么样的三角形?它们有什么规律?
教师 ( http: / / www.pjnj.com" \t "_blank )引导学生观察,学生回答.
观察:三角形的形状,三角形的个数.
归纳:正n边形的n条半径分正n边形为n个全等的等腰三角形.
3、情境三:给出图形.
问题3:作每个正多边形的边心距,又有什么规律?
观察、归纳:这些边心距又把这n个等腰三角形分成了个直角三角形,这些直角三角形也是全等的.
(二)定理、理解、应用:
1、定理: 正n边形的半径和边心距把正n边形分成2n 个全等的直角三角形.
2、理解:定理的实质是把正多边形的问题向直角三角形转化.
由于这些直角三角形的斜边都是正n边形的半径R,一条直角边是正n边形的边心距rn,另一条直角边是正n边形边长an的一半,一个锐角是正n边形中心角 的一半,即 ,所以,根据上面定理就可以把正n边形的有关计算归结为解直角三角形问题.
3、应用:
例1、已知正六边形ABCDEF的半径为R,求这个正六边形的边长、周长P6和面积S6.
教师 ( http: / / www.pjnj.com" \t "_blank )引导学生分析解题思路:
n=6 =30°,又半径为R a6 、r6. P6、S6.
学生完成解题过程,并关注学生解直角三角形的能力.
解:作半径OA、OB;作OG⊥AB,垂足为G,得Rt△OGB.
∵∠GOB= ,
∴a6 =2·Rsin30°=R,
∴P6=6·a6=6R,
∵r6=Rcos30°= ,
∴ .
归纳:如果用Pn表示正n边形的周长,由例1可知,正n边形的面积S6= Pn rn.
4、研究:(应用例1的方法进一步研究)
问题:已知圆的半径为R,求它的内接正三角形、正方形的边长、边心距及面积.
学生以小组进行研究,并初步归纳:
; ; ; ;
; .
上述公式是运用解直角三角形的方法得到的.
通过上式六公式看出,只要给定两个条件,则正多边形就完全确定了.例如:(1)圆的半径或边数;(2)圆的半径和边心距;(3)边长及边心距,就可以确定正多边形的其它元素.
(三)小节
知识:定理、正三角形、正方形、正六边形的元素的计算问题.
思想:转化思想.
能力:解直角三角形的能力、计算能力;观察、分析、研究、归纳能力.
(四)作业
归纳正三角形、正方形、正六边形以及正n边形的有关计算公式.
教学 ( http: / / www.pjnj.com" \t "_blank )设计示例1
教学 ( http: / / www.pjnj.com" \t "_blank )目标:
(1)会将正多边形的边长、半径、边心距和中心角、周长、面积等有关的计算问题转化为解直角三角形的问题;
(2)巩固学生解直角三角形的能力,培养学生正确迅速的运算能力;
(3)通过正多边形有关计算公式的推导,激发学生探索和创新.
教学 ( http: / / www.pjnj.com" \t "_blank )重点:
把正多边形的有关计算问题转化为解直角三角形的问题.
教学 ( http: / / www.pjnj.com" \t "_blank )难点:
正确地将正多边形的有关计算问题转化为解直角三角形的问题解决、综合运用几何知识准确计算.
教学 ( http: / / www.pjnj.com" \t "_blank )活动设计:
(一)创设情境、观察、分析、归纳结论
1、情境一:给出图形.
问题1:正n边形内角的规律.
观察:在图形中,应用以有的知识(多边形内角和定理,多边形的每个内角都相等)得出新结论.
教师 ( http: / / www.pjnj.com" \t "_blank )组织学生自主观察,学生回答.(正n边形的每个内角都等于 .)
2、情境二:给出图形.
问题2:每个图形的半径,分别将它们分割成什么样的三角形?它们有什么规律?
教师 ( http: / / www.pjnj.com" \t "_blank )引导学生观察,学生回答.
观察:三角形的形状,三角形的个数.
归纳:正n边形的n条半径分正n边形为n个全等的等腰三角形.
3、情境三:给出图形.
问题3:作每个正多边形的边心距,又有什么规律?
观察、归纳:这些边心距又把这n个等腰三角形分成了个直角三角形,这些直角三角形也是全等的.
(二)定理、理解、应用:
1、定理: 正n边形的半径和边心距把正n边形分成2n 个全等的直角三角形.
2、理解:定理的实质是把正多边形的问题向直角三角形转化.
由于这些直角三角形的斜边都是正n边形的半径R,一条直角边是正n边形的边心距rn,另一条直角边是正n边形边长an的一半,一个锐角是正n边形中心角 的一半,即 ,所以,根据上面定理就可以把正n边形的有关计算归结为解直角三角形问题.
3、应用:
例1、已知正六边形ABCDEF的半径为R,求这个正六边形的边长、周长P6和面积S6.
教师 ( http: / / www.pjnj.com" \t "_blank )引导学生分析解题思路:
n=6 =30°,又半径为R a6 、r6. P6、S6.
学生完成解题过程,并关注学生解直角三角形的能力.
解:作半径OA、OB;作OG⊥AB,垂足为G,得Rt△OGB.
∵∠GOB= ,
∴a6 =2·Rsin30°=R,
∴P6=6·a6=6R,
∵r6=Rcos30°= ,
∴ .
归纳:如果用Pn表示正n边形的周长,由例1可知,正n边形的面积S6= Pn rn.
4、研究:(应用例1的方法进一步研究)
问题:已知圆的半径为R,求它的内接正三角形、正方形的边长、边心距及面积.
学生以小组进行研究,并初步归纳:
; ; ; ;
; .
上述公式是运用解直角三角形的方法得到的.
通过上式六公式看出,只要给定两个条件,则正多边形就完全确定了.例如:(1)圆的半径或边数;(2)圆的半径和边心距;(3)边长及边心距,就可以确定正多边形的其它元素.
(三)小节
知识:定理、正三角形、正方形、正六边形的元素的计算问题.
思想:转化思想.
能力:解直角三角形的能力、计算能力;观察、分析、研究、归纳能力.
(四)作业
归纳正三角形、正方形、正六边形以及正n边形的有关计算公式.
同课章节目录
