11.1.1三角形的边 课件(共24张PPT)
文档属性
| 名称 | 11.1.1三角形的边 课件(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 783.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-06 21:59:00 | ||
图片预览





文档简介
(共24张PPT)
11.1.1 三角形的边
学习目标
1、理解三角形的相关概念、表示方法和分类;
2、掌握三角形三边的关系,并能初步应用;
3、进一步体验分类讨论思想的应用。
1、什么是三角形、边、顶点、角?怎么表示三角形?
2、三角形按角、边各怎样分类?
自学指导
阅读课本P1-4,思考以下问题:
3、三角形三边有怎样的关系?为什么?
4、例题蕴含了怎样的数学思想方法?
5、完成课本P4【练习】
时间:7分钟
2.26米
姚明有多高?有人说姚明可以一步走四米!!可能吗?为什么?
由不在同一条直线上的三条线段首尾顺次相接所组成的图形,叫做三角形。
三角形的定义
三角形有关概念
三角形的顶点:___、___、____
三角形的内角:___、___、____
三角形的边:_____、____、_____
A
B
C
点A
点B
点C
∠A
∠B
∠C
线段BC
线段AB
线段CA
注意:三角形ABC的三边,有时也用a,b,c来表示.
b
a
c
A
B
C
三角形用符号“△”表示
记作“△ABC”读作“三角形ABC”
除此△ABC还可记作△BCA, △CAB,△ACB等
三角形有关概念
A
D
C
B
E
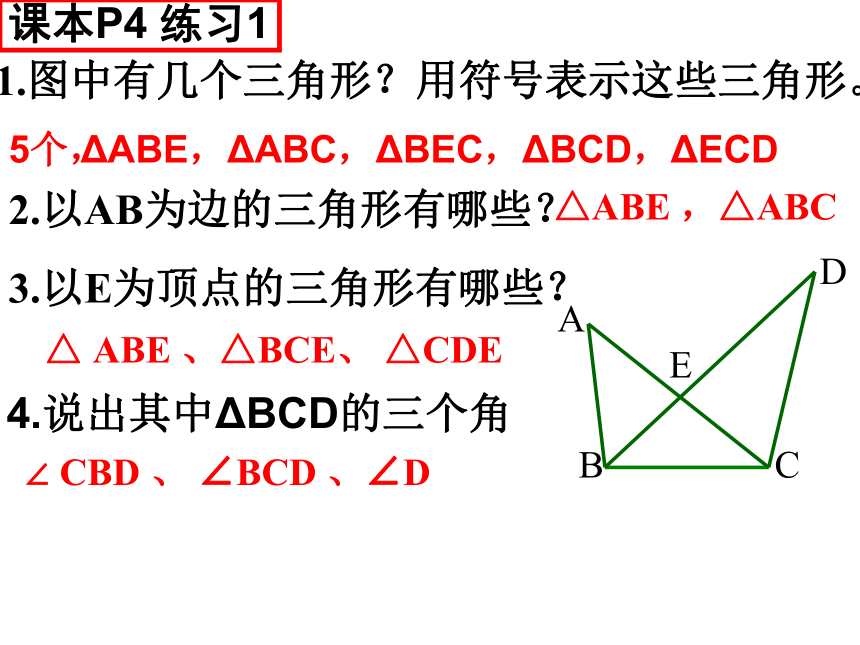
1.图中有几个三角形?用符号表示这些三角形。
2.以AB为边的三角形有哪些?
△ABE ,△ABC
3.以E为顶点的三角形有哪些?
△ ABE 、△BCE、 △CDE
ΔABE,ΔABC,ΔBEC,ΔBCD,ΔECD
4.说出其中ΔBCD的三个角
∠ CBD 、 ∠BCD 、∠D
课本P4 练习1
5个,
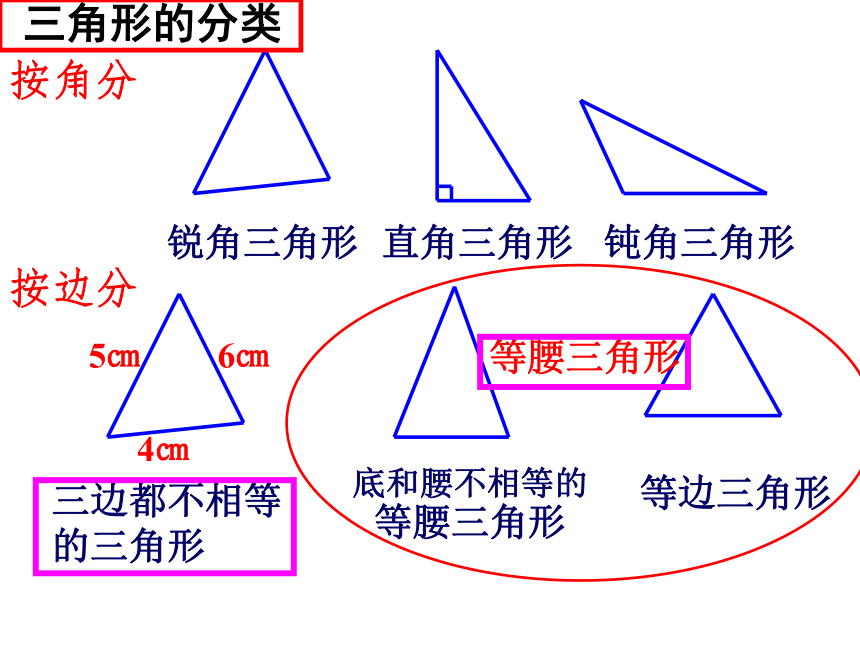
按角分
按边分
锐角三角形
直角三角形
钝角三角形
三边都不相等 的三角形
等腰三角形
等边三角形
底和腰不相等的
6㎝
4㎝
5㎝
三角形的分类
等腰三角形
注意:等腰三角形相等的两条边都叫做腰,另一边叫做
底边;两腰的夹角叫顶角,腰和底边的夹角叫底角。
A
B
C
腰
腰
底边
顶角
底角
底角
三角形三边之间的关系
它选择B—A路线,而不选择B—C—A路线,小狗的依据是什么?
C
B
A
两点之间,线段最短!
BC+AC>AB
同理可得:AC+AB>BC,AB+BC>AC
三角形任意两边之和大于第三边。
c
b
a
A
B
C
三角形三边之间的关系
如:a+b>c
a>c-b
c-b三角形任意两边之差小于第三边。
三角形任意两边之和大于第三边。
有人说姚明一步能走4米
不可能
你相信吗?
课本P4【练习】 第2题
下列长度的三条线段能否组成三角形?
(1)3、4、8;(2)5、6、11;
(3)5、6、10
5. 已知a,b,c是三角形的三条边长,试化简:
6、长为10、7、5、3的四根木条,选其
中的三根组成三角形,有____种选法。
练:放风筝是中华民族的传统娱乐项目,小林为了做一个三角形风筝架,找到长度分别为3m和5m的两根木棍,那么他要寻找的第三根木棍a的长度的范围应是___________.
2m例用一条长18cm的细绳围成一个等腰三角形。
(1)如果腰长是底长的2倍,那么各边的边长
是多少?
(2)能围成有一边的长是4 cm的等腰三角形吗?为什么?
例题讲解
1、如果等腰三角形的两边分别为4和6,
求它的周长。
变式:如果等腰三角形的两边分别为3和7,
求它的周长。
2、三角形三边的比为2:3:4,周长为36cm,
求三角形的边长。
综合练习(注意格式)
图中有几个三角形?
把它们一一写出来.
D
A
B
C
E
F
G
当堂训练
2、下列给出的三条线段不能组成三角形的是( )
A. 5cm,4cm,3cm
B.三条线段之比为2:3:5
C. 5m, 2m,6m
D.a=m+1,b=m+2,c=m+3(m>0)
B
3、若三角形的三边a、b、c 满足
|a-6|+(11-c)2+|6-b|=0,则△ABC是( )
A.不等边三角形 B.等腰三角形
C.等边三角形 D.以上答案都不对
B
当堂训练
4、长为10、7、5、3的四根木条,选其中的三根
组成三角形,有____种选法。
2
5、一个三角形两边长分别为3和7,
(1)第三边的长c的取值范围是___________;
(2)若第三边长为偶数,第三边长是_____________;
(3)三角形的周长p的取值范围是___________;
46或8
14当堂训练
《基础小练习》P1-2
当堂检测
草原上的四口油井,位于如图所示的A、B、
C、D四个位置,现在要建立一个维修站H,
问H建在何处,才能使它到四个油井的距离之和HA+HB+HC+HD为最小?说明理由。
A
D
C
B
H
H′
拓展与应用
1、《全品》课时一
2、预习课本P4-5,完成P5练习(完成在课本上)
作业
11.1.1 三角形的边
学习目标
1、理解三角形的相关概念、表示方法和分类;
2、掌握三角形三边的关系,并能初步应用;
3、进一步体验分类讨论思想的应用。
1、什么是三角形、边、顶点、角?怎么表示三角形?
2、三角形按角、边各怎样分类?
自学指导
阅读课本P1-4,思考以下问题:
3、三角形三边有怎样的关系?为什么?
4、例题蕴含了怎样的数学思想方法?
5、完成课本P4【练习】
时间:7分钟
2.26米
姚明有多高?有人说姚明可以一步走四米!!可能吗?为什么?
由不在同一条直线上的三条线段首尾顺次相接所组成的图形,叫做三角形。
三角形的定义
三角形有关概念
三角形的顶点:___、___、____
三角形的内角:___、___、____
三角形的边:_____、____、_____
A
B
C
点A
点B
点C
∠A
∠B
∠C
线段BC
线段AB
线段CA
注意:三角形ABC的三边,有时也用a,b,c来表示.
b
a
c
A
B
C
三角形用符号“△”表示
记作“△ABC”读作“三角形ABC”
除此△ABC还可记作△BCA, △CAB,△ACB等
三角形有关概念
A
D
C
B
E
1.图中有几个三角形?用符号表示这些三角形。
2.以AB为边的三角形有哪些?
△ABE ,△ABC
3.以E为顶点的三角形有哪些?
△ ABE 、△BCE、 △CDE
ΔABE,ΔABC,ΔBEC,ΔBCD,ΔECD
4.说出其中ΔBCD的三个角
∠ CBD 、 ∠BCD 、∠D
课本P4 练习1
5个,
按角分
按边分
锐角三角形
直角三角形
钝角三角形
三边都不相等 的三角形
等腰三角形
等边三角形
底和腰不相等的
6㎝
4㎝
5㎝
三角形的分类
等腰三角形
注意:等腰三角形相等的两条边都叫做腰,另一边叫做
底边;两腰的夹角叫顶角,腰和底边的夹角叫底角。
A
B
C
腰
腰
底边
顶角
底角
底角
三角形三边之间的关系
它选择B—A路线,而不选择B—C—A路线,小狗的依据是什么?
C
B
A
两点之间,线段最短!
BC+AC>AB
同理可得:AC+AB>BC,AB+BC>AC
三角形任意两边之和大于第三边。
c
b
a
A
B
C
三角形三边之间的关系
如:a+b>c
a>c-b
c-b
三角形任意两边之和大于第三边。
有人说姚明一步能走4米
不可能
你相信吗?
课本P4【练习】 第2题
下列长度的三条线段能否组成三角形?
(1)3、4、8;(2)5、6、11;
(3)5、6、10
5. 已知a,b,c是三角形的三条边长,试化简:
6、长为10、7、5、3的四根木条,选其
中的三根组成三角形,有____种选法。
练:放风筝是中华民族的传统娱乐项目,小林为了做一个三角形风筝架,找到长度分别为3m和5m的两根木棍,那么他要寻找的第三根木棍a的长度的范围应是___________.
2m
(1)如果腰长是底长的2倍,那么各边的边长
是多少?
(2)能围成有一边的长是4 cm的等腰三角形吗?为什么?
例题讲解
1、如果等腰三角形的两边分别为4和6,
求它的周长。
变式:如果等腰三角形的两边分别为3和7,
求它的周长。
2、三角形三边的比为2:3:4,周长为36cm,
求三角形的边长。
综合练习(注意格式)
图中有几个三角形?
把它们一一写出来.
D
A
B
C
E
F
G
当堂训练
2、下列给出的三条线段不能组成三角形的是( )
A. 5cm,4cm,3cm
B.三条线段之比为2:3:5
C. 5m, 2m,6m
D.a=m+1,b=m+2,c=m+3(m>0)
B
3、若三角形的三边a、b、c 满足
|a-6|+(11-c)2+|6-b|=0,则△ABC是( )
A.不等边三角形 B.等腰三角形
C.等边三角形 D.以上答案都不对
B
当堂训练
4、长为10、7、5、3的四根木条,选其中的三根
组成三角形,有____种选法。
2
5、一个三角形两边长分别为3和7,
(1)第三边的长c的取值范围是___________;
(2)若第三边长为偶数,第三边长是_____________;
(3)三角形的周长p的取值范围是___________;
4
14
《基础小练习》P1-2
当堂检测
草原上的四口油井,位于如图所示的A、B、
C、D四个位置,现在要建立一个维修站H,
问H建在何处,才能使它到四个油井的距离之和HA+HB+HC+HD为最小?说明理由。
A
D
C
B
H
H′
拓展与应用
1、《全品》课时一
2、预习课本P4-5,完成P5练习(完成在课本上)
作业
