人教版八年级上册 第十一章 三角形 三角形的主要线段 (共23张PPT)
文档属性
| 名称 | 人教版八年级上册 第十一章 三角形 三角形的主要线段 (共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 487.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-07 00:00:00 | ||
图片预览




文档简介
(共23张PPT)
11.1.2三角形的线段
---高、中线与角平分线
1.理解三角形的高、中线和角平分线的概念,并能画出任意一个三角形的高、中线和角平分线;
2.能用数学语言表示三角形的高、中线和角平分线的定义,并应用其解答一些简单问题;
3.明确三角形的三条高的交点所在位置与三角形形状的关系。
学习目标
阅读课本P4-5,动手操作解决下面的问题
1.什么是三角形的高、中线、角平分线?注意概念,它们都是什么线?
2. 如何画高线?
3. 观察任意一个三角形的中线把大的三角形分成的两个小三角形,这两个小三角形面积有什么关系?为什么?
自学指导
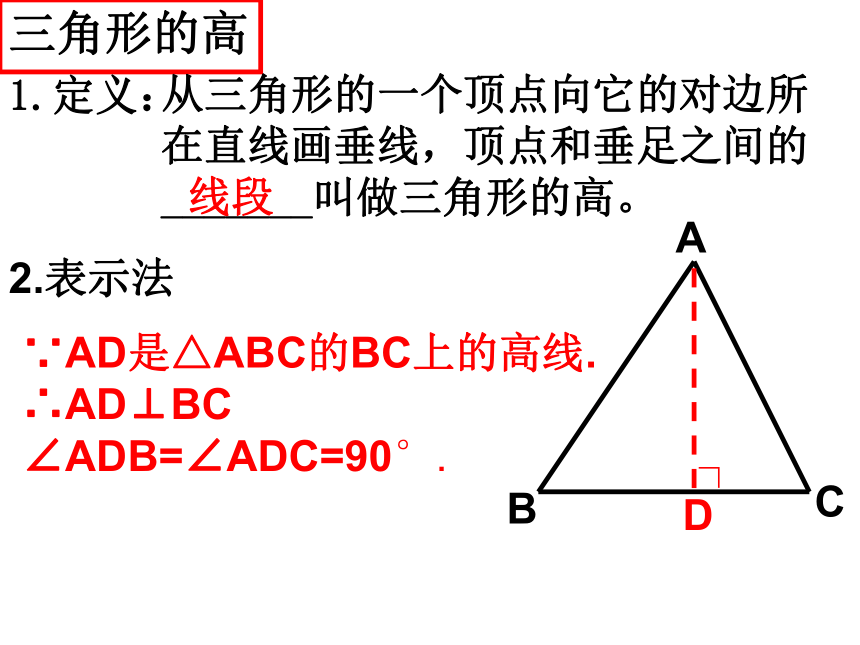
三角形的高
1.定义:
从三角形的一个顶点向它的对边所在直线画垂线,顶点和垂足之间的_______叫做三角形的高。
A
B
C
∟
D
线段
∵AD是△ABC的BC上的高线.
∴AD⊥BC
∠ADB=∠ADC=90°.
2.表示法
三角形的高
3.性质:
(1)三角形的高是一条_______;
(2) ①锐角三角形的三条高在三角形______,三条高的交点也在三角形_______。
内部
内部
②直角三角形的有两条高恰好是三角形的____
_______,另一条在三角形内部,它们的交点
在__________。
直角顶点
③钝角三角形有两条高恰好落在三角形的____,一条在三角形的_____,但三条高的_____交于
三角形____一点。
外部
内部
延长线
外
直角边
两条
线段
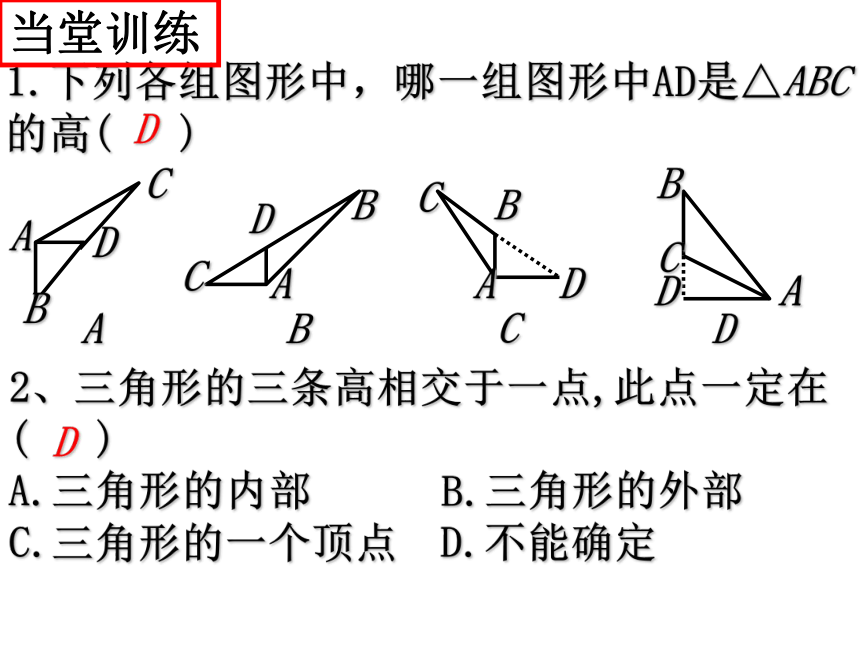
2、三角形的三条高相交于一点,此点一定在( )
A.三角形的内部 B.三角形的外部
C.三角形的一个顶点 D.不能确定
D
1.下列各组图形中,哪一组图形中AD是△ABC 的高( )
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
D
当堂训练
2.已知AD是△ABC的一条高,
∠BAD=70°∠CAD=20°,则∠BAC的度数为( )
A、50° B、60° C、90 D、50°或90°
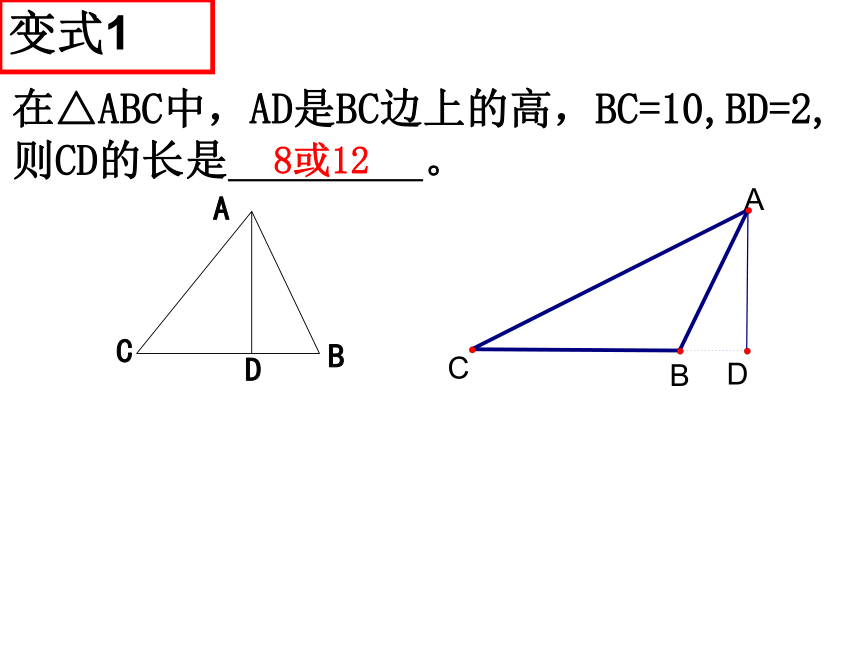
在△ABC中,AD是BC边上的高,BC=10,BD=2,则CD的长是 。
8或12
A
D
C
B
变式1
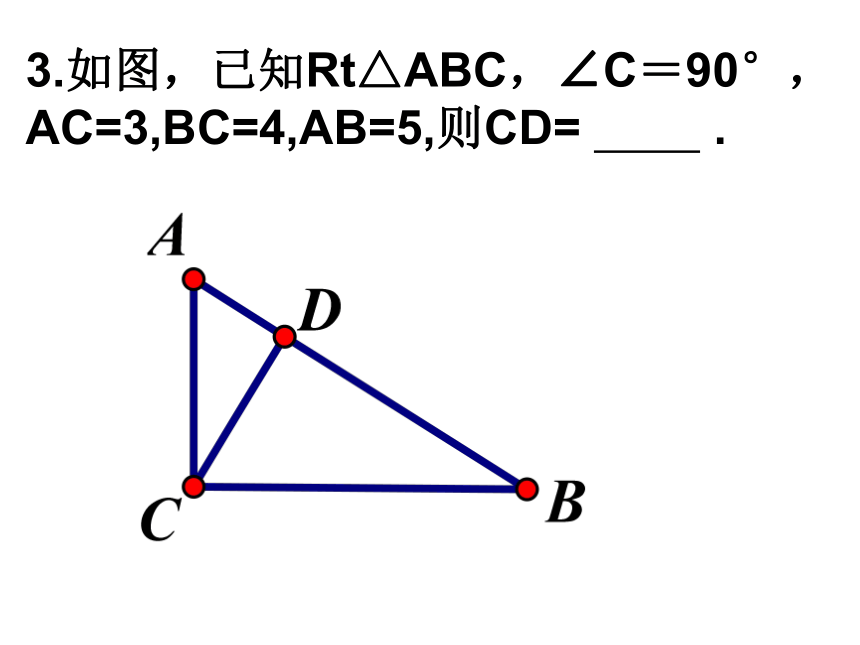
3.如图,已知Rt△ABC,∠C=90°,AC=3,BC=4,AB=5,则CD= .
4.如图,在△ABC中,AB=AC,D是BC上任意一点,过D分别向AB、AC作垂线,垂足分别为E,F,CG是AB边上的高,问DE,DF,CG间存在怎样的数量关系?
三角形的中线
1.定义:
在三角形中,连接一个顶点和它_________的线段叫做三角形的中线。
对边中点
A
B
C
D
∵ AD是△ABC的BC上的中线.
∴ BD=CD= BC.
2.表示法
(1)三角形三条中线相交于一点,
这点叫做三角形的( )且AO:DO= .
(2)三角形的一条中线将三角形分成的
两个三角形的面积 .
重心
2:1
相等
三角形的中线
3.性质:
(1)三角形的中线是一条______;
(2)三角形三条中线相交于三角形____一点;
注:三角形三条中线的交点叫做三角形的_____.
重心
线段
内
(3)三角形的中线分成的两个三角形的面积与周长的关系:____________________;
周长差等于另两边长的差
面积相等
____________________.
如图(1),AD,BE,CF是ΔABC的三条中线,则AB=2 ,BD= ,AE=_____。
AF
CD
AC
课本P5练习2(1)
1.如图,在△ABC中,点D、E、F分别
为BC、AD、CE的中点,且 =8cm2,
则 = .
2. 如图,AM、BN为中线,已知△ABO的面积为6,△BOM的面积为2,则四边形MCNO的面积为 。
3.如图,已知△ABC,现将边BA延长至点D,使AD=AB,延长AC至点E,使CE=2AC.延长CB至点F,使BF=3BC,分别连结DE,DF,EF,得到△DEF,若△DEF的面积为36,则阴影部分的面积和为_____________
三角形的角平分线
1.定义:
在三角形中,一个内角的平分线和对边相交,这个角的顶点与交点之间的_____叫做三角形的角平分线。
线段
A
B
C
D
2.表示法
∵AD是△ABC的∠BAC的平分线
∴∠1=∠2= ∠BAC
1
2
A
D
B
C
能力提高
1.在ΔABC中,CD是中线,已知BC-AC=5cm,
ΔDBC的周长为25cm,求ΔADC的周长.
A
B
D
C
能力提高
2.如图 在△ABC中AB=AC,周长为16厘米,
AC边上的中线BD将△ABC分成周长差为
2厘米的两个三角形,求△ABC的各边长。
C
D
E
O
F
A
B
能力提高
3.如图,AD是ΔABC的角平分线,DE∥AB,
DF∥AC,EF交AD于点O,
试问:OD是否是ΔEDF的角平分线?
如果是,请说明理由;如果不是,请举反例。
4.如图①,在△ABC 中,AD平分∠BAC,AE⊥BC,∠B=40°,∠C=70°.(1)求∠DAE的度数;
(2)如图②,若把“AE⊥BC”变成“点F在DA的延长线上,FE⊥BC”,其它条件不变,求∠DFE的度数.
作业
1.《全品》课时二
2.预习课本P6-7,完成课后P7练习
11.1.2三角形的线段
---高、中线与角平分线
1.理解三角形的高、中线和角平分线的概念,并能画出任意一个三角形的高、中线和角平分线;
2.能用数学语言表示三角形的高、中线和角平分线的定义,并应用其解答一些简单问题;
3.明确三角形的三条高的交点所在位置与三角形形状的关系。
学习目标
阅读课本P4-5,动手操作解决下面的问题
1.什么是三角形的高、中线、角平分线?注意概念,它们都是什么线?
2. 如何画高线?
3. 观察任意一个三角形的中线把大的三角形分成的两个小三角形,这两个小三角形面积有什么关系?为什么?
自学指导
三角形的高
1.定义:
从三角形的一个顶点向它的对边所在直线画垂线,顶点和垂足之间的_______叫做三角形的高。
A
B
C
∟
D
线段
∵AD是△ABC的BC上的高线.
∴AD⊥BC
∠ADB=∠ADC=90°.
2.表示法
三角形的高
3.性质:
(1)三角形的高是一条_______;
(2) ①锐角三角形的三条高在三角形______,三条高的交点也在三角形_______。
内部
内部
②直角三角形的有两条高恰好是三角形的____
_______,另一条在三角形内部,它们的交点
在__________。
直角顶点
③钝角三角形有两条高恰好落在三角形的____,一条在三角形的_____,但三条高的_____交于
三角形____一点。
外部
内部
延长线
外
直角边
两条
线段
2、三角形的三条高相交于一点,此点一定在( )
A.三角形的内部 B.三角形的外部
C.三角形的一个顶点 D.不能确定
D
1.下列各组图形中,哪一组图形中AD是△ABC 的高( )
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
D
当堂训练
2.已知AD是△ABC的一条高,
∠BAD=70°∠CAD=20°,则∠BAC的度数为( )
A、50° B、60° C、90 D、50°或90°
在△ABC中,AD是BC边上的高,BC=10,BD=2,则CD的长是 。
8或12
A
D
C
B
变式1
3.如图,已知Rt△ABC,∠C=90°,AC=3,BC=4,AB=5,则CD= .
4.如图,在△ABC中,AB=AC,D是BC上任意一点,过D分别向AB、AC作垂线,垂足分别为E,F,CG是AB边上的高,问DE,DF,CG间存在怎样的数量关系?
三角形的中线
1.定义:
在三角形中,连接一个顶点和它_________的线段叫做三角形的中线。
对边中点
A
B
C
D
∵ AD是△ABC的BC上的中线.
∴ BD=CD= BC.
2.表示法
(1)三角形三条中线相交于一点,
这点叫做三角形的( )且AO:DO= .
(2)三角形的一条中线将三角形分成的
两个三角形的面积 .
重心
2:1
相等
三角形的中线
3.性质:
(1)三角形的中线是一条______;
(2)三角形三条中线相交于三角形____一点;
注:三角形三条中线的交点叫做三角形的_____.
重心
线段
内
(3)三角形的中线分成的两个三角形的面积与周长的关系:____________________;
周长差等于另两边长的差
面积相等
____________________.
如图(1),AD,BE,CF是ΔABC的三条中线,则AB=2 ,BD= ,AE=_____。
AF
CD
AC
课本P5练习2(1)
1.如图,在△ABC中,点D、E、F分别
为BC、AD、CE的中点,且 =8cm2,
则 = .
2. 如图,AM、BN为中线,已知△ABO的面积为6,△BOM的面积为2,则四边形MCNO的面积为 。
3.如图,已知△ABC,现将边BA延长至点D,使AD=AB,延长AC至点E,使CE=2AC.延长CB至点F,使BF=3BC,分别连结DE,DF,EF,得到△DEF,若△DEF的面积为36,则阴影部分的面积和为_____________
三角形的角平分线
1.定义:
在三角形中,一个内角的平分线和对边相交,这个角的顶点与交点之间的_____叫做三角形的角平分线。
线段
A
B
C
D
2.表示法
∵AD是△ABC的∠BAC的平分线
∴∠1=∠2= ∠BAC
1
2
A
D
B
C
能力提高
1.在ΔABC中,CD是中线,已知BC-AC=5cm,
ΔDBC的周长为25cm,求ΔADC的周长.
A
B
D
C
能力提高
2.如图 在△ABC中AB=AC,周长为16厘米,
AC边上的中线BD将△ABC分成周长差为
2厘米的两个三角形,求△ABC的各边长。
C
D
E
O
F
A
B
能力提高
3.如图,AD是ΔABC的角平分线,DE∥AB,
DF∥AC,EF交AD于点O,
试问:OD是否是ΔEDF的角平分线?
如果是,请说明理由;如果不是,请举反例。
4.如图①,在△ABC 中,AD平分∠BAC,AE⊥BC,∠B=40°,∠C=70°.(1)求∠DAE的度数;
(2)如图②,若把“AE⊥BC”变成“点F在DA的延长线上,FE⊥BC”,其它条件不变,求∠DFE的度数.
作业
1.《全品》课时二
2.预习课本P6-7,完成课后P7练习
