高中数学必修第一册人教A版(2019) 4.3.2《对数的运算---习题课》名师课件(共31张PPT)
文档属性
| 名称 | 高中数学必修第一册人教A版(2019) 4.3.2《对数的运算---习题课》名师课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-06 19:50:47 | ||
图片预览



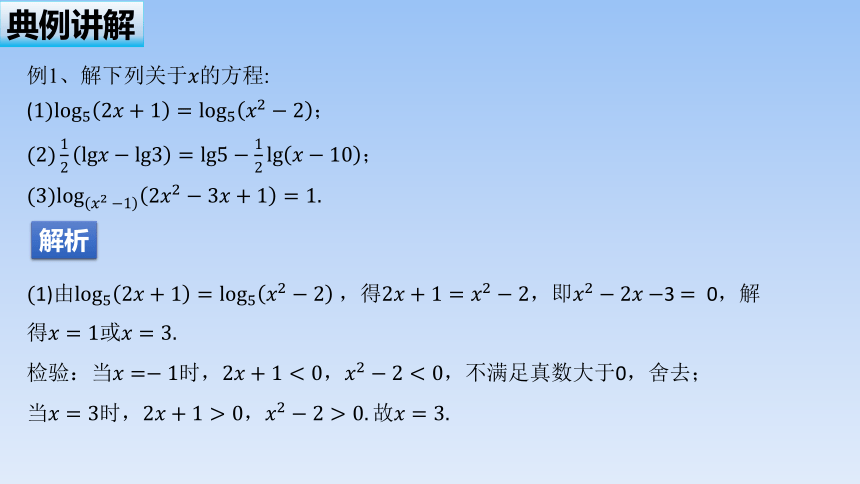








文档简介
(共31张PPT)
人教A版同步教材名师课件
对数的运算
---习题课
一、对数方程问题
二、带附加条件的指、对数问题
三、对数式与方程、不等式的综合应用
四、对数的实际应用
一、对数方程问题
典例讲解
例1、解下列关于的方程:
(;
;
解析
1)由,得,即3 0,解得或
检验:当时,,不满足真数大于0,舍去;
当时,
典例讲解
例1、解下列关于的方程:
(;
;
解析
2)根据题意得10.原方程可化为,
,即,解得
经检验,15是原方程的解.
典例讲解
例1、解下列关于的方程:
(;
;
解析
(3)原方程可化为,
,即2 0,解得
检验:当时,,不满足底数大于0且不等于1,舍去;
当时,
方法归纳
对数方程的题型与解法如下:
将对数式转化为指数式
转化为必须验根)
) 换元,另,,转化为关于的方程
题型
解法
在进行对数运算变形时,一定要注意变形前后未知数的范围有没有发生变化,避免产生多解或漏解的错误.
变式训练
1.方程( )
2
由真数大于0,易得>1,原方程可化为
解析
典例讲解
例2、解下列关于 的方程:
(
解析
(1)原方程可化为
即5)( )=0,所以=2,解得.
经检验知,都是原方程的解.
(2)由题意得,,原方程可化为,
化简,得解得10和
经检验知,都是原方程的解.
方法归纳
在求解含有对数式的问题时,一定要注意真数的取值范围,保证真数大于零.求解过程不等价时,在求出答案后需进行检验.
变式训练
2.解方程:
则 ,
,两边取以10为底的对数,
得,= ±1,
解得10或
经检验,都是原方程的解.
解析
二、带附加条件的指、对数问题
典例讲解
例3、,求值.
(2)已知=, 7,用, 表示
解析
(
(
思路分析
, .
典例讲解
例3、,求值.
(2)已知=, 7,用, 表示
解析
(1)
(2)
思路分析
(2)
方法归纳
①在求解过程中,根据问题的需要,将指数式转化为对数式或将对数式转化为指数式,这是数学转化思想的具体表现.
②对数运算就是指数运算的逆运算因此,当一个题目中同时出现指数式和对数式时,一般要把问题转化、统一为一种表达形式.
变式训练
3.(1)已知
(2)已知
(1)由得,
.
(2)
解析
典例讲解
例4、已知为,,为正数,且
(1)求使2=成立的的值;
(2)求证: .
思路分析
=>1,则
(1)由2=得,因为
(2)证明: .
解析
遇到连等形式的问题,一般统一赋值,再利用指数式与对数式的互化原则进行转化.
方法归纳
解决指数恒等式问题的方法:
通过引入对数式,将互相不便转化运用的条件有机地联系在一起,尤其是换底公式的运用,使得条件之间的内在关系显现出来,问题求解也就顺理成章了.
变式训练
4. (1)已知.
(2)已知,求实数得值.
(1)证明:由.
解析
变式训练
4. (1)已知.
(2)已知,求实数得值.
解析
(2)因为
所以
因为
典例讲解
例5、已知
思路分析
因为所以
所以
.
解析
先把已知式子转化为的形式,再确定的关系.
方法归纳
带有附加条件的对数式或指数式的求值问题,需要对已知条件和所求式子进行化简转化,原则是化为同底的对数,以便利用对数的运算性质要整体把握对数式的结构特征,灵活进行指数式与对数式的互化.
变式训练
5.已知值.
由
解析
三、对数式与方程、不等式的综合应用
典例讲解
思路分析
原方程可化为
设= ,则原方程可化为,
所以.
解析
因为是方程的两个实根,所以可分析出、 是方程的两根,再利用根与系数的关系求出+、 · 的值即可求解.
典例讲解
解析
又因为
所以.
所以
即
方法归纳
对数知识常常与其他知识交汇在一起,构成较复杂的题目,如此题与方程综合.在求解这样的题目时,灵活运用对数的运算性质就可以使问题得到解决.
变式训练
6.方程两根的积等于 ( )
因为
所以
解析
典例讲解
思路分析
(1)根据题目中条件“光线通过一块玻璃,其强度要损失10%”分析出关于的关系式;
(2)根据条件“减弱到原来的以下”建立不等关系进行求解.
例7、已知光线通过一块玻璃,其强度要损失10%,设光线原来的强度为 ( 为正常数),通过 块玻璃以后的强度为 .
解析
(1)光线通过块玻璃后的强度为所以.
(2)由题意得由
又
至少通过11块玻璃以后,光线强度减弱到原来的以下.
方法归纳
对数运算在实际生产和科学研究中应用广泛,其应用问题大致可以分为两类:
(1)建立对数式,在此基础上进行一些实际求值,计算时要注意指数式与对数式的互化;
(2)建立指数函数型应用模型,再进行指数求值,此时往往将等式两边同时取对数进行计算.
变式训练
7.有关数据显示,中国快递行业产生的包装垃圾在2015年约为400万吨,2016年的年增长率为50%,有专家预测,如果不采取措施,未来包装垃圾还将以此增长率增长,从______年开始,快递行业产生的包装垃圾超过4000万吨.(参考数据:g2≈0.3010,lg3≈0.4771)
设快递行业产生的包装垃圾为万吨,表示从2015年开始增加的年份的数量.
由题意可得
两边取以10为底的对数并化简可得=1
∴(0.4771-0.3010)=1,即0.1761=1又, ∴ n=6,∴2015+6=2021.
故从2021年开始,快递行业产生的包装垃圾超过4000万吨.
解析
人教A版同步教材名师课件
对数的运算
---习题课
一、对数方程问题
二、带附加条件的指、对数问题
三、对数式与方程、不等式的综合应用
四、对数的实际应用
一、对数方程问题
典例讲解
例1、解下列关于的方程:
(;
;
解析
1)由,得,即3 0,解得或
检验:当时,,不满足真数大于0,舍去;
当时,
典例讲解
例1、解下列关于的方程:
(;
;
解析
2)根据题意得10.原方程可化为,
,即,解得
经检验,15是原方程的解.
典例讲解
例1、解下列关于的方程:
(;
;
解析
(3)原方程可化为,
,即2 0,解得
检验:当时,,不满足底数大于0且不等于1,舍去;
当时,
方法归纳
对数方程的题型与解法如下:
将对数式转化为指数式
转化为必须验根)
) 换元,另,,转化为关于的方程
题型
解法
在进行对数运算变形时,一定要注意变形前后未知数的范围有没有发生变化,避免产生多解或漏解的错误.
变式训练
1.方程( )
2
由真数大于0,易得>1,原方程可化为
解析
典例讲解
例2、解下列关于 的方程:
(
解析
(1)原方程可化为
即5)( )=0,所以=2,解得.
经检验知,都是原方程的解.
(2)由题意得,,原方程可化为,
化简,得解得10和
经检验知,都是原方程的解.
方法归纳
在求解含有对数式的问题时,一定要注意真数的取值范围,保证真数大于零.求解过程不等价时,在求出答案后需进行检验.
变式训练
2.解方程:
则 ,
,两边取以10为底的对数,
得,= ±1,
解得10或
经检验,都是原方程的解.
解析
二、带附加条件的指、对数问题
典例讲解
例3、,求值.
(2)已知=, 7,用, 表示
解析
(
(
思路分析
, .
典例讲解
例3、,求值.
(2)已知=, 7,用, 表示
解析
(1)
(2)
思路分析
(2)
方法归纳
①在求解过程中,根据问题的需要,将指数式转化为对数式或将对数式转化为指数式,这是数学转化思想的具体表现.
②对数运算就是指数运算的逆运算因此,当一个题目中同时出现指数式和对数式时,一般要把问题转化、统一为一种表达形式.
变式训练
3.(1)已知
(2)已知
(1)由得,
.
(2)
解析
典例讲解
例4、已知为,,为正数,且
(1)求使2=成立的的值;
(2)求证: .
思路分析
=>1,则
(1)由2=得,因为
(2)证明: .
解析
遇到连等形式的问题,一般统一赋值,再利用指数式与对数式的互化原则进行转化.
方法归纳
解决指数恒等式问题的方法:
通过引入对数式,将互相不便转化运用的条件有机地联系在一起,尤其是换底公式的运用,使得条件之间的内在关系显现出来,问题求解也就顺理成章了.
变式训练
4. (1)已知.
(2)已知,求实数得值.
(1)证明:由.
解析
变式训练
4. (1)已知.
(2)已知,求实数得值.
解析
(2)因为
所以
因为
典例讲解
例5、已知
思路分析
因为所以
所以
.
解析
先把已知式子转化为的形式,再确定的关系.
方法归纳
带有附加条件的对数式或指数式的求值问题,需要对已知条件和所求式子进行化简转化,原则是化为同底的对数,以便利用对数的运算性质要整体把握对数式的结构特征,灵活进行指数式与对数式的互化.
变式训练
5.已知值.
由
解析
三、对数式与方程、不等式的综合应用
典例讲解
思路分析
原方程可化为
设= ,则原方程可化为,
所以.
解析
因为是方程的两个实根,所以可分析出、 是方程的两根,再利用根与系数的关系求出+、 · 的值即可求解.
典例讲解
解析
又因为
所以.
所以
即
方法归纳
对数知识常常与其他知识交汇在一起,构成较复杂的题目,如此题与方程综合.在求解这样的题目时,灵活运用对数的运算性质就可以使问题得到解决.
变式训练
6.方程两根的积等于 ( )
因为
所以
解析
典例讲解
思路分析
(1)根据题目中条件“光线通过一块玻璃,其强度要损失10%”分析出关于的关系式;
(2)根据条件“减弱到原来的以下”建立不等关系进行求解.
例7、已知光线通过一块玻璃,其强度要损失10%,设光线原来的强度为 ( 为正常数),通过 块玻璃以后的强度为 .
解析
(1)光线通过块玻璃后的强度为所以.
(2)由题意得由
又
至少通过11块玻璃以后,光线强度减弱到原来的以下.
方法归纳
对数运算在实际生产和科学研究中应用广泛,其应用问题大致可以分为两类:
(1)建立对数式,在此基础上进行一些实际求值,计算时要注意指数式与对数式的互化;
(2)建立指数函数型应用模型,再进行指数求值,此时往往将等式两边同时取对数进行计算.
变式训练
7.有关数据显示,中国快递行业产生的包装垃圾在2015年约为400万吨,2016年的年增长率为50%,有专家预测,如果不采取措施,未来包装垃圾还将以此增长率增长,从______年开始,快递行业产生的包装垃圾超过4000万吨.(参考数据:g2≈0.3010,lg3≈0.4771)
设快递行业产生的包装垃圾为万吨,表示从2015年开始增加的年份的数量.
由题意可得
两边取以10为底的对数并化简可得=1
∴(0.4771-0.3010)=1,即0.1761=1又, ∴ n=6,∴2015+6=2021.
故从2021年开始,快递行业产生的包装垃圾超过4000万吨.
解析
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
