高中数学必修第一册人教A版(2019) 4.3.2 对数的运算 导学案(含答案)
文档属性
| 名称 | 高中数学必修第一册人教A版(2019) 4.3.2 对数的运算 导学案(含答案) | 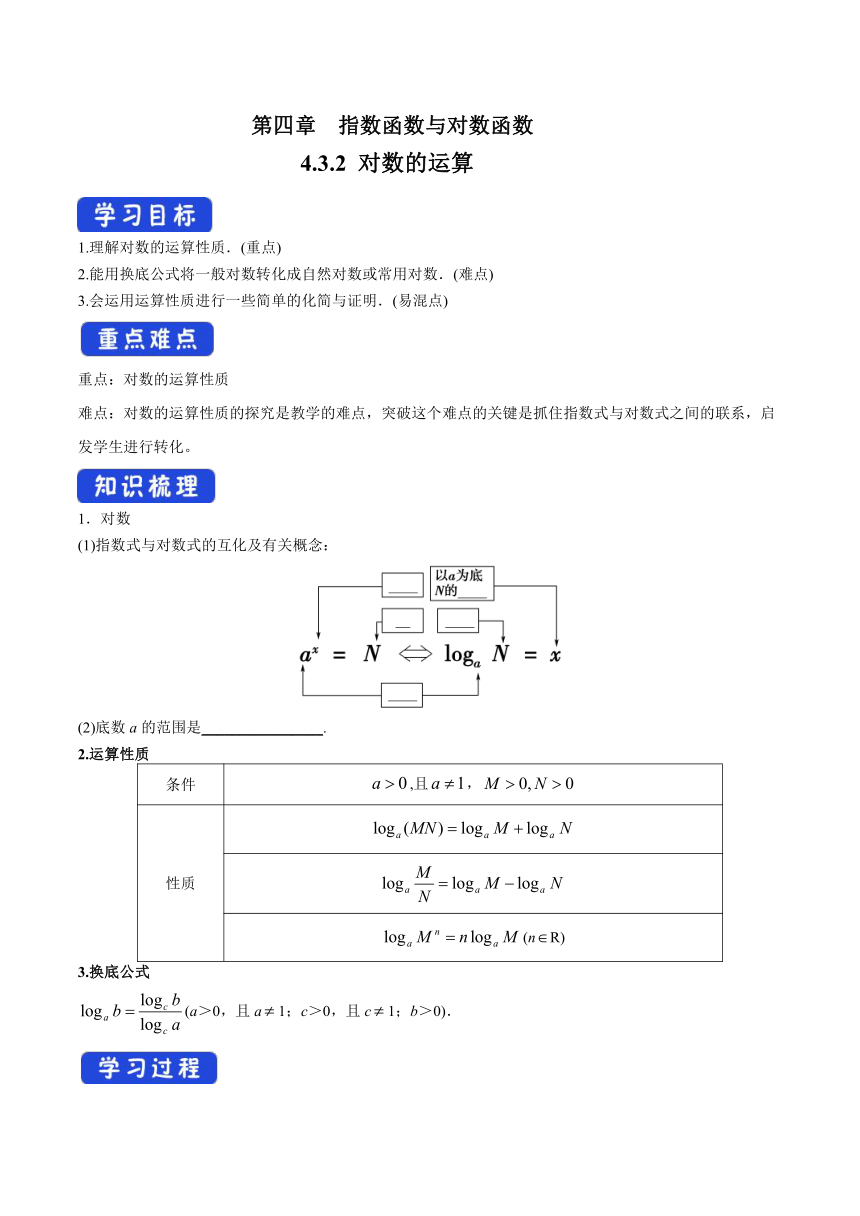 | |
| 格式 | docx | ||
| 文件大小 | 207.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-06 22:51:10 | ||
图片预览


文档简介
第四章 指数函数与对数函数
4.3.2 对数的运算
1.理解对数的运算性质.(重点)
能用换底公式将一般对数转化成自然对数或常用对数.(难点)
3.会运用运算性质进行一些简单的化简与证明.(易混点)
重点:对数的运算性质
难点:对数的运算性质的探究是教学的难点,突破这个难点的关键是抓住指数式与对数式之间的联系,启发学生进行转化。
1.对数
(1)指数式与对数式的互化及有关概念:
(2)底数a的范围是________________.
2.运算性质
条件 ,且,
性质
(nR)
3.换底公式
(a>0,且a1;c>0,且c1;b>0).
问题提出:在引入对数之后,自然应研究对数的运算性质.你认为可以怎样研究?
我们知道了对数与指数间的关系,能否利用指数幂运算性质得出相应的对数运算性质呢?
探究一:对数的运算性质
回顾指数幂的运算性质:
,,.
把指对数互化的式子具体化:
设,,
于是有.
根据对数的定义有:,,.
于是有对数的运算性质:
如果,且时,M>0,N>0,那么:
(1) ;(积的对数等于两对数的和)
(2) ;(商的对数等于两对数的差)
(3) ;().(幂的对数等于幂指数乘以底数的对数)
1.思考辨析
(1)积、商的对数可以化为对数的和、差.( )
(2)loga(xy)=logax·logay.( )
(3)log2(-3)2=2log2(-3).( )
例1.求下列各式的值
(1)log84+log82;(2)log510-log52 (3)log2(47×25)
跟踪训练1 计算下列各式的值:
(1)lg -lg +lg ;
(2)lg 52+lg 8+lg 5·lg 20+(lg 2)2;
(3).
探究二:换底公式
问题1:前面我们学习了常用对数和自然对数,我们知道任意不等于1的正数都可以作为对数的底,能否将其它底的对数转换为以10或为底的对数?
把问题一般化,能否把以为底转化为以为底?
探究:设,则,对此等式两边取以为底的对数,得到:
,根据对数的性质,有:,所以.
即.其中,且,,且.
公式 ;称为换底公式.
用换底公式可以很方便地利用计算器进行对数的数值计算.
问题2:在4.2.1的问题1中,求经过多少年B地景区的游客人次是2001年的2倍,就是计算 2 的值。
例3.尽管目前人类还无法准确预报地震,但科学家通过研究,已经对地震有所了解,例如,地震时释放出的能量E(单位:焦耳)与地震里氏震M之间的关系为
2011年3月11日,日本东北部海域发生里氏9.0级地震,它所释放出来的能量是2008年5月12日我国汶川发生里氏8.0级地震的多少倍(精确到1)?
跟踪训练2求值:
(1)log23·log35·log516; (2)(log32+log92)(log43+log83).
1.计算:log153-log62+log155-log63=( )
A.-2 B.0 C.1 D.2
2.计算log92·log43=( )
A.4 B.2 C. D.
3.设10a=2,lg 3=b,则log26=( )
A. B. C.ab D.a+b
4. log816=________.
5.计算:(1)log535-2log5+log57-log51.8;
(2)log2+log212-log242-1.
1.对数的运算法则。
2.利用定义及指数运算证明对数的运算法则。
3.对数运算法则的应用。
4.换底公式的证明及应用。
参考答案:
二、学习过程
思考辨析 1. [答案] (1)√ (2)× (3)×
例1.解:(1)log84+log82=log88=1.
(2)log510-log52=log55=1
(3) log2(47×25)= log2219 =19
跟踪训练1[解] (1)原式=(5lg 2-2lg 7)-·lg 2+(2lg 7+lg 5)
=lg 2-lg 7-2lg 2+lg 7+lg 5
=lg 2+lg 5=(lg 2+lg 5)=lg 10=.
(2)原式=2lg 5+2lg 2+lg 5(2lg 2+lg 5)+(lg 2)2
=2lg 10+(lg 5+lg 2)2=2+(lg 10)2=2+1=3.
(3)原式====.
例2.[解]
问题2:换底公式可得2=,
利用计算工具,可得=,
由此可得,大约经过7年,B地景区的
游客人次就达到2001年的2倍,类似地,可以求出游客人次是2001年的3倍,4倍,:…所需要的年数。
例3解:设里氏9.0级和里氏8.0级地震的能量分别为E1和E2
设里利用计算工具可得,
虽然里氏9.0级和里氏8.0级地震仅相差1级,但前者释放出的能量却是后者的约32倍。
跟踪训练2.[解] (1)原式=··===4.
(2)原式=
==·=..
三、达标检测
1.【答案】B [原式=log15(3×5)-log6(2×3)=1-1=0.]
2.【答案】D [log92·log43=·=.]
3.【答案】B [∵10a=2,∴lg 2=a,
∴log26===.]
4.【答案】 [log816=log2324=.]
5【答案】(1)原式=log5(5×7)-2(log57-log53)+log57-log5
=log55+log57-2log57+2log53+log57-2log53+log55=2.
(2)原式=log2+log212-log2-log22
=log2=log2=log22=-.
4.3.2 对数的运算
1.理解对数的运算性质.(重点)
能用换底公式将一般对数转化成自然对数或常用对数.(难点)
3.会运用运算性质进行一些简单的化简与证明.(易混点)
重点:对数的运算性质
难点:对数的运算性质的探究是教学的难点,突破这个难点的关键是抓住指数式与对数式之间的联系,启发学生进行转化。
1.对数
(1)指数式与对数式的互化及有关概念:
(2)底数a的范围是________________.
2.运算性质
条件 ,且,
性质
(nR)
3.换底公式
(a>0,且a1;c>0,且c1;b>0).
问题提出:在引入对数之后,自然应研究对数的运算性质.你认为可以怎样研究?
我们知道了对数与指数间的关系,能否利用指数幂运算性质得出相应的对数运算性质呢?
探究一:对数的运算性质
回顾指数幂的运算性质:
,,.
把指对数互化的式子具体化:
设,,
于是有.
根据对数的定义有:,,.
于是有对数的运算性质:
如果,且时,M>0,N>0,那么:
(1) ;(积的对数等于两对数的和)
(2) ;(商的对数等于两对数的差)
(3) ;().(幂的对数等于幂指数乘以底数的对数)
1.思考辨析
(1)积、商的对数可以化为对数的和、差.( )
(2)loga(xy)=logax·logay.( )
(3)log2(-3)2=2log2(-3).( )
例1.求下列各式的值
(1)log84+log82;(2)log510-log52 (3)log2(47×25)
跟踪训练1 计算下列各式的值:
(1)lg -lg +lg ;
(2)lg 52+lg 8+lg 5·lg 20+(lg 2)2;
(3).
探究二:换底公式
问题1:前面我们学习了常用对数和自然对数,我们知道任意不等于1的正数都可以作为对数的底,能否将其它底的对数转换为以10或为底的对数?
把问题一般化,能否把以为底转化为以为底?
探究:设,则,对此等式两边取以为底的对数,得到:
,根据对数的性质,有:,所以.
即.其中,且,,且.
公式 ;称为换底公式.
用换底公式可以很方便地利用计算器进行对数的数值计算.
问题2:在4.2.1的问题1中,求经过多少年B地景区的游客人次是2001年的2倍,就是计算 2 的值。
例3.尽管目前人类还无法准确预报地震,但科学家通过研究,已经对地震有所了解,例如,地震时释放出的能量E(单位:焦耳)与地震里氏震M之间的关系为
2011年3月11日,日本东北部海域发生里氏9.0级地震,它所释放出来的能量是2008年5月12日我国汶川发生里氏8.0级地震的多少倍(精确到1)?
跟踪训练2求值:
(1)log23·log35·log516; (2)(log32+log92)(log43+log83).
1.计算:log153-log62+log155-log63=( )
A.-2 B.0 C.1 D.2
2.计算log92·log43=( )
A.4 B.2 C. D.
3.设10a=2,lg 3=b,则log26=( )
A. B. C.ab D.a+b
4. log816=________.
5.计算:(1)log535-2log5+log57-log51.8;
(2)log2+log212-log242-1.
1.对数的运算法则。
2.利用定义及指数运算证明对数的运算法则。
3.对数运算法则的应用。
4.换底公式的证明及应用。
参考答案:
二、学习过程
思考辨析 1. [答案] (1)√ (2)× (3)×
例1.解:(1)log84+log82=log88=1.
(2)log510-log52=log55=1
(3) log2(47×25)= log2219 =19
跟踪训练1[解] (1)原式=(5lg 2-2lg 7)-·lg 2+(2lg 7+lg 5)
=lg 2-lg 7-2lg 2+lg 7+lg 5
=lg 2+lg 5=(lg 2+lg 5)=lg 10=.
(2)原式=2lg 5+2lg 2+lg 5(2lg 2+lg 5)+(lg 2)2
=2lg 10+(lg 5+lg 2)2=2+(lg 10)2=2+1=3.
(3)原式====.
例2.[解]
问题2:换底公式可得2=,
利用计算工具,可得=,
由此可得,大约经过7年,B地景区的
游客人次就达到2001年的2倍,类似地,可以求出游客人次是2001年的3倍,4倍,:…所需要的年数。
例3解:设里氏9.0级和里氏8.0级地震的能量分别为E1和E2
设里利用计算工具可得,
虽然里氏9.0级和里氏8.0级地震仅相差1级,但前者释放出的能量却是后者的约32倍。
跟踪训练2.[解] (1)原式=··===4.
(2)原式=
==·=..
三、达标检测
1.【答案】B [原式=log15(3×5)-log6(2×3)=1-1=0.]
2.【答案】D [log92·log43=·=.]
3.【答案】B [∵10a=2,∴lg 2=a,
∴log26===.]
4.【答案】 [log816=log2324=.]
5【答案】(1)原式=log5(5×7)-2(log57-log53)+log57-log5
=log55+log57-2log57+2log53+log57-2log53+log55=2.
(2)原式=log2+log212-log2-log22
=log2=log2=log22=-.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
