任意角
图片预览









文档简介
课件41张PPT。1.1.1任意角(一)晨 景日出日落,寒来暑往……自然界中有许多“按一定规律周而复始”的现象,我们能用什么样的数学模型来刻画?花样游泳中,运动员旋转的周数如何
用角度计算来表示?
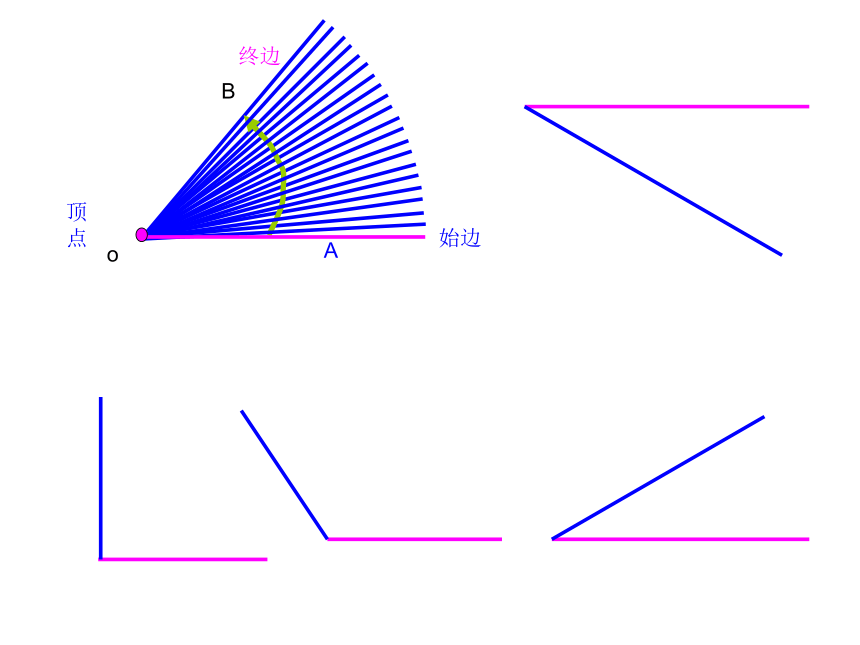
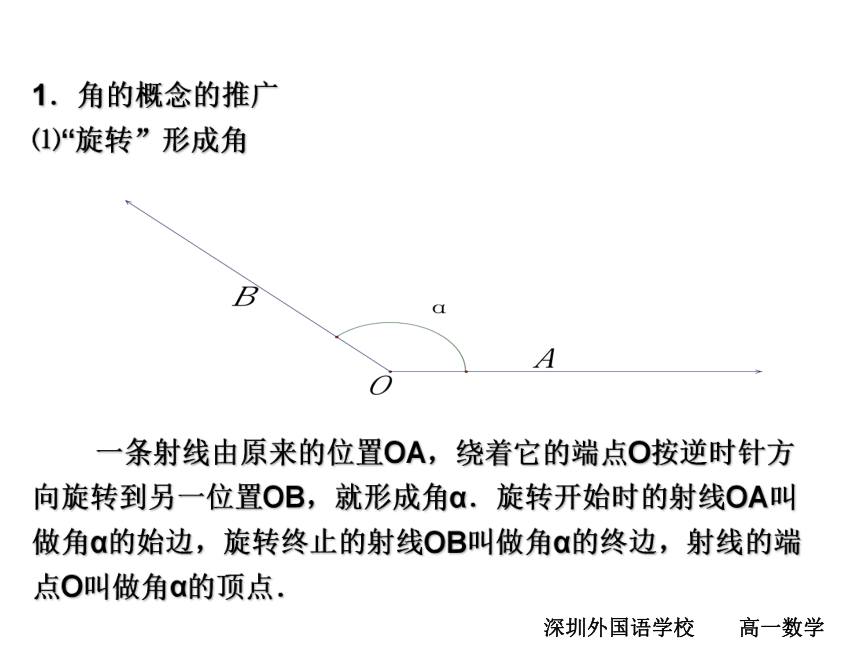
oAB始边 终边顶点一、复习基础知识1、角的定义:定义1:从一点出发的两条射线所组成的图形角的范围:~定义2:平面内一条射线绕着端点从一个位置
旋转到另一个位置所形成的图形。2、角的表示:简记:1.角的概念的推广
⑴“旋转”形成角
一条射线由原来的位置OA,绕着它的端点O按逆时针方向旋转到另一位置OB,就形成角α.旋转开始时的射线OA叫做角α的始边,旋转终止的射线OB叫做角α的终边,射线的端点O叫做角α的顶点.深圳外国语学校 高一数学二、新学思考下面的角度如何表示?(1)你的手表慢了5分钟,想将它校准,分针应该旋转多少度?(2)假如你的手表快了2.5小时,想将它校准,分针应该旋转多少度?1.规定:正角:按逆时针方向旋转形成的角负角:按顺时针方向旋转形成的角 零角:一条射线没有作任何旋转时形成的角任意角终边与始边重合的角是零角吗?二、新学思考下面的角度如何表示?(1)你的手表慢了5分钟,想将它校准,分针应该旋转多少度?(2)假如你的手表快了2.5小时,想将它校准,分针应该旋转多少度?-30°900°二、探究新知观察思考:比较下面这几个角:210°210°210°你发现了什么问题?xyo 1)置角的顶点于原点终边落在第几象限就是第几象限角2)始边重合于X轴的非负半轴
二、探究新知始边终边1)角的顶点与原点重合;2)角的始边与x轴的非负半轴重合.象限角:角的终边(除端点外)在第几象限就说这个角是第几象限角。非象限角:角的终边落在坐标轴上. 不属于任何象限。规定:·二、探究新知二、探究新知考考你:1.锐角是第几象限角?第一象限角都是锐角吗?
请你举例说明。2.请你说出下面的角是第几象限角:
(1)420°(2)-75°(3)3600° 在坐标系中的角
条件:(1)角的顶点与坐标原点重合象限角:角的终边(除端点外)在第几象限
就说这个角是第几象限角
终边在坐标轴上的角---不属于任何象限(2)始边于X轴的非负半轴重合二、探究新知知识小结2:思考:如果角的终边在第几象限,我们就说这个角是第几象限的角;如果角的终边在坐标轴上,就认为这个角不属于任何象限,或称这个角为轴上角.那么下列各角:
-50°,405°,210°,
-200°,-450°分别是第几象限的角?-450°请在坐标轴上画出-32°,328°,-392°,并找出它们的共同点?3280=-320+3600-3920=-320-3600=-320+1x3600 =-320-1x3600 -320= =-320+0x3600-320+2x3600 , -320-2x3600 -320+3x3600 , -320-3x3600 … , … ,与-320终边相同的角的一般形式为
-320+k 3600,K ∈ Z与α终边相同的角的一般形式为α+k 3600,K ∈ ZS={ β| β= α+k 3600 , K∈ Z}3、与角 终边相同
的角的表示:二、探究新知考考你:1.说出与30°终边相同的角的一般形式。2.在与30°终边相同的角中有几个角属于二、探究新知知识小结3:所有与角α终边相同的角,连同角α在内可构成一个集合
S={β|β=k·360°+α,k∈Z}
即任一与角α终边相同的角,都可以表示成α与整数个周角的和. 三、实践运用例1:在0°到360°范围内,分别找出与640°终边相同的角,并判定它们是第几象限。
当k=-1时我们得到角 280°,
所以与640°角终边相同的角是280°角,它是第四象限角;
解:与640°终边相同的角可以写成k·360°+640°第二象限第一象限第三象限典型例题合作探究课本上的例1:
在0到360度内找与已知角终边相同的角,方法是:用所给角除以3600 , 若所给角是正的,按通常的除法进行;所给角是负的,角度除以3600,商是负数,它的绝对值应比被除数为其相反数时相应的商大1,以便使余数为正值。例1 在0°~360°范围内,找出与-950°12′角终边相同的角并判定它是第几象限角: 解 : ∵-950°12′= 129048′-3×3600, ∴在0°~360°范围内, 与-950°12′角终边相同的角是129°48′, 它是第二象限角.例2 写出终边落在y轴上的角的集合。终边落在坐标轴上的情形0090018002700 + k?360° + k?360° + k?360° + k?360° 或3600+ k?360° 例2 写出终边落在y轴上的角的集合。解:在0°~360°范围内,在终边在y轴上的角有两个,90°,270°S1={β| β=900+K?3600,K∈Z} ={β| β=900+2K?1800,K∈Z}∴与270°角终边相同的角构成的集合S2={β| β=2700+K?3600,K∈Z}
={β| β=900+1800+2K?1800,K∈Z}
∪{β| β=900+(2K+1)1800 ,K∈Z}
S=S1∪S2所以 终边落在y轴上的角的集合为={β| β=900+K?1800 ,K∈Z}
{偶数}∪{奇数}={整数}∴与90°角终边相同的角构成的集合课堂小结:
终边在x轴正半轴上的角的集合:{?|?=k?360?, k?Z};
终边在x轴负半轴上的角的集合:{?|?=k?360?+180?,k?Z};
终边在x轴上的角的集合:{?|?=k?180?,k?Z};
终边在y轴正半轴上的角的集合:{?|?=k?360?+90?,k?Z};
终边在y轴负半轴上的角的集合:{?|?=k?360?+270?,k?Z};
终边在y轴上的角的集合:{?|?=k?180?+90?,k?Z};
终边在坐标轴上的角的集合:{?|?=k?90?,k?Z}.终边落在坐标轴上的情形0090018002700 + k?360° + k?360° + k?360° + k?360° 或3600+ k?360° 合作探究第一象限角的集合:
S={β/ 0o+K·360o< β < 90o+K·360o,K∈Z};
第二象限角的集合:
S={β/ 90o+K·360o< β < 180o+K·360o,K∈Z};
第三象限角的集合:
S={β/ 180o+K·360o< β < 270o+K·360o,K∈Z};第四象限角的集合:
S={β/ 270o+K·360o< β < 360o+K·360o,K∈Z};例4.如果 是第三象限角,那么2 角终边的位置如
何? 是哪个象限的角?解:利用上述方法判断,可得如下结论:12341234S={α|α=45°+k·180°,k∈Z}.-315°,-135°,45°,225°,405°,585°. 解: 例3 写出终边在直线y=x上的角的集合S,并把S中适合不等式-360°≤ <720°的元素写出来. 四、练习提高1.下列命题中正确的是
(A)第一象限角一定不是负角
(B)小于 的角一定是锐角
(C) 钝角一定是第二象限角
(D)第一象限角一定是锐角2.分针在1小时内所转过的角度是 ;时针转过的角度是 .
3.分别作出下列各角的终边,并指出它们
是第几象限角:4.下列各命题:
(1)相等的角终边一定相同;(2)终边相同的角一定相等;(3)第二象限的角一定大于第一象限任意一个角;(4)若 , 则 必是第一或第二象限角
其中正确的有 ( )练习例7C练习例11
用角度计算来表示?
oAB始边 终边顶点一、复习基础知识1、角的定义:定义1:从一点出发的两条射线所组成的图形角的范围:~定义2:平面内一条射线绕着端点从一个位置
旋转到另一个位置所形成的图形。2、角的表示:简记:1.角的概念的推广
⑴“旋转”形成角
一条射线由原来的位置OA,绕着它的端点O按逆时针方向旋转到另一位置OB,就形成角α.旋转开始时的射线OA叫做角α的始边,旋转终止的射线OB叫做角α的终边,射线的端点O叫做角α的顶点.深圳外国语学校 高一数学二、新学思考下面的角度如何表示?(1)你的手表慢了5分钟,想将它校准,分针应该旋转多少度?(2)假如你的手表快了2.5小时,想将它校准,分针应该旋转多少度?1.规定:正角:按逆时针方向旋转形成的角负角:按顺时针方向旋转形成的角 零角:一条射线没有作任何旋转时形成的角任意角终边与始边重合的角是零角吗?二、新学思考下面的角度如何表示?(1)你的手表慢了5分钟,想将它校准,分针应该旋转多少度?(2)假如你的手表快了2.5小时,想将它校准,分针应该旋转多少度?-30°900°二、探究新知观察思考:比较下面这几个角:210°210°210°你发现了什么问题?xyo 1)置角的顶点于原点终边落在第几象限就是第几象限角2)始边重合于X轴的非负半轴
二、探究新知始边终边1)角的顶点与原点重合;2)角的始边与x轴的非负半轴重合.象限角:角的终边(除端点外)在第几象限就说这个角是第几象限角。非象限角:角的终边落在坐标轴上. 不属于任何象限。规定:·二、探究新知二、探究新知考考你:1.锐角是第几象限角?第一象限角都是锐角吗?
请你举例说明。2.请你说出下面的角是第几象限角:
(1)420°(2)-75°(3)3600° 在坐标系中的角
条件:(1)角的顶点与坐标原点重合象限角:角的终边(除端点外)在第几象限
就说这个角是第几象限角
终边在坐标轴上的角---不属于任何象限(2)始边于X轴的非负半轴重合二、探究新知知识小结2:思考:如果角的终边在第几象限,我们就说这个角是第几象限的角;如果角的终边在坐标轴上,就认为这个角不属于任何象限,或称这个角为轴上角.那么下列各角:
-50°,405°,210°,
-200°,-450°分别是第几象限的角?-450°请在坐标轴上画出-32°,328°,-392°,并找出它们的共同点?3280=-320+3600-3920=-320-3600=-320+1x3600 =-320-1x3600 -320= =-320+0x3600-320+2x3600 , -320-2x3600 -320+3x3600 , -320-3x3600 … , … ,与-320终边相同的角的一般形式为
-320+k 3600,K ∈ Z与α终边相同的角的一般形式为α+k 3600,K ∈ ZS={ β| β= α+k 3600 , K∈ Z}3、与角 终边相同
的角的表示:二、探究新知考考你:1.说出与30°终边相同的角的一般形式。2.在与30°终边相同的角中有几个角属于二、探究新知知识小结3:所有与角α终边相同的角,连同角α在内可构成一个集合
S={β|β=k·360°+α,k∈Z}
即任一与角α终边相同的角,都可以表示成α与整数个周角的和. 三、实践运用例1:在0°到360°范围内,分别找出与640°终边相同的角,并判定它们是第几象限。
当k=-1时我们得到角 280°,
所以与640°角终边相同的角是280°角,它是第四象限角;
解:与640°终边相同的角可以写成k·360°+640°第二象限第一象限第三象限典型例题合作探究课本上的例1:
在0到360度内找与已知角终边相同的角,方法是:用所给角除以3600 , 若所给角是正的,按通常的除法进行;所给角是负的,角度除以3600,商是负数,它的绝对值应比被除数为其相反数时相应的商大1,以便使余数为正值。例1 在0°~360°范围内,找出与-950°12′角终边相同的角并判定它是第几象限角: 解 : ∵-950°12′= 129048′-3×3600, ∴在0°~360°范围内, 与-950°12′角终边相同的角是129°48′, 它是第二象限角.例2 写出终边落在y轴上的角的集合。终边落在坐标轴上的情形0090018002700 + k?360° + k?360° + k?360° + k?360° 或3600+ k?360° 例2 写出终边落在y轴上的角的集合。解:在0°~360°范围内,在终边在y轴上的角有两个,90°,270°S1={β| β=900+K?3600,K∈Z} ={β| β=900+2K?1800,K∈Z}∴与270°角终边相同的角构成的集合S2={β| β=2700+K?3600,K∈Z}
={β| β=900+1800+2K?1800,K∈Z}
∪{β| β=900+(2K+1)1800 ,K∈Z}
S=S1∪S2所以 终边落在y轴上的角的集合为={β| β=900+K?1800 ,K∈Z}
{偶数}∪{奇数}={整数}∴与90°角终边相同的角构成的集合课堂小结:
终边在x轴正半轴上的角的集合:{?|?=k?360?, k?Z};
终边在x轴负半轴上的角的集合:{?|?=k?360?+180?,k?Z};
终边在x轴上的角的集合:{?|?=k?180?,k?Z};
终边在y轴正半轴上的角的集合:{?|?=k?360?+90?,k?Z};
终边在y轴负半轴上的角的集合:{?|?=k?360?+270?,k?Z};
终边在y轴上的角的集合:{?|?=k?180?+90?,k?Z};
终边在坐标轴上的角的集合:{?|?=k?90?,k?Z}.终边落在坐标轴上的情形0090018002700 + k?360° + k?360° + k?360° + k?360° 或3600+ k?360° 合作探究第一象限角的集合:
S={β/ 0o+K·360o< β < 90o+K·360o,K∈Z};
第二象限角的集合:
S={β/ 90o+K·360o< β < 180o+K·360o,K∈Z};
第三象限角的集合:
S={β/ 180o+K·360o< β < 270o+K·360o,K∈Z};第四象限角的集合:
S={β/ 270o+K·360o< β < 360o+K·360o,K∈Z};例4.如果 是第三象限角,那么2 角终边的位置如
何? 是哪个象限的角?解:利用上述方法判断,可得如下结论:12341234S={α|α=45°+k·180°,k∈Z}.-315°,-135°,45°,225°,405°,585°. 解: 例3 写出终边在直线y=x上的角的集合S,并把S中适合不等式-360°≤ <720°的元素写出来. 四、练习提高1.下列命题中正确的是
(A)第一象限角一定不是负角
(B)小于 的角一定是锐角
(C) 钝角一定是第二象限角
(D)第一象限角一定是锐角2.分针在1小时内所转过的角度是 ;时针转过的角度是 .
3.分别作出下列各角的终边,并指出它们
是第几象限角:4.下列各命题:
(1)相等的角终边一定相同;(2)终边相同的角一定相等;(3)第二象限的角一定大于第一象限任意一个角;(4)若 , 则 必是第一或第二象限角
其中正确的有 ( )练习例7C练习例11
