北师大版八年级数学上册 第三章位置与坐标 回顾与思考 优质课件(共13张PPT)
文档属性
| 名称 | 北师大版八年级数学上册 第三章位置与坐标 回顾与思考 优质课件(共13张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 971.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-07 00:00:00 | ||
图片预览




文档简介
(共13张PPT)
八年级数学上册
(北师大版)
第三章 位置与坐标
回顾与思考
百合塔
百花馆
玫瑰园
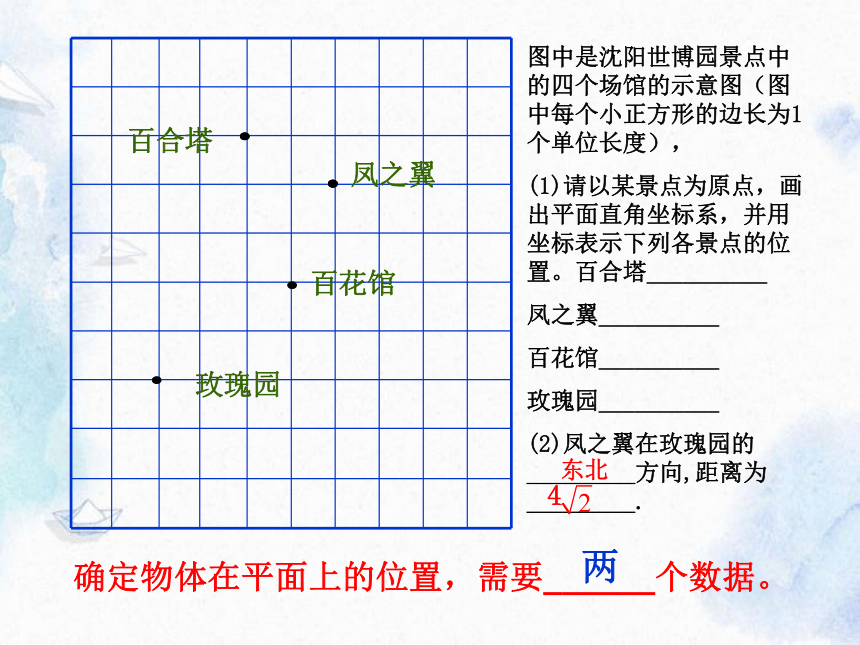
图中是沈阳世博园景点中的四个场馆的示意图(图中每个小正方形的边长为1个单位长度),
(1)请以某景点为原点,画出平面直角坐标系,并用坐标表示下列各景点的位置。百合塔__________
凤之翼__________
百花馆__________
玫瑰园__________
(2)凤之翼在玫瑰园的_________方向,距离为_________.
确定物体在平面上的位置,需要______个数据。
两
凤之翼
东北
4
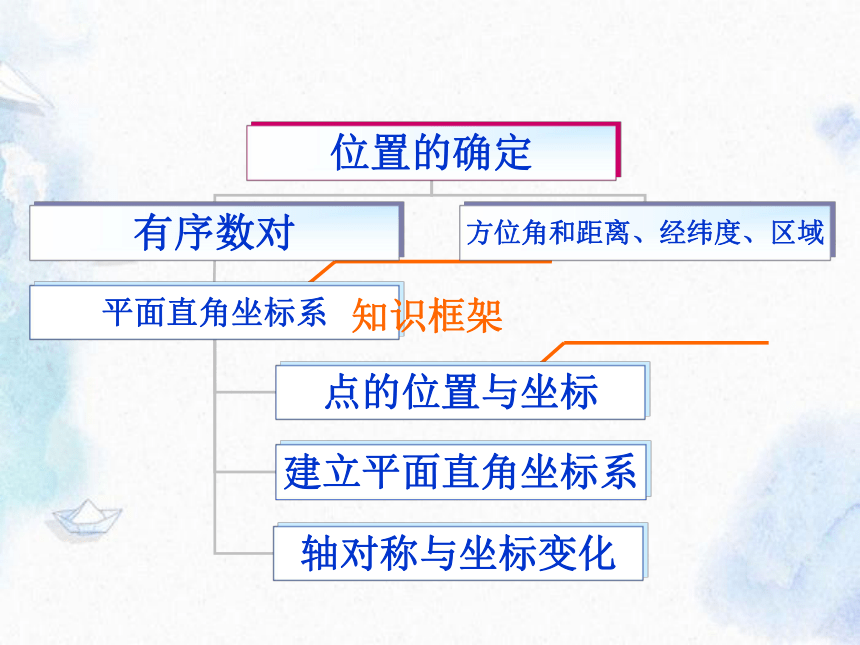
位置的确定
有序数对
方位角和距离、经纬度、区域
平面直角坐标系
点的位置与坐标
建立平面直角坐标系
轴对称与坐标变化
知识框架
1、点M(3a-1,1-5a)在y轴上,则M的坐标
为 。
2、点A(a-1,-3)在第四象限,点B(2,b-1)在第一象限,则点P(b,-a)的第 象限.
3、坐标平面上第二象限内有一点P到x轴的距离是4,到y轴的距离是5,则P点的坐标为_______。 4、已知点A(1,2),AB∥x轴,且AB=5,则B点坐标是___________________。
5、点P(a,b)与点Q(1,2)关于x轴对称,a+b=________。
练习一
(0,- )
四
(-5,4)
(6,2)或(-4,2)
-1
小结
1、x轴上点的坐标______,y轴上点的坐标______,
原点坐标_______.
象限内点坐标的符号特征:
第一象限_____,第二象限_____,第三象限_____,
第四象限_____.
2、点P(x,y)到x轴的距离为____,到y轴的距离为______。
3、平行于x轴的直线上的点的_____坐标_____,平行于y轴的直线上的点的_____坐标_____.
4、关于x轴对称的点____________________________;
关于y轴对称的点_____________________________;
关于原点对称的点____________________________.
(x,0)
(0,y)
(0,0)
纵
相同
横
相同
横坐标相等,纵坐标互为相反数
纵坐标相等,横坐标互为相反数
横纵坐标都互为相反数
(+,+)
(-,+)
(-,-)
(+,-)
∣y∣
∣x∣
练习二
1、点P(2–a, 3a+6),且点P到两轴的距离相
等,则点P的坐标为( )
A. (3, 3) B. (3, –3)
C、(6, -6) D. (3, 3)或(6, -6)
2、已知P点坐标(3,a),且点P到原点的距离为
5,则点P的坐标为__________________.
3、已知点A(0,2),B(4,1),点P是x轴上的一点,则PA+PB的最小值是 。
D
(3,4)或(3,-4)
5
小结
1、一三象限角平分线和二四象限角平分线上的
点到两坐标轴的距离相等,注意有时要考虑这两种情
况的存在.
一三象限角平分线上的点横、纵坐标同号;
二四象限角平分线上的点横、纵坐标异号,
2、P(x,y)到原点的距离为_________
3、直线同侧距离和最短的问题应利用轴对称,构造直角三角形,转化为勾股定理解决。
例2、△ABC三个顶点A、B、C的坐标分别为
A(2,-1)
B(1,-3)
C(4,-5)
(1)求△ABC的面积,
(2)求△ABC的三边长,判断三角形形状。
C
B
A
y
x
AB= ,AC=2 ,BC=
钝角三角形
1、在平面直角坐标系中放置了一个边长为 的正方形,如图所示,点B在y轴上,且坐标(0,2),点C在x轴上,则点D的坐标为__________。
(3,1)
E
练习三
练习三
y
x
C
O
B
A
D
o
1
1
o
1
1
o
1
x
y
o
1
o
A
B
P
C
1
o
1
o
1
o
1
o
2、如图所示,在平面直角坐标系中,一颗棋子从点P处开始依次关于点A,B,C作循环对称跳动,即第一次跳到点P关于点A的对称点M处,接着跳到点M关于点B的对称点N处,第三次跳到点N关于点C的对称点处,…,如此下去。
(1)在图画出点M,N,并写出点M,N的坐标;
(2)求经过第2017次跳动之后,棋子落点与点P的距离。
(1)M(-2,0),N(4,4)
(2)棋子跳动3次后又回到点P处,所以经过第2017次跳动后,棋子落在点M处,PM=2
M
N
关于平面直角坐标系你还学会了哪些?
回顾与思考
位置与坐标
例1、在直角坐标系中,标出下列各点的坐标:
(1)点A在x轴上,位于原点的左侧,距离坐标原点4个单位长度;
(2)点B在y轴上,位于原点的上方,距离坐标原点4个单位长度;
(3)点C在y轴左侧,在x轴上方,距离每个坐标轴都是4个单位长度。
(4)A、B、C三点构成什么图形,线段AC、BC、AB长分别是多少?
答:(4)等腰直角三角形
AC=4,BC=4
AB=4
O
A
C
B
O
A
C
B
O
A
C
B
O
A
C
B
O
A
C
B
O
A
C
B
O
A
C
B
O
A
C
B
O
A
C
B
O
A
C
B
O
A
C
B
O
A
C
B
O
A
C
B
x
y
八年级数学上册
(北师大版)
第三章 位置与坐标
回顾与思考
百合塔
百花馆
玫瑰园
图中是沈阳世博园景点中的四个场馆的示意图(图中每个小正方形的边长为1个单位长度),
(1)请以某景点为原点,画出平面直角坐标系,并用坐标表示下列各景点的位置。百合塔__________
凤之翼__________
百花馆__________
玫瑰园__________
(2)凤之翼在玫瑰园的_________方向,距离为_________.
确定物体在平面上的位置,需要______个数据。
两
凤之翼
东北
4
位置的确定
有序数对
方位角和距离、经纬度、区域
平面直角坐标系
点的位置与坐标
建立平面直角坐标系
轴对称与坐标变化
知识框架
1、点M(3a-1,1-5a)在y轴上,则M的坐标
为 。
2、点A(a-1,-3)在第四象限,点B(2,b-1)在第一象限,则点P(b,-a)的第 象限.
3、坐标平面上第二象限内有一点P到x轴的距离是4,到y轴的距离是5,则P点的坐标为_______。 4、已知点A(1,2),AB∥x轴,且AB=5,则B点坐标是___________________。
5、点P(a,b)与点Q(1,2)关于x轴对称,a+b=________。
练习一
(0,- )
四
(-5,4)
(6,2)或(-4,2)
-1
小结
1、x轴上点的坐标______,y轴上点的坐标______,
原点坐标_______.
象限内点坐标的符号特征:
第一象限_____,第二象限_____,第三象限_____,
第四象限_____.
2、点P(x,y)到x轴的距离为____,到y轴的距离为______。
3、平行于x轴的直线上的点的_____坐标_____,平行于y轴的直线上的点的_____坐标_____.
4、关于x轴对称的点____________________________;
关于y轴对称的点_____________________________;
关于原点对称的点____________________________.
(x,0)
(0,y)
(0,0)
纵
相同
横
相同
横坐标相等,纵坐标互为相反数
纵坐标相等,横坐标互为相反数
横纵坐标都互为相反数
(+,+)
(-,+)
(-,-)
(+,-)
∣y∣
∣x∣
练习二
1、点P(2–a, 3a+6),且点P到两轴的距离相
等,则点P的坐标为( )
A. (3, 3) B. (3, –3)
C、(6, -6) D. (3, 3)或(6, -6)
2、已知P点坐标(3,a),且点P到原点的距离为
5,则点P的坐标为__________________.
3、已知点A(0,2),B(4,1),点P是x轴上的一点,则PA+PB的最小值是 。
D
(3,4)或(3,-4)
5
小结
1、一三象限角平分线和二四象限角平分线上的
点到两坐标轴的距离相等,注意有时要考虑这两种情
况的存在.
一三象限角平分线上的点横、纵坐标同号;
二四象限角平分线上的点横、纵坐标异号,
2、P(x,y)到原点的距离为_________
3、直线同侧距离和最短的问题应利用轴对称,构造直角三角形,转化为勾股定理解决。
例2、△ABC三个顶点A、B、C的坐标分别为
A(2,-1)
B(1,-3)
C(4,-5)
(1)求△ABC的面积,
(2)求△ABC的三边长,判断三角形形状。
C
B
A
y
x
AB= ,AC=2 ,BC=
钝角三角形
1、在平面直角坐标系中放置了一个边长为 的正方形,如图所示,点B在y轴上,且坐标(0,2),点C在x轴上,则点D的坐标为__________。
(3,1)
E
练习三
练习三
y
x
C
O
B
A
D
o
1
1
o
1
1
o
1
x
y
o
1
o
A
B
P
C
1
o
1
o
1
o
1
o
2、如图所示,在平面直角坐标系中,一颗棋子从点P处开始依次关于点A,B,C作循环对称跳动,即第一次跳到点P关于点A的对称点M处,接着跳到点M关于点B的对称点N处,第三次跳到点N关于点C的对称点处,…,如此下去。
(1)在图画出点M,N,并写出点M,N的坐标;
(2)求经过第2017次跳动之后,棋子落点与点P的距离。
(1)M(-2,0),N(4,4)
(2)棋子跳动3次后又回到点P处,所以经过第2017次跳动后,棋子落在点M处,PM=2
M
N
关于平面直角坐标系你还学会了哪些?
回顾与思考
位置与坐标
例1、在直角坐标系中,标出下列各点的坐标:
(1)点A在x轴上,位于原点的左侧,距离坐标原点4个单位长度;
(2)点B在y轴上,位于原点的上方,距离坐标原点4个单位长度;
(3)点C在y轴左侧,在x轴上方,距离每个坐标轴都是4个单位长度。
(4)A、B、C三点构成什么图形,线段AC、BC、AB长分别是多少?
答:(4)等腰直角三角形
AC=4,BC=4
AB=4
O
A
C
B
O
A
C
B
O
A
C
B
O
A
C
B
O
A
C
B
O
A
C
B
O
A
C
B
O
A
C
B
O
A
C
B
O
A
C
B
O
A
C
B
O
A
C
B
O
A
C
B
x
y
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
