第五单元_第12课时_实际问题与方程(三)(教学课件)-五年级数学上册人教版 (共26张PPT)
文档属性
| 名称 | 第五单元_第12课时_实际问题与方程(三)(教学课件)-五年级数学上册人教版 (共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-07 07:37:40 | ||
图片预览






文档简介
(共26张PPT)
第12课时_实际问题与方程(3)
小学数学·五年级(上)·RJ
目录
01
情境导入—引“探究”
知识链接—构“联系”
02
新知探究—习“方法”
03
05
作业布置---拓“延伸”
达标练习---活“应用”
04
1.会分析实际问题中数量间的相等关系,能根据题中的数量关系列形如a(x±b)=c的方程来解决问题。
2.掌握列方程解决实际问题的一般步骤,体会用方程解决实际问题的优越性。
3.感受数学与实际的紧密联系,初步建立方程意识、建模思想,促进抽象思维的发展和提升。
会分析实际问题中数量间的相等关系,能根据题中的数量关系列形如a(x±b)=c的方程来解决问题。
掌握列方程解决实际问题的步骤,体会用方程解决实际问题的优越性。
利用迁移类推的方法去解决实际问题的过程,培养方程意识和解决问题的策略方法。
重 点
核心素养
难 点
课前引入
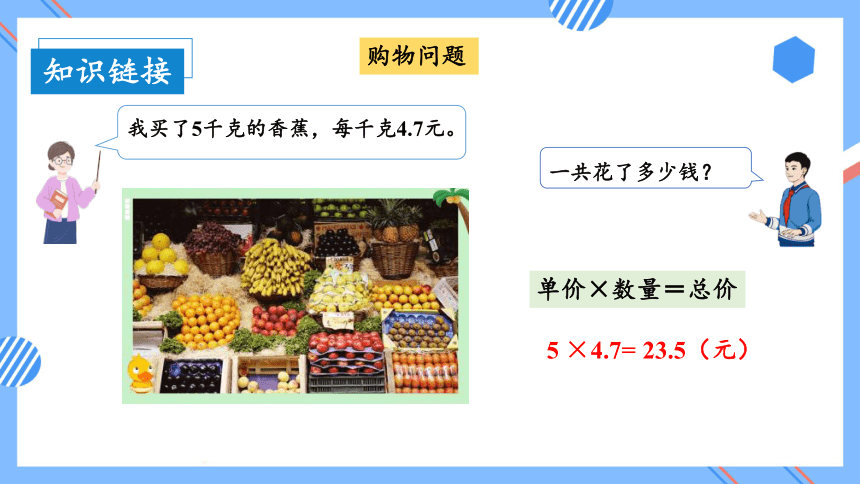
在购物时我们要想知道花了多少钱?需要知道购买物品的数量和单价。
购物问题
在购物问题中,单价x数量=总价,下次购物时我们可以检验花费的钱数是否正确。
阅读题目,寻找信息,分析实际问题中的等量关系。
购物问题
单价×数量=总价
5 ×4.7= 23.5(元)
我买了5千克的香蕉,每千克4.7元。
一共花了多少钱?
探究:形如a(x±b)=c的方程的解法?它的理论依据又是什么?
你能用不同的方法解下面两个方程吗?
(1) 2(x-16)=8
解: 2x-32=8
2x-32+32=8 +32
2x=40
x=20
(2)2(6x+3)=600
解: (6x+3)÷2=600÷2
6x+3=300
6x=297
x=49.5
想一想,说一说:形如a(x±b)=c的方程的解法吗?
归纳总结:
形如a(x±b)=c的方程有两种解法:
1.把小括号里的x±b看作一个整体,先求出x±b的值,再求出x的值。
2.根据乘法分配律,把a(x±b)=c转化成ax±ab=c的方程,求出ax的值,再求出x的值。
读题,你获取了哪些数学信息?
妈妈买苹果和梨各2kg,共花费16.4元。梨每千克3.8元,苹果每千克多少钱?
妈妈买苹果和梨各2kg,共花费16.4元。梨每千克3.8元,苹果每千克多少钱?
数学问题
总价
梨的单价
要解决的问题是:求苹果的单价。
注意:“各2 kg”是什么意思?
阅读与理解
能根据题中的数量关系列形如a(x±b)=c的方程来解决问题。
妈妈买苹果和梨各2kg,共花费16.4元。梨每千克3.8元,苹果每千克多少钱?
要解决的问题是:求苹果的单价。
苹果的总价+梨的总价=总价钱
答:苹果每千克4.4元。
方法一:
2x=8.8
x=4.4
2x÷2=8.8÷2
2x+7.6-7.6=16.4-7.6
2x+7.6=16.4
2x+3.8×2=16.4
分析与解答
妈妈买苹果和梨各2kg,共花费16.4元。梨每千克3.8元,苹果每千克多少钱?
分析与解答
两种水果的单价总和×2=总价钱
答:苹果每千克4.4元。
方法二:
(3.8+x)×2=16.4
x=4.4
3.8+x=8.2
(3.8+x)×2 ÷2=16.4÷2
3.8+x-3.8=8.2-3.8
把什么看成一个整体?
把3.8+x看作一个整体
2x + 2.8×2 = 10.4
2x + 5.6 = 10.4
2x + 5.6 – 5.6 = 10.4 – 5.6
2x = 4.8
2x÷2 = 4.8÷2
x = 2.4
(2.8 +x)×2 = 10.4
(2.8 +x)×2 ÷2 = 10.4÷2
2.8 + x = 5.2
2.8 + x – 2.8 = 5.2 – 2.8
x = 2.4
乘法分配律
这两个方程之间有什么联系吗?
怎样检验这道题是否正确?
回顾与反思
2x + 2.8×2 = 10.4
2x + 5.6 = 10.4
2x + 5.6 – 5.6 = 10.4 – 5.6
2x = 4.8
2x÷2 = 4.8÷2
x = 2.4
(2.8 +x)×2 = 10.4
(2.8 +x)×2 ÷2 = 10.4÷2
2.8 + x = 5.2
2.8 + x – 2.8 = 5.2 – 2.8
x = 2.4
乘法分配律
回顾与反思
苹果的总价 + 梨的总价 = 总钱数
两种水果的单价总和×2 = 总钱数
2×2.4 +2.8×2 =10.4 =总价钱
(2.8 +2.4)×2 =10.4 =总价钱
检验:
归纳总结:
1.根据乘法分配律,可以把形如ax±ab=c的方程
转化为形如a(x±b)=c的方程。
2.解形如ax±ab=c的方程时,把ax看成一个整体,先
算ax的值,再求出x的值。
3.解形如a(x±b)=c的方程时,把(x±b)看成一个整体,
先求出(x±b)的值,再求出x的值。
掌握列方程解决实际问题的步骤,体会用方程解决实际问题的优越性。
2( x-2.6 )=8 5( x+1.5 )=17.5
8( x-6.2 )=41.6 ( x-3 )÷2=7.5
课堂练习
1.解下列方程。
解: x-2.6=4
x=6.6
解: x+1.5=3.5
x=2
解: x-6.2=5.2
x=11.4
解: x-3=15
x=18
课堂练习
2.爸爸、妈妈带小明、小丽去公园游玩,买了4张门票共花了11元,其中成人票每张4元,儿童票每张多少钱?
解:设儿童票每张x元。
(4+x)×2=11
x=1.5
答:儿童票每张1.5元。
学以致用
3.小明收集了一些易拉罐和塑料瓶,卖到废品回收站,每个都是0.12元,一共卖了1.8元。其中易拉罐有6个,塑料瓶有几个?
解:设塑料瓶有x个。
(6+x)×0.12=1.8
(6+x)×0.12÷0.12=1.8÷0.12
6+x=15
x=9
答:塑料瓶有9个。
学以致用
4.小红买两套丛书一共花了92元。“科学家”丛书12.5元/本,“发明家”丛书14元/本。其中“科学家”丛书有4本,“发明家”丛书有多少本?
解:设“发明家”丛书有x本。
12.5×4+14x=92
50+14x=92
14x=42
x=3
答:“发明家”丛书有3本。
拓展提升
5.请算出每个盘子多少钱?
产品 数量 单价 金额/元
碗 4 5.8元 23.2
盘子 4 12.7元 50.8
总计金额 74
4×5.8+4x = 74
x =12.7
答:每个盘子12.7元。
解:设每个盘子x元。
拓展提升
6.(易错题)小梦今年8岁,再过五年,爷爷的年龄刚好是小梦的5倍,爷爷今年多少岁?
解:设爷爷今年x岁。
答:爷爷今年60岁。
(x+5)÷5=8+5
x=60
这节课你有什么收获?
1.把小括号里的x±b看作一个整体,先求出x±b的值,再求出x的值。
2.根据乘法分配律,把a(x±b)=c转化成ax±ab=c的方程,求出ax的
值,再求出x的值。
形如a(x±b)=c的方程有两种解法:
实际问题与方程(三):
1.把要求的未知数设成x,再列方程;
2.求出的解的后面不写单位名称;
3.检验作答。
第12课时_实际问题与方程(3)
小学数学·五年级(上)·RJ
目录
01
情境导入—引“探究”
知识链接—构“联系”
02
新知探究—习“方法”
03
05
作业布置---拓“延伸”
达标练习---活“应用”
04
1.会分析实际问题中数量间的相等关系,能根据题中的数量关系列形如a(x±b)=c的方程来解决问题。
2.掌握列方程解决实际问题的一般步骤,体会用方程解决实际问题的优越性。
3.感受数学与实际的紧密联系,初步建立方程意识、建模思想,促进抽象思维的发展和提升。
会分析实际问题中数量间的相等关系,能根据题中的数量关系列形如a(x±b)=c的方程来解决问题。
掌握列方程解决实际问题的步骤,体会用方程解决实际问题的优越性。
利用迁移类推的方法去解决实际问题的过程,培养方程意识和解决问题的策略方法。
重 点
核心素养
难 点
课前引入
在购物时我们要想知道花了多少钱?需要知道购买物品的数量和单价。
购物问题
在购物问题中,单价x数量=总价,下次购物时我们可以检验花费的钱数是否正确。
阅读题目,寻找信息,分析实际问题中的等量关系。
购物问题
单价×数量=总价
5 ×4.7= 23.5(元)
我买了5千克的香蕉,每千克4.7元。
一共花了多少钱?
探究:形如a(x±b)=c的方程的解法?它的理论依据又是什么?
你能用不同的方法解下面两个方程吗?
(1) 2(x-16)=8
解: 2x-32=8
2x-32+32=8 +32
2x=40
x=20
(2)2(6x+3)=600
解: (6x+3)÷2=600÷2
6x+3=300
6x=297
x=49.5
想一想,说一说:形如a(x±b)=c的方程的解法吗?
归纳总结:
形如a(x±b)=c的方程有两种解法:
1.把小括号里的x±b看作一个整体,先求出x±b的值,再求出x的值。
2.根据乘法分配律,把a(x±b)=c转化成ax±ab=c的方程,求出ax的值,再求出x的值。
读题,你获取了哪些数学信息?
妈妈买苹果和梨各2kg,共花费16.4元。梨每千克3.8元,苹果每千克多少钱?
妈妈买苹果和梨各2kg,共花费16.4元。梨每千克3.8元,苹果每千克多少钱?
数学问题
总价
梨的单价
要解决的问题是:求苹果的单价。
注意:“各2 kg”是什么意思?
阅读与理解
能根据题中的数量关系列形如a(x±b)=c的方程来解决问题。
妈妈买苹果和梨各2kg,共花费16.4元。梨每千克3.8元,苹果每千克多少钱?
要解决的问题是:求苹果的单价。
苹果的总价+梨的总价=总价钱
答:苹果每千克4.4元。
方法一:
2x=8.8
x=4.4
2x÷2=8.8÷2
2x+7.6-7.6=16.4-7.6
2x+7.6=16.4
2x+3.8×2=16.4
分析与解答
妈妈买苹果和梨各2kg,共花费16.4元。梨每千克3.8元,苹果每千克多少钱?
分析与解答
两种水果的单价总和×2=总价钱
答:苹果每千克4.4元。
方法二:
(3.8+x)×2=16.4
x=4.4
3.8+x=8.2
(3.8+x)×2 ÷2=16.4÷2
3.8+x-3.8=8.2-3.8
把什么看成一个整体?
把3.8+x看作一个整体
2x + 2.8×2 = 10.4
2x + 5.6 = 10.4
2x + 5.6 – 5.6 = 10.4 – 5.6
2x = 4.8
2x÷2 = 4.8÷2
x = 2.4
(2.8 +x)×2 = 10.4
(2.8 +x)×2 ÷2 = 10.4÷2
2.8 + x = 5.2
2.8 + x – 2.8 = 5.2 – 2.8
x = 2.4
乘法分配律
这两个方程之间有什么联系吗?
怎样检验这道题是否正确?
回顾与反思
2x + 2.8×2 = 10.4
2x + 5.6 = 10.4
2x + 5.6 – 5.6 = 10.4 – 5.6
2x = 4.8
2x÷2 = 4.8÷2
x = 2.4
(2.8 +x)×2 = 10.4
(2.8 +x)×2 ÷2 = 10.4÷2
2.8 + x = 5.2
2.8 + x – 2.8 = 5.2 – 2.8
x = 2.4
乘法分配律
回顾与反思
苹果的总价 + 梨的总价 = 总钱数
两种水果的单价总和×2 = 总钱数
2×2.4 +2.8×2 =10.4 =总价钱
(2.8 +2.4)×2 =10.4 =总价钱
检验:
归纳总结:
1.根据乘法分配律,可以把形如ax±ab=c的方程
转化为形如a(x±b)=c的方程。
2.解形如ax±ab=c的方程时,把ax看成一个整体,先
算ax的值,再求出x的值。
3.解形如a(x±b)=c的方程时,把(x±b)看成一个整体,
先求出(x±b)的值,再求出x的值。
掌握列方程解决实际问题的步骤,体会用方程解决实际问题的优越性。
2( x-2.6 )=8 5( x+1.5 )=17.5
8( x-6.2 )=41.6 ( x-3 )÷2=7.5
课堂练习
1.解下列方程。
解: x-2.6=4
x=6.6
解: x+1.5=3.5
x=2
解: x-6.2=5.2
x=11.4
解: x-3=15
x=18
课堂练习
2.爸爸、妈妈带小明、小丽去公园游玩,买了4张门票共花了11元,其中成人票每张4元,儿童票每张多少钱?
解:设儿童票每张x元。
(4+x)×2=11
x=1.5
答:儿童票每张1.5元。
学以致用
3.小明收集了一些易拉罐和塑料瓶,卖到废品回收站,每个都是0.12元,一共卖了1.8元。其中易拉罐有6个,塑料瓶有几个?
解:设塑料瓶有x个。
(6+x)×0.12=1.8
(6+x)×0.12÷0.12=1.8÷0.12
6+x=15
x=9
答:塑料瓶有9个。
学以致用
4.小红买两套丛书一共花了92元。“科学家”丛书12.5元/本,“发明家”丛书14元/本。其中“科学家”丛书有4本,“发明家”丛书有多少本?
解:设“发明家”丛书有x本。
12.5×4+14x=92
50+14x=92
14x=42
x=3
答:“发明家”丛书有3本。
拓展提升
5.请算出每个盘子多少钱?
产品 数量 单价 金额/元
碗 4 5.8元 23.2
盘子 4 12.7元 50.8
总计金额 74
4×5.8+4x = 74
x =12.7
答:每个盘子12.7元。
解:设每个盘子x元。
拓展提升
6.(易错题)小梦今年8岁,再过五年,爷爷的年龄刚好是小梦的5倍,爷爷今年多少岁?
解:设爷爷今年x岁。
答:爷爷今年60岁。
(x+5)÷5=8+5
x=60
这节课你有什么收获?
1.把小括号里的x±b看作一个整体,先求出x±b的值,再求出x的值。
2.根据乘法分配律,把a(x±b)=c转化成ax±ab=c的方程,求出ax的
值,再求出x的值。
形如a(x±b)=c的方程有两种解法:
实际问题与方程(三):
1.把要求的未知数设成x,再列方程;
2.求出的解的后面不写单位名称;
3.检验作答。
