直线和圆的位置关系[上学期]
文档属性
| 名称 | 直线和圆的位置关系[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 17.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-10-19 16:42:00 | ||
图片预览

文档简介
直线和圆的位置关系学案
设计:黄亚军 审核:许滨
班级 姓名 学号
一、学习目标
1.知识目标:能说出直线和圆的三种位置关系的定义;掌握直线和圆的位置关系的性质和判定,会根据给出的条件确定直线和圆的位置关系.
2.能力目标:会用运动的观点研究直线和圆的位置关系,培养运动变化的辩证唯物主义观点;培养自己通过实践来探索、总结、归纳数学规律的能力.
3.情感目标:培养自己合作学习的能力,激发自己的学习兴趣.
二、学习过程
活动1感知直线和圆的位置关系
1. 感知屏幕下沿在下降过程中与圆的位置关系;
2. 感知太阳在升起过程中相对于地平线的位置变化情况.
活动2从“形”的角度判定直线和圆的位置关系
1.在纸上画一条直线,把钥匙环看作一个圆,在纸上移动钥匙环,观察钥匙环移动的过程,通过观察,进行思考:能否把圆相对于直线的运动过程分成若干种情况?如果能,把下面的画图区上下分隔成若干块,画出直线和圆的不同位置情形.
直线和圆的位置关系 画图区 直线名称
2.由定义,直线和圆的位置关系可以由 判定.
若直线和圆 公共点,则这条直线和圆相交;
若直线和圆 公共点,则这条直线和圆相切;
若直线和圆 公共点,则这条直线和圆相离.
〔反馈练习〕
1.判断下列说法是否正确.
(1)直线与圆最多有两个公共点;( )
(2)若A是⊙O上一点, 则直线AB与⊙O相切;( )
(3)若A、B是⊙O外两点, 则直线AB与⊙O相离.( )
2.若直线l与⊙O的公共点的个数不少于1个,则直线l与⊙O的位置关系
是 .
3.若C为⊙O外一点,则过点C的直线CD与⊙O的位置关系是 .
请通过画图加以说明:
第1题(1) 第1题(2) 第1题(3)
第2题 第3题
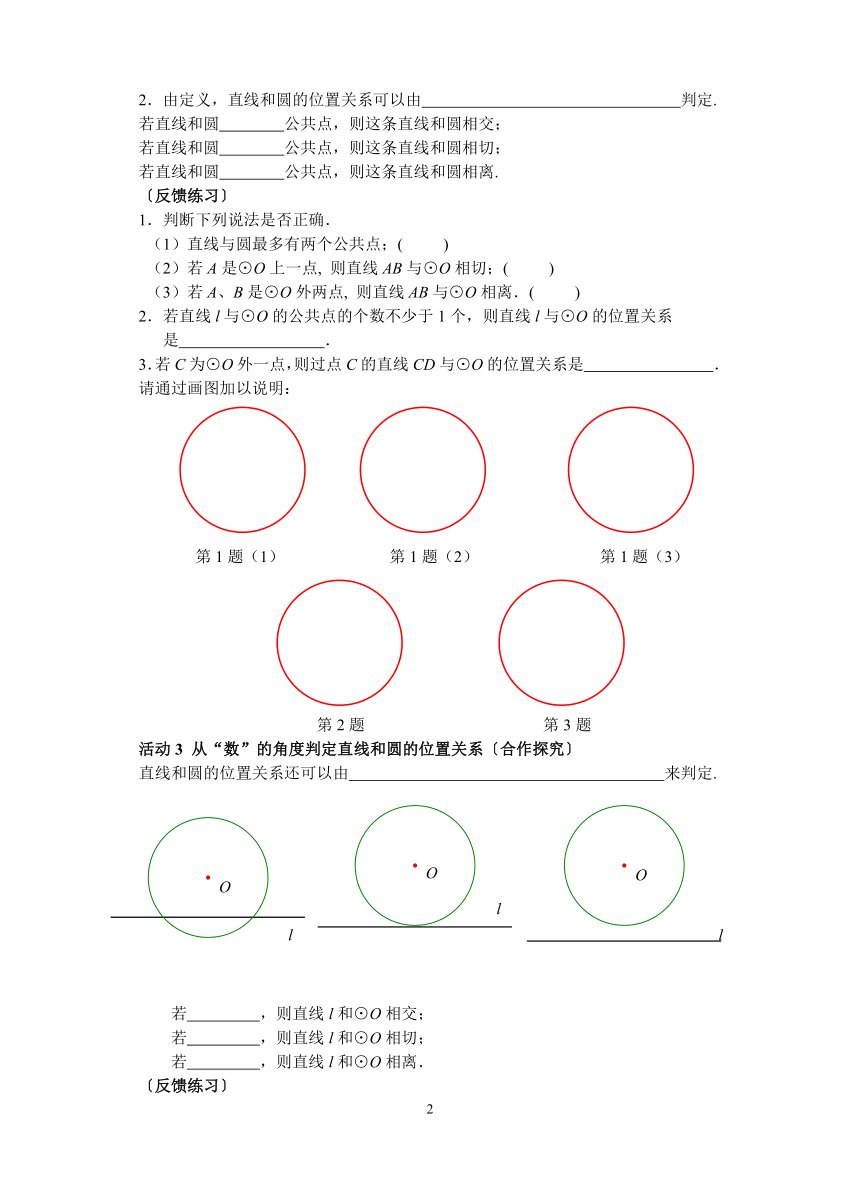
活动3 从“数”的角度判定直线和圆的位置关系〔合作探究〕
直线和圆的位置关系还可以由 来判定.
若 ,则直线l和⊙O相交;
若 ,则直线l和⊙O相切;
若 ,则直线l和⊙O相离.
〔反馈练习〕
1.已知圆的直径为13cm,设圆心到直线的距离为d.
(1)若d=4.5cm ,则直线和圆 ,直线和圆有____个公共点.
(2)若d=6.5cm ,则直线和圆______,直线和圆有____个公共点.
(3)若d=8 cm,则直线和圆______, 直线和圆有____个公共点.
2.已知⊙O的半径为5cm,圆心O与直线AB的距离为d,根据条件填写d的范围.
(1)若AB和⊙O相离,则 ;
(2)若AB和⊙O相切,则 ;
(3)若AB和⊙O相交,则 .
活动4 判定直线和圆的位置关系的方法归纳
判定直线与圆的位置关系的方法有两种:
(1) ;
(2) .
活动5 实际应用
例.在Rt△ABC中,C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径的
圆与直线AB有怎样的位置关系?为什么?
(1)r=2cm; (2)r=2.4cm; (3)r=3cm.
〔激活思维〕
若半径r为3.5cm,⊙C与直线AB的位置关系是 .
思考1:若半径r为3.5cm,⊙C与斜边AB的公共点的个数为 .
思考2:若⊙C与斜边AB只有一个公共点,则r的取值范围是 .
思考3:若⊙C与斜边AB没有公共点,则r的取值范围是 .
〔反馈练习〕
如图,已知∠AOB=30°,M为OB上一点,且OM=5cm,以M为圆心,r为半径的圆与直线OA有怎样的位置关系?为什么?
(1)r=2cm; (2)r=4cm; (3)r=2.5cm.
活动6 归纳小结
学后感
.
三、巩固练习
1.课本第102页练习第1题.
2.课本第110页练习第2题.
3.已知⊙O的直径为5cm,圆心O到直线l的距离为d.
(1)若d=2.5cm,则l与⊙O有 个公共点,此时l与⊙O的位置关系是 ;(2)若d=3cm,则l与⊙O有 个公共点,此时l与⊙O的位置关系是 ;
(3)若d=cm,则l与⊙O有 个公共点,此时l与⊙O的位置系
是 .
4.已知⊙O的半径r=4cm,弦AB=cm,则以点O为圆心,2cm长为半径的
圆与弦AB的位置关系是 .
5.在△ABC中,∠B=90°,AC=10,AB=5.
(1)以点A为圆心,分别以3、5、7为半径作圆,则这三个圆与BC边所在直线分别是什么位置关系?
(2)若以点C为圆心,则应以多长为半径作圆,才能与AB相切?
B
C
A
A
C
B
O
O
O
l
l
l
2
设计:黄亚军 审核:许滨
班级 姓名 学号
一、学习目标
1.知识目标:能说出直线和圆的三种位置关系的定义;掌握直线和圆的位置关系的性质和判定,会根据给出的条件确定直线和圆的位置关系.
2.能力目标:会用运动的观点研究直线和圆的位置关系,培养运动变化的辩证唯物主义观点;培养自己通过实践来探索、总结、归纳数学规律的能力.
3.情感目标:培养自己合作学习的能力,激发自己的学习兴趣.
二、学习过程
活动1感知直线和圆的位置关系
1. 感知屏幕下沿在下降过程中与圆的位置关系;
2. 感知太阳在升起过程中相对于地平线的位置变化情况.
活动2从“形”的角度判定直线和圆的位置关系
1.在纸上画一条直线,把钥匙环看作一个圆,在纸上移动钥匙环,观察钥匙环移动的过程,通过观察,进行思考:能否把圆相对于直线的运动过程分成若干种情况?如果能,把下面的画图区上下分隔成若干块,画出直线和圆的不同位置情形.
直线和圆的位置关系 画图区 直线名称
2.由定义,直线和圆的位置关系可以由 判定.
若直线和圆 公共点,则这条直线和圆相交;
若直线和圆 公共点,则这条直线和圆相切;
若直线和圆 公共点,则这条直线和圆相离.
〔反馈练习〕
1.判断下列说法是否正确.
(1)直线与圆最多有两个公共点;( )
(2)若A是⊙O上一点, 则直线AB与⊙O相切;( )
(3)若A、B是⊙O外两点, 则直线AB与⊙O相离.( )
2.若直线l与⊙O的公共点的个数不少于1个,则直线l与⊙O的位置关系
是 .
3.若C为⊙O外一点,则过点C的直线CD与⊙O的位置关系是 .
请通过画图加以说明:
第1题(1) 第1题(2) 第1题(3)
第2题 第3题
活动3 从“数”的角度判定直线和圆的位置关系〔合作探究〕
直线和圆的位置关系还可以由 来判定.
若 ,则直线l和⊙O相交;
若 ,则直线l和⊙O相切;
若 ,则直线l和⊙O相离.
〔反馈练习〕
1.已知圆的直径为13cm,设圆心到直线的距离为d.
(1)若d=4.5cm ,则直线和圆 ,直线和圆有____个公共点.
(2)若d=6.5cm ,则直线和圆______,直线和圆有____个公共点.
(3)若d=8 cm,则直线和圆______, 直线和圆有____个公共点.
2.已知⊙O的半径为5cm,圆心O与直线AB的距离为d,根据条件填写d的范围.
(1)若AB和⊙O相离,则 ;
(2)若AB和⊙O相切,则 ;
(3)若AB和⊙O相交,则 .
活动4 判定直线和圆的位置关系的方法归纳
判定直线与圆的位置关系的方法有两种:
(1) ;
(2) .
活动5 实际应用
例.在Rt△ABC中,C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径的
圆与直线AB有怎样的位置关系?为什么?
(1)r=2cm; (2)r=2.4cm; (3)r=3cm.
〔激活思维〕
若半径r为3.5cm,⊙C与直线AB的位置关系是 .
思考1:若半径r为3.5cm,⊙C与斜边AB的公共点的个数为 .
思考2:若⊙C与斜边AB只有一个公共点,则r的取值范围是 .
思考3:若⊙C与斜边AB没有公共点,则r的取值范围是 .
〔反馈练习〕
如图,已知∠AOB=30°,M为OB上一点,且OM=5cm,以M为圆心,r为半径的圆与直线OA有怎样的位置关系?为什么?
(1)r=2cm; (2)r=4cm; (3)r=2.5cm.
活动6 归纳小结
学后感
.
三、巩固练习
1.课本第102页练习第1题.
2.课本第110页练习第2题.
3.已知⊙O的直径为5cm,圆心O到直线l的距离为d.
(1)若d=2.5cm,则l与⊙O有 个公共点,此时l与⊙O的位置关系是 ;(2)若d=3cm,则l与⊙O有 个公共点,此时l与⊙O的位置关系是 ;
(3)若d=cm,则l与⊙O有 个公共点,此时l与⊙O的位置系
是 .
4.已知⊙O的半径r=4cm,弦AB=cm,则以点O为圆心,2cm长为半径的
圆与弦AB的位置关系是 .
5.在△ABC中,∠B=90°,AC=10,AB=5.
(1)以点A为圆心,分别以3、5、7为半径作圆,则这三个圆与BC边所在直线分别是什么位置关系?
(2)若以点C为圆心,则应以多长为半径作圆,才能与AB相切?
B
C
A
A
C
B
O
O
O
l
l
l
2
同课章节目录
