冀教版数学八年级上册13.4 三角形的尺规作图课件 (共22张PPT)
文档属性
| 名称 | 冀教版数学八年级上册13.4 三角形的尺规作图课件 (共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 154.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-07 08:20:35 | ||
图片预览





文档简介
(共22张PPT)
三角形的尺规作图
豆豆书上的三角形被墨迹污染了一部分,你能帮他在作业本上画出一个与书上完全一样的三角形吗?
如何作一个三角形与已有的三角形一样呢?
情境思考
思 考
只用直尺(没有刻度)和圆规也可以画出一些图形。这种方法被称为尺规作图.
用直尺(没有刻度)和圆规作图,是一种具有特殊要求的作图方法,这种作图方法不必用具体数据,只是按给定图形进行作图,这也是它与画图的区别所在.
学习新知
画图一般不限定工具,既可以用直尺和圆规,也可以用其他辅助工具,比如量角器、三角板、刻度尺等。在尺规作图中,直尺的作用只能用来连接两点之间的线段或过两点画直线和射线.
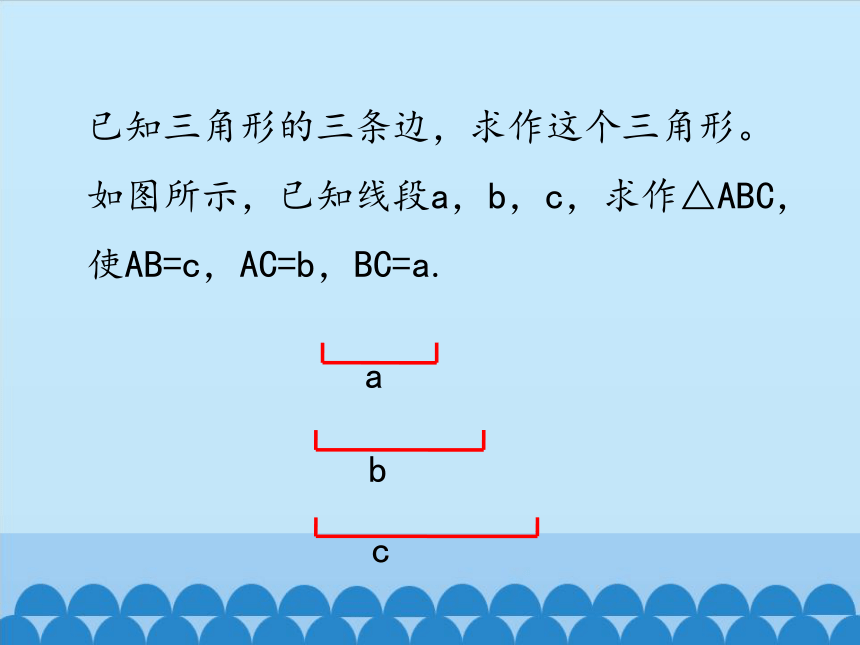
已知三角形的三条边,求作这个三角形。
如图所示,已知线段a,b,c,求作△ABC,使AB=c,AC=b,BC=a.
b
a
c
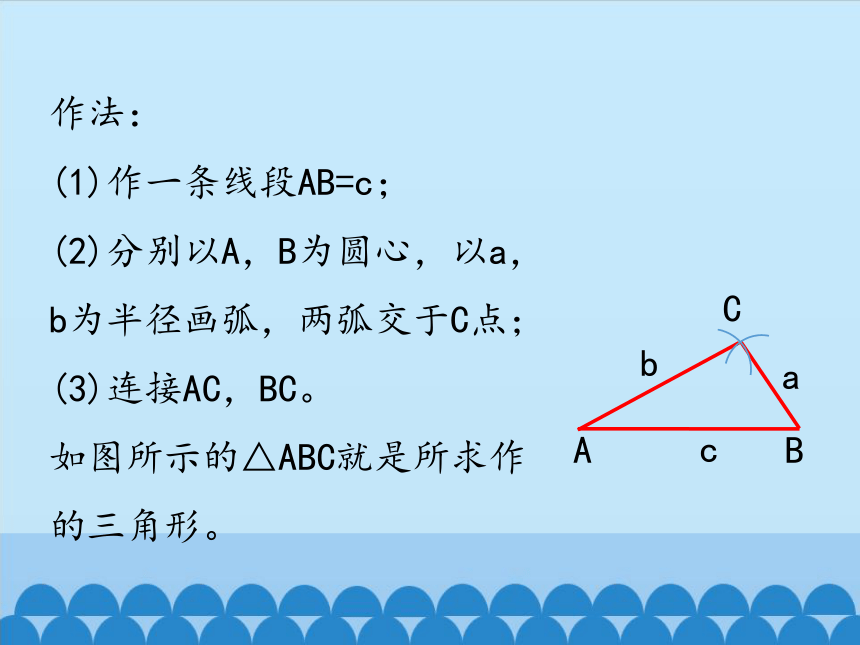
作法:
(1)作一条线段AB=c;
(2)分别以A,B为圆心,以a,b为半径画弧,两弧交于C点;
(3)连接AC,BC。
如图所示的△ABC就是所求作的三角形。
b
a
c
C
A
B
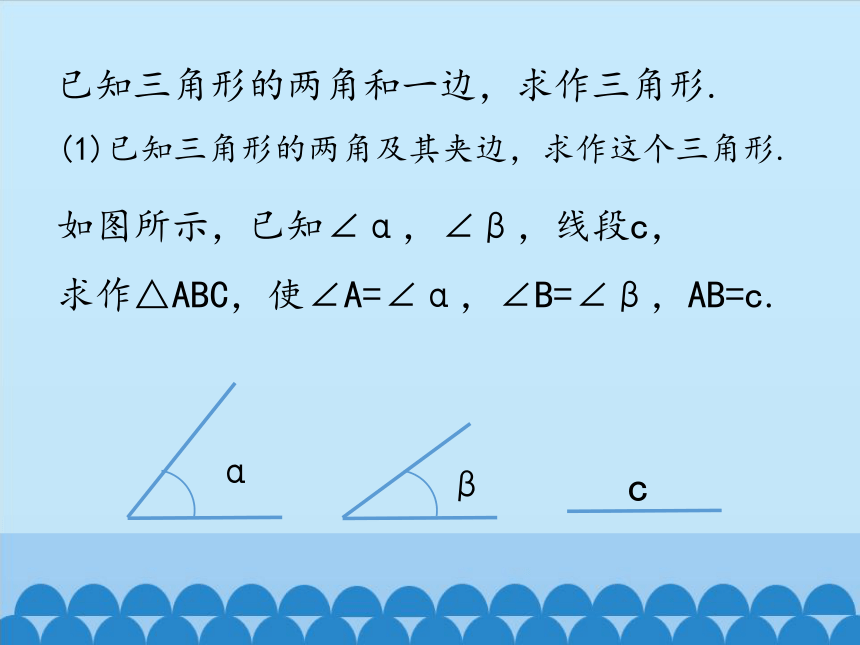
如图所示,已知∠α,∠β,线段c,
求作△ABC,使∠A=∠α,∠B=∠β,AB=c.
α
β
已知三角形的两角和一边,求作三角形.
(1)已知三角形的两角及其夹边,求作这个三角形.
c
作法:(1)作∠DAF=∠α;(2)在射线AF上截取线段AB=c;(3)以B为顶点,以BA为一边,作∠ABE=∠β,BE交AD于点C.则△ABC就是所求作的三角形.
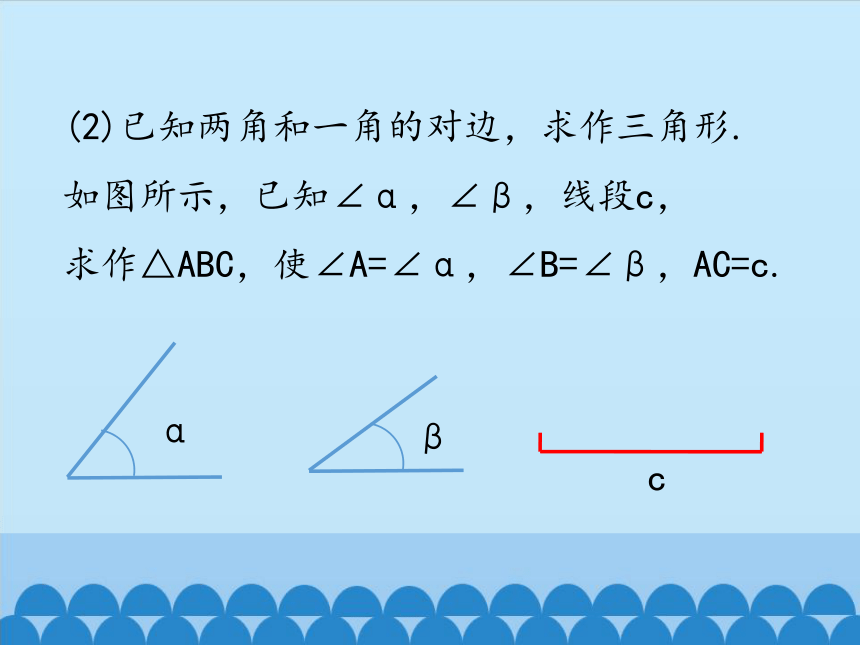
(2)已知两角和一角的对边,求作三角形.
如图所示,已知∠α,∠β,线段c,
求作△ABC,使∠A=∠α,∠B=∠β,AC=c.
β
c
α
先作出一个角等于∠α+∠β,通过反向延长角的一边得到它的补角,即三角形中的第三个内角∠γ。由此转换成已知∠α和∠γ及其这两角的夹边c,求作这个三角形.
已知三角形的两边和一角,求作三角形.
已知三角形的两边及夹角,求作这个三角形.
如图所示,已知线段a,b,∠α,
求作:△ABC,使BC=a,AB=b,∠ABC=∠α.
作法:(1)作∠DBE=∠α,(2)在射线BD,BE上分别截取BA=b,BC=a,(3)连接AC,△ABC就是所求作的三角形.
【规律方法小结】要掌握尺规作图的具体操作方法,按作图要求写作法时,要注意语言的规范性.
(1)用直尺作图时的规范性语言:
①过点 作直线 ,作线段 ,以点 为端点作射线 .②连接 ,以点 为端点作线段 ,延长线段 到点 ,使 = .
(2)用圆规作图时的规范性语言:
①以点 为圆心, 为半径作弧。②以点 为圆心, 为半径作弧,交 于点 .
课堂小结
1.作三角形的方法
作一个三角形与已知三角形全等,根据的就是三角形全等的条件。因此,作三角形时,所给的条件可以是三条边或两条边及夹角或两角及夹边或两角及一角的对边.
2.作三角形的步骤
在寻找作法的时候,一定要根据已知画出草图,确定作图步骤.
3.尺规作图的基本要求
①画图形;②写作法;③保留痕迹.
有些作图题,只要求保留痕迹,不用写作法.
检测反馈
1.尺规作图的画图工具是 ( )
A.刻度尺、量角器
B.三角板、量角器
C.直尺、量角器
D.没有刻度的直尺和圆规
D
解析:尺规作图的画图工具是没有刻度的直尺和圆规.故选D.
2.利用尺规作图,在下列条件中不能作出唯一直角三角形的是( )
A.已知两个锐角
B.已知一直角边和这边的对角
C.已知两条直角边
D.已知一个锐角和斜边
A
解析:A.因为已知两个锐角,而边长不确定,所以这样的三角形可作很多,而不是唯一的;B.符合全等三角形的判定“AAS”,能作出唯一直角三角形;C.符合全等三角形的判定“SAS”,能作出唯一直角三角形;D.符合全等三角形的判定“AAS”,能作出唯一直角三角形.故选A.
3.如图所示,△ABC是不等边三角形,DE=BC,以D,E为两个顶点作位置不同的三角形,使所作三角形与△ABC全等,这样的三角形最多可以作出( )
A.2个 B.4个 C.6个 D.8个
B
A
C
B
D
E
解析:可以作4个,分别是以D为圆心,AB长为半径作圆,以E为圆心,AC长为半径作圆.两圆相交于两点(DE上、下各一个),经过连接后可得到2个.然后以D为圆心,AC长为半径作圆,以E为圆心,AB长为半径作圆.两圆相交于两点(DE上、下各1个),经过连接后可得到2个.故选B.
4. 如图所示,已知线段a,用尺规作出△ABC,使AB=a,BC=AC=2a.
作法:
(1)先作一条线段等于2a,
(2)再作一条线段AB= ;
(3)分别以 、 为圆心,以
为半径画弧,两弧交于C点;
(4)连接 , ,则△ABC就是所求作的三角形.
a
A
B
BC
AC
2a
a
解析:可先作出长2a的线段,再作出底边,进而作出两腰的交点,连接交点和底边的端点即可.
5.如图所示,已知∠α,∠β和线段a,求作△ABC,使BC=a,∠B与∠α的补角相等,∠C=∠β.
解:第一步,作直线MN,并在上面取点B.如图(1)所示.
α
β
a
B
N
M
(1)
第二步,作∠MBP=∠α.如图(2)所示.
B
N
M
(2)
P
α
第三步,在BN上截取线段BC=a.如图(3)所示.
C
a
B
N
M
(3)
P
α
第四步,作∠BCQ=∠β,射线CQ,BP相交于点A,得到△ABC,如图(4)所示.
C
B
N
M
(4)
P
α
Q
A
β
谢 谢
三角形的尺规作图
豆豆书上的三角形被墨迹污染了一部分,你能帮他在作业本上画出一个与书上完全一样的三角形吗?
如何作一个三角形与已有的三角形一样呢?
情境思考
思 考
只用直尺(没有刻度)和圆规也可以画出一些图形。这种方法被称为尺规作图.
用直尺(没有刻度)和圆规作图,是一种具有特殊要求的作图方法,这种作图方法不必用具体数据,只是按给定图形进行作图,这也是它与画图的区别所在.
学习新知
画图一般不限定工具,既可以用直尺和圆规,也可以用其他辅助工具,比如量角器、三角板、刻度尺等。在尺规作图中,直尺的作用只能用来连接两点之间的线段或过两点画直线和射线.
已知三角形的三条边,求作这个三角形。
如图所示,已知线段a,b,c,求作△ABC,使AB=c,AC=b,BC=a.
b
a
c
作法:
(1)作一条线段AB=c;
(2)分别以A,B为圆心,以a,b为半径画弧,两弧交于C点;
(3)连接AC,BC。
如图所示的△ABC就是所求作的三角形。
b
a
c
C
A
B
如图所示,已知∠α,∠β,线段c,
求作△ABC,使∠A=∠α,∠B=∠β,AB=c.
α
β
已知三角形的两角和一边,求作三角形.
(1)已知三角形的两角及其夹边,求作这个三角形.
c
作法:(1)作∠DAF=∠α;(2)在射线AF上截取线段AB=c;(3)以B为顶点,以BA为一边,作∠ABE=∠β,BE交AD于点C.则△ABC就是所求作的三角形.
(2)已知两角和一角的对边,求作三角形.
如图所示,已知∠α,∠β,线段c,
求作△ABC,使∠A=∠α,∠B=∠β,AC=c.
β
c
α
先作出一个角等于∠α+∠β,通过反向延长角的一边得到它的补角,即三角形中的第三个内角∠γ。由此转换成已知∠α和∠γ及其这两角的夹边c,求作这个三角形.
已知三角形的两边和一角,求作三角形.
已知三角形的两边及夹角,求作这个三角形.
如图所示,已知线段a,b,∠α,
求作:△ABC,使BC=a,AB=b,∠ABC=∠α.
作法:(1)作∠DBE=∠α,(2)在射线BD,BE上分别截取BA=b,BC=a,(3)连接AC,△ABC就是所求作的三角形.
【规律方法小结】要掌握尺规作图的具体操作方法,按作图要求写作法时,要注意语言的规范性.
(1)用直尺作图时的规范性语言:
①过点 作直线 ,作线段 ,以点 为端点作射线 .②连接 ,以点 为端点作线段 ,延长线段 到点 ,使 = .
(2)用圆规作图时的规范性语言:
①以点 为圆心, 为半径作弧。②以点 为圆心, 为半径作弧,交 于点 .
课堂小结
1.作三角形的方法
作一个三角形与已知三角形全等,根据的就是三角形全等的条件。因此,作三角形时,所给的条件可以是三条边或两条边及夹角或两角及夹边或两角及一角的对边.
2.作三角形的步骤
在寻找作法的时候,一定要根据已知画出草图,确定作图步骤.
3.尺规作图的基本要求
①画图形;②写作法;③保留痕迹.
有些作图题,只要求保留痕迹,不用写作法.
检测反馈
1.尺规作图的画图工具是 ( )
A.刻度尺、量角器
B.三角板、量角器
C.直尺、量角器
D.没有刻度的直尺和圆规
D
解析:尺规作图的画图工具是没有刻度的直尺和圆规.故选D.
2.利用尺规作图,在下列条件中不能作出唯一直角三角形的是( )
A.已知两个锐角
B.已知一直角边和这边的对角
C.已知两条直角边
D.已知一个锐角和斜边
A
解析:A.因为已知两个锐角,而边长不确定,所以这样的三角形可作很多,而不是唯一的;B.符合全等三角形的判定“AAS”,能作出唯一直角三角形;C.符合全等三角形的判定“SAS”,能作出唯一直角三角形;D.符合全等三角形的判定“AAS”,能作出唯一直角三角形.故选A.
3.如图所示,△ABC是不等边三角形,DE=BC,以D,E为两个顶点作位置不同的三角形,使所作三角形与△ABC全等,这样的三角形最多可以作出( )
A.2个 B.4个 C.6个 D.8个
B
A
C
B
D
E
解析:可以作4个,分别是以D为圆心,AB长为半径作圆,以E为圆心,AC长为半径作圆.两圆相交于两点(DE上、下各一个),经过连接后可得到2个.然后以D为圆心,AC长为半径作圆,以E为圆心,AB长为半径作圆.两圆相交于两点(DE上、下各1个),经过连接后可得到2个.故选B.
4. 如图所示,已知线段a,用尺规作出△ABC,使AB=a,BC=AC=2a.
作法:
(1)先作一条线段等于2a,
(2)再作一条线段AB= ;
(3)分别以 、 为圆心,以
为半径画弧,两弧交于C点;
(4)连接 , ,则△ABC就是所求作的三角形.
a
A
B
BC
AC
2a
a
解析:可先作出长2a的线段,再作出底边,进而作出两腰的交点,连接交点和底边的端点即可.
5.如图所示,已知∠α,∠β和线段a,求作△ABC,使BC=a,∠B与∠α的补角相等,∠C=∠β.
解:第一步,作直线MN,并在上面取点B.如图(1)所示.
α
β
a
B
N
M
(1)
第二步,作∠MBP=∠α.如图(2)所示.
B
N
M
(2)
P
α
第三步,在BN上截取线段BC=a.如图(3)所示.
C
a
B
N
M
(3)
P
α
第四步,作∠BCQ=∠β,射线CQ,BP相交于点A,得到△ABC,如图(4)所示.
C
B
N
M
(4)
P
α
Q
A
β
谢 谢
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
