冀教版数学八年级上册17.3勾股定理 (2) 课件(共14张PPT)
文档属性
| 名称 | 冀教版数学八年级上册17.3勾股定理 (2) 课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-07 13:36:49 | ||
图片预览




文档简介
(共14张PPT)
(1)是证明方法最多的定理之一,有500多种证明方法;
(2)开创了“数形结合”的先河,被誉为“千古第一定理”;
(3)美国曾任总统加菲尔德给出一种证法,称为总统证明法;
作为在北京举行的第24届国际数学家大会的会标
创设情境 引出课题
科技赋能教育 构建魅力课堂
(4)揭示了直角三角形中“边与边”之间一种特殊关系;
毕达哥拉斯树
冀教版八年级上册
课题 勾股定理及其应用
科技赋能教育 构建魅力课堂
知识技能目标:会用面积法探究勾股定理(难点),理解直角三角形三边之间的数量关系,并会运用勾股定理及其逆定理解决简单的实际问题(重点)。
过程与方法目标:体验勾股定理的探究和运用过程,体会数形结合及由特殊到一般的数学思想。
情感态度目标:通过了解勾股定理的历史、文化背景,感受数学文化,在探究中培养同学们的民族自豪感。
学习目标
科技赋能教育 构建魅力课堂
相传公元前500年左右,毕达哥拉斯在朋友家做客时,发现朋友家地面上的三个正方形围成了一个等腰直角三角形,而且三边还存在一种特殊的数量关系。
毕达哥拉斯(公元前572~前492),古希腊著名的哲学家、数学家、天文学家。
尝试发现 探究新知
科技赋能教育 构建魅力课堂
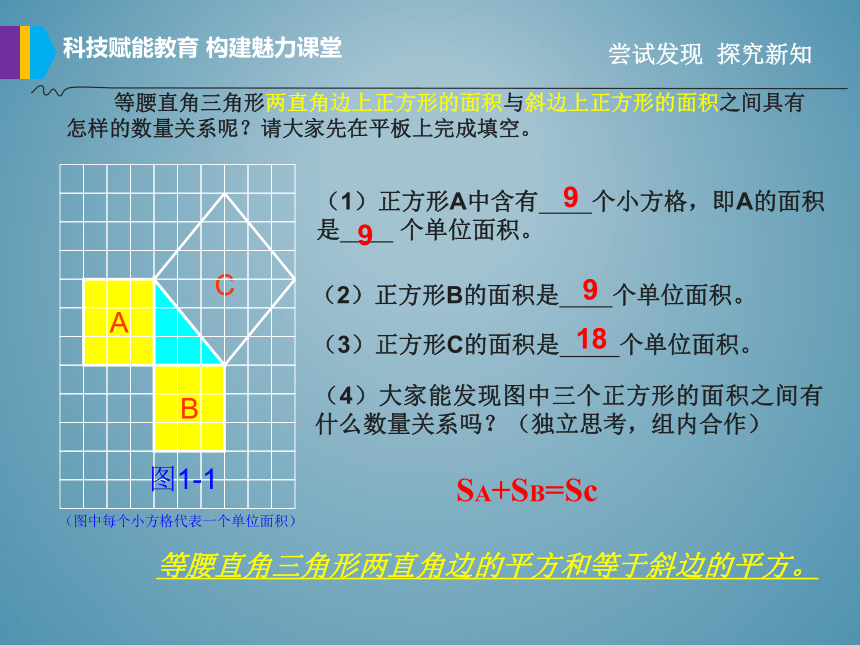
(图中每个小方格代表一个单位面积)
A
B
C
图1-1
(1)正方形A中含有 个小方格,即A的面积是 个单位面积。
(2)正方形B的面积是 个单位面积。
(3)正方形C的面积是 个单位面积。
9
9
9
18
等腰直角三角形两直角边上正方形的面积与斜边上正方形的面积之间具有怎样的数量关系呢?请大家先在平板上完成填空。
尝试发现 探究新知
科技赋能教育 构建魅力课堂
(4)大家能发现图中三个正方形的面积之间有什么数量关系吗?(独立思考,组内合作)
SA+SB=Sc
等腰直角三角形两直角边的平方和等于斜边的平方。
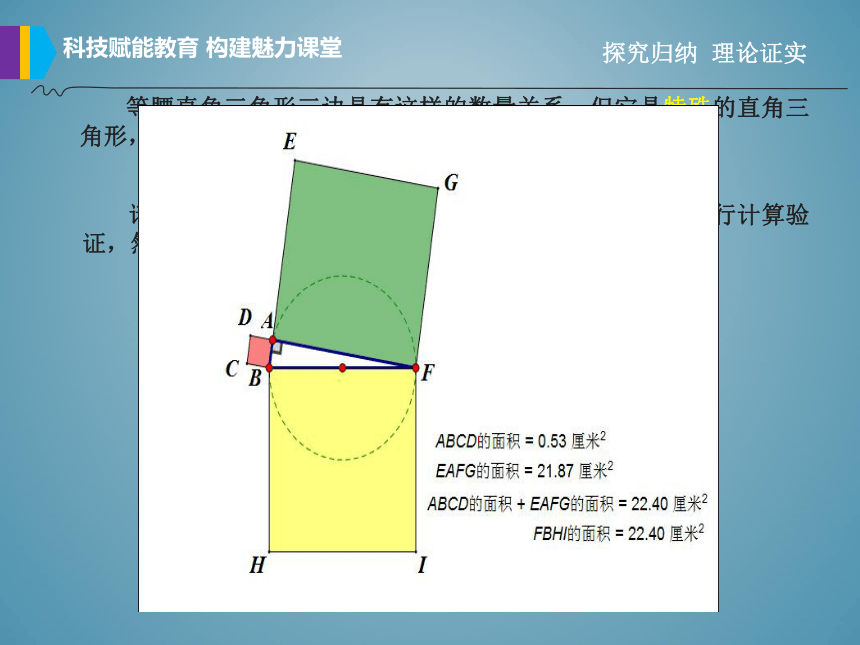
等腰直角三角形三边具有这样的数量关系,但它是特殊的直角三角形,那么,一般的直角三角形是否也有这样的性质呢?
探究归纳 理论证实
科技赋能教育 构建魅力课堂
请大家点击平板上推送的动图,类比上面的面积法,进行计算验证,然后组间分享。
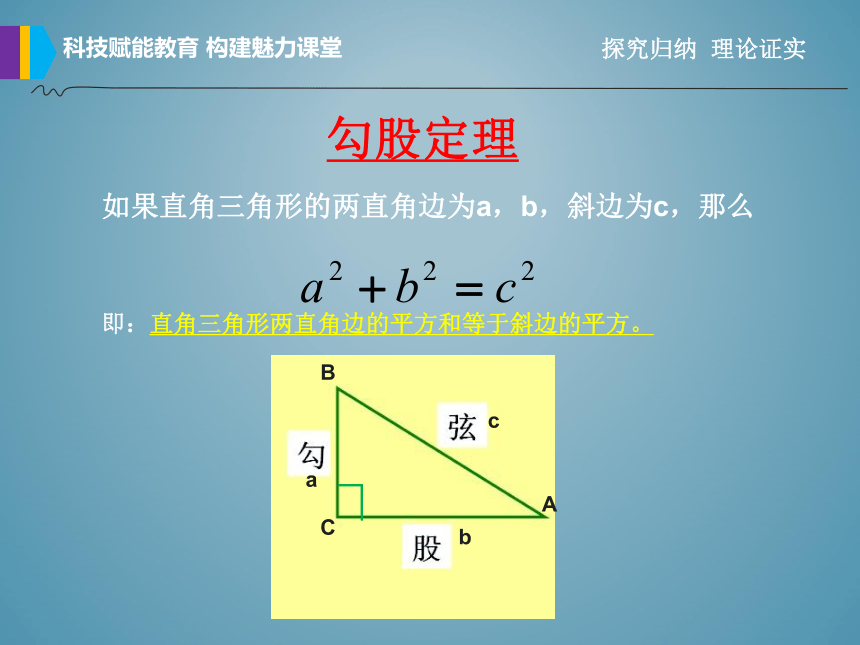
如果直角三角形的两直角边为a,b,斜边为c,那么
探究归纳 理论证实
勾股定理
科技赋能教育 构建魅力课堂
即:直角三角形两直角边的平方和等于斜边的平方。
A
B
C
a
b
c
思考 如果三角形的三边长a,b,c 满足a2+b2=c2 ,
那么这个三角形是否是直角三角形?
逆向思考 实验操作
科技赋能教育 构建魅力课堂
实验操作:
(1)画一画:下列各组数中的两数平方和等于第三数的
平方,分别以这些数为边长画出三角形(单位:cm),
它们是直角三角形吗?
① 2.5,6,6.5; ② 6,8,10.
(2)量一量:用量角器分别测量上述各三角形的最大角
的度数.
(3)想一想:请判断这些三角形的形状,并提出猜想.
演绎推理 形成定理
科技赋能教育 构建魅力课堂
作用:判定一个三角形三边满足什么条件时为直角三角形。
勾股定理的逆定理的定理
如果三角形的三边长a,b,c 满足a2+b2=c2,那么这个三角形是直角三角形。
走近历史
科技赋能教育 构建魅力课堂
大禹治水
赵爽注解《周髀算经》
毕达哥拉斯
中外很多名人都很青睐、向往勾股定理的证明和运用。(教学分享)
我国三国时期赵爽在注解《周髀算经》时,通过对图形进行移、补、凑、合而面积不变的方法证明了勾股定理,人们称为“赵爽弦图”。
走进历史
科技赋能教育 构建魅力课堂
课堂总结
科技赋能教育 构建魅力课堂
(1)本节课我们经历了怎样的学习过程?
(2)本节课我们学到了什么,有什么收获?
课堂总结
科技赋能教育 构建魅力课堂
1. 课本A组习题。(必做)
2. 探究勾股定理的其他证明方法。(选作)
科技赋能教育 构建魅力课堂
作业布置
(1)是证明方法最多的定理之一,有500多种证明方法;
(2)开创了“数形结合”的先河,被誉为“千古第一定理”;
(3)美国曾任总统加菲尔德给出一种证法,称为总统证明法;
作为在北京举行的第24届国际数学家大会的会标
创设情境 引出课题
科技赋能教育 构建魅力课堂
(4)揭示了直角三角形中“边与边”之间一种特殊关系;
毕达哥拉斯树
冀教版八年级上册
课题 勾股定理及其应用
科技赋能教育 构建魅力课堂
知识技能目标:会用面积法探究勾股定理(难点),理解直角三角形三边之间的数量关系,并会运用勾股定理及其逆定理解决简单的实际问题(重点)。
过程与方法目标:体验勾股定理的探究和运用过程,体会数形结合及由特殊到一般的数学思想。
情感态度目标:通过了解勾股定理的历史、文化背景,感受数学文化,在探究中培养同学们的民族自豪感。
学习目标
科技赋能教育 构建魅力课堂
相传公元前500年左右,毕达哥拉斯在朋友家做客时,发现朋友家地面上的三个正方形围成了一个等腰直角三角形,而且三边还存在一种特殊的数量关系。
毕达哥拉斯(公元前572~前492),古希腊著名的哲学家、数学家、天文学家。
尝试发现 探究新知
科技赋能教育 构建魅力课堂
(图中每个小方格代表一个单位面积)
A
B
C
图1-1
(1)正方形A中含有 个小方格,即A的面积是 个单位面积。
(2)正方形B的面积是 个单位面积。
(3)正方形C的面积是 个单位面积。
9
9
9
18
等腰直角三角形两直角边上正方形的面积与斜边上正方形的面积之间具有怎样的数量关系呢?请大家先在平板上完成填空。
尝试发现 探究新知
科技赋能教育 构建魅力课堂
(4)大家能发现图中三个正方形的面积之间有什么数量关系吗?(独立思考,组内合作)
SA+SB=Sc
等腰直角三角形两直角边的平方和等于斜边的平方。
等腰直角三角形三边具有这样的数量关系,但它是特殊的直角三角形,那么,一般的直角三角形是否也有这样的性质呢?
探究归纳 理论证实
科技赋能教育 构建魅力课堂
请大家点击平板上推送的动图,类比上面的面积法,进行计算验证,然后组间分享。
如果直角三角形的两直角边为a,b,斜边为c,那么
探究归纳 理论证实
勾股定理
科技赋能教育 构建魅力课堂
即:直角三角形两直角边的平方和等于斜边的平方。
A
B
C
a
b
c
思考 如果三角形的三边长a,b,c 满足a2+b2=c2 ,
那么这个三角形是否是直角三角形?
逆向思考 实验操作
科技赋能教育 构建魅力课堂
实验操作:
(1)画一画:下列各组数中的两数平方和等于第三数的
平方,分别以这些数为边长画出三角形(单位:cm),
它们是直角三角形吗?
① 2.5,6,6.5; ② 6,8,10.
(2)量一量:用量角器分别测量上述各三角形的最大角
的度数.
(3)想一想:请判断这些三角形的形状,并提出猜想.
演绎推理 形成定理
科技赋能教育 构建魅力课堂
作用:判定一个三角形三边满足什么条件时为直角三角形。
勾股定理的逆定理的定理
如果三角形的三边长a,b,c 满足a2+b2=c2,那么这个三角形是直角三角形。
走近历史
科技赋能教育 构建魅力课堂
大禹治水
赵爽注解《周髀算经》
毕达哥拉斯
中外很多名人都很青睐、向往勾股定理的证明和运用。(教学分享)
我国三国时期赵爽在注解《周髀算经》时,通过对图形进行移、补、凑、合而面积不变的方法证明了勾股定理,人们称为“赵爽弦图”。
走进历史
科技赋能教育 构建魅力课堂
课堂总结
科技赋能教育 构建魅力课堂
(1)本节课我们经历了怎样的学习过程?
(2)本节课我们学到了什么,有什么收获?
课堂总结
科技赋能教育 构建魅力课堂
1. 课本A组习题。(必做)
2. 探究勾股定理的其他证明方法。(选作)
科技赋能教育 构建魅力课堂
作业布置
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
