冀教版数学八年级上册13.3 全等三角形的判定-第一课时 课件(共23张PPT)
文档属性
| 名称 | 冀教版数学八年级上册13.3 全等三角形的判定-第一课时 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 157.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-07 13:37:39 | ||
图片预览





文档简介
(共23张PPT)
第一课时
全等三角形的判定
(1)全等三角形 相等, 相等.
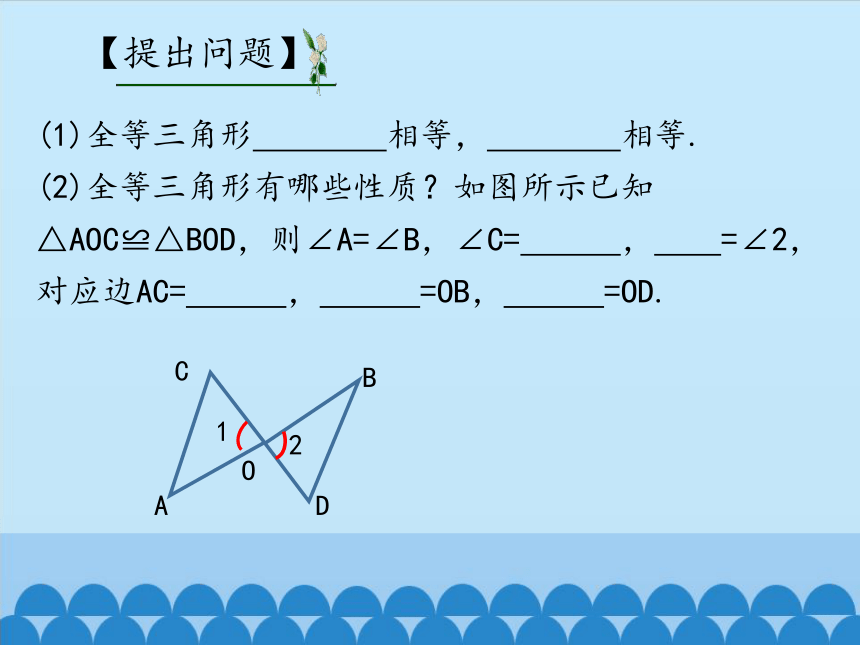
(2)全等三角形有哪些性质?如图所示已知
△AOC≌△BOD,则∠A=∠B,∠C= , =∠2,对应边AC= , =OB, =OD.
D
A
B
C
O
1
2
【提出问题】
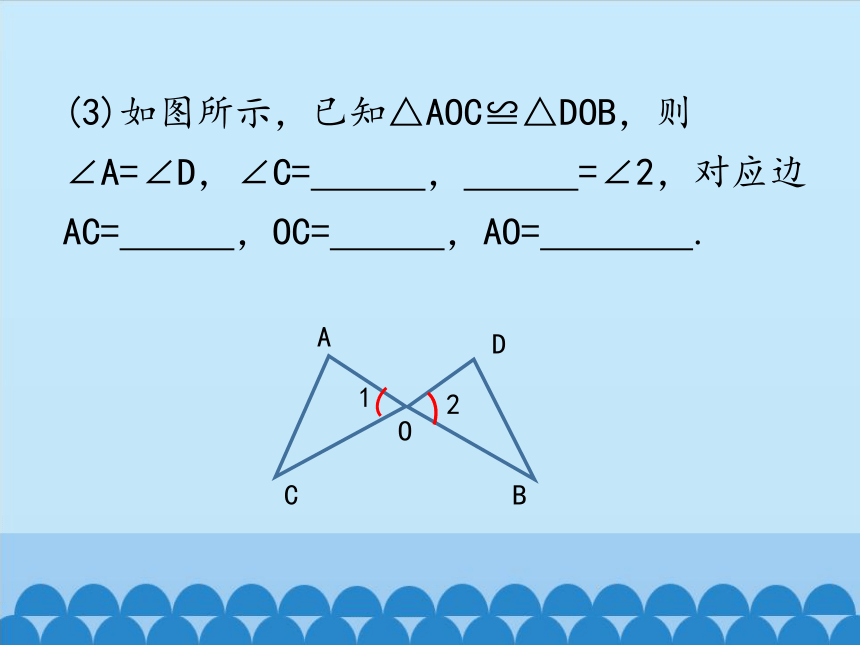
(3)如图所示,已知△AOC≌△DOB,则∠A=∠D,∠C= , =∠2,对应边AC= ,OC= ,AO= .
B
C
D
A
O
1
2
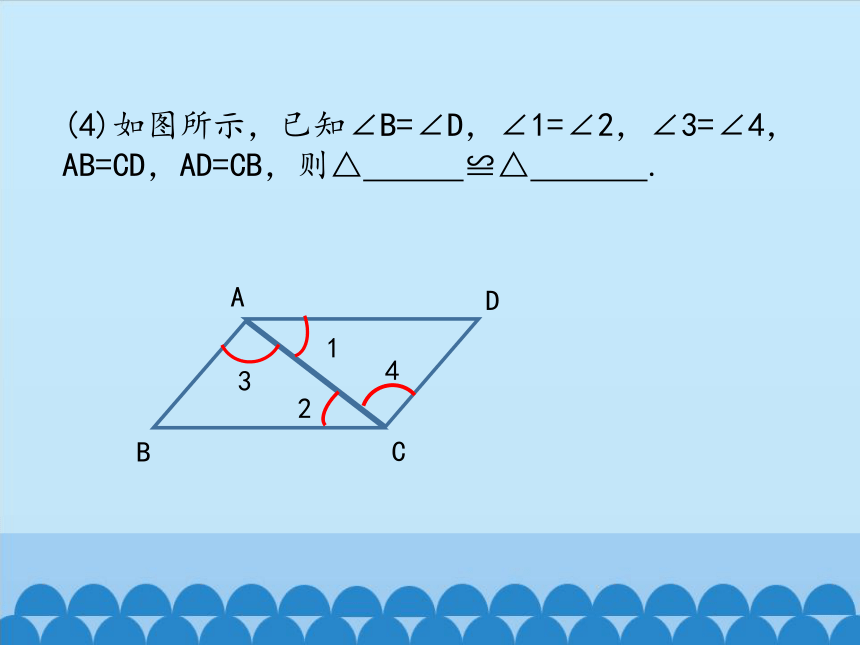
(4)如图所示,已知∠B=∠D,∠1=∠2,∠3=∠4,AB=CD,AD=CB,则△ ≌△ .
C
B
D
A
1
2
3
4
(5)判定两个三角形全等,依定义必须满足( )
A.三边对应相等
B.三角对应相等
C.三边对应相等和三角对应相等
D.不能确定
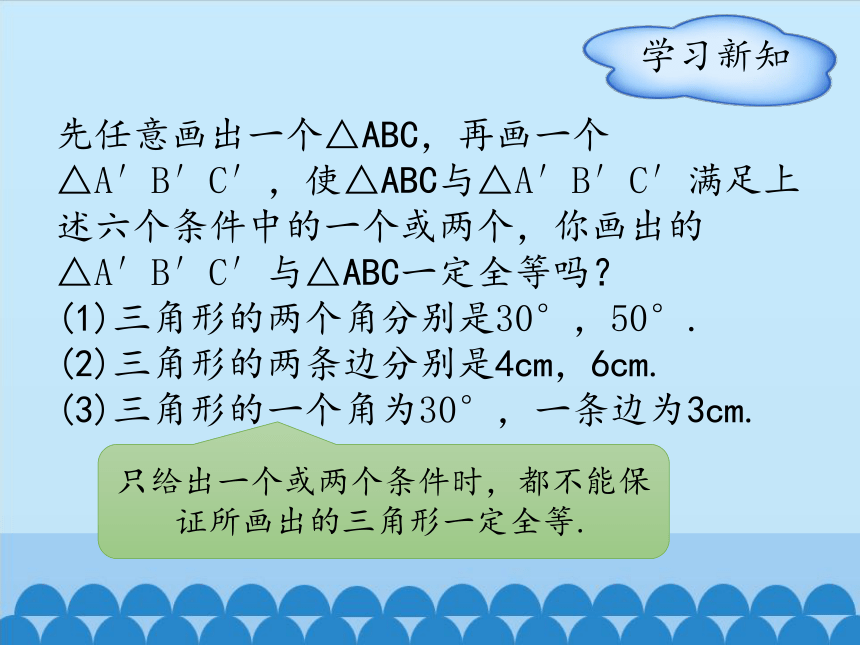
先任意画出一个△ABC,再画一个△A′B′C′,使△ABC与△A′B′C′满足上述六个条件中的一个或两个,你画出的△A′B′C′与△ABC一定全等吗?
(1)三角形的两个角分别是30°,50°.
(2)三角形的两条边分别是4cm,6cm.
(3)三角形的一个角为30°,一条边为3cm.
学习新知
只给出一个或两个条件时,都不能保证所画出的三角形一定全等.
已知△ABC,再任意画出一个△A′B′C′,使A′B′=AB,B′C′=BC,C′A′=CA。把画好的△A′B′C′剪下,放到△ABC上,它们全等吗
三边分别相等的两个三角形全等.
应用时的简写方法:“边边边”或“SSS”.
小组讨论下面问题:
(1)在两个三角形中,有一个角对应相等,或一条边对应相等,这两个三角形是否一定全等?有两个角对应相等,或两条边对应相等,或一个角和一条边分别对应相等,情况怎样?有三个角对应相等的情况呢?
议一议
(2)用来判断两个三角形全等的条件,只有以下三种情况才有可能:三条边对应相等,或两条边和一个角分别对应相等,或两个角和一条边分别对应相等。你认为这些说法对吗?
通过画图可以发现,满足上述六个条件中的一个或两个,△ABC与△A′B′C′不一定全等。满足上述六个条件中的三个,能保证△ABC与△A′B′C′全等吗?
分小组活动:
(1)用一根长13cm的细铁丝,折成一个边长分别是3cm,4cm,6cm的三角形。把你做的三角形和同学做的三角形进行比较,它们能重合吗?
(2)和同学一起每人用一根13cm长的细铁丝,余下1cm,用其余部分折成一个边长分别是3cm,4cm,5cm的三角形,再和同学做的三角形进行比较,它们能重合吗?
(3)每人用一根细铁丝,任取一组能构成三角形的三边长的数据,和同桌分别按这些数据折三角形,折成的两个三角形能重合吗?
(4)先任意画出一个△ABC,再画一个△A′B′C′,使A′B′=AB,B′C′=BC,C′A′=CA。把画好的△A′B′C′剪下,放到△ABC上,它们全等吗?
文字 符号 图形
三边对应相等的两个三角形全等 如果AB=A′B′,BC=B′C′,AC=A′C′,那么△ABC≌△A′B′C′
A
B
C
B′
A′
C′
将三根木条钉成一个三角形框架,在拉动时,这个三角形框架的形状、大小就不变了。就是说,三角形的三边确定了,这个三角形的形状、大小也就确定了。这里就用到了上面的结论。
用上面的结论可以判断两个三角形全等。
用四根木条钉成四边形框架时,在拉动时,它的形状会改变,所以四边形具有不稳定性。
判断两个三角形全等的推理过程,叫做证明三角形全等。
如图所示,△ABC是一个钢架,AB=AC,AD是连接点A与BC中点D的支架。
求证△ABD≌△ACD.
C
B
A
D
例题讲解
证明:∵D是BC的中点,
∴BD=CD。
在△ABD和△ACD中,
AB=AC,
BD=CD,
AD=AD.
∴△ABD≌△ACD(SSS).
(1)有的题目可以直接从图中找到全等的条件,而有的题目的条件则隐含在题设或图形之中,所以一定要认真读图,准确把握题意,找准所需的条件.
(2)数形结合思想:将“数”与“形”结合起来进行分析、研究,这是解决问题的一种思想方法.
知识拓展
课堂小结
两个三角形如果三边对应相等,那么这两个三角形全等,称为“边边边”基本事实,从而可知三角形具有稳定性这一性质。
利用两三角形全等,可进行一些相关的计算和证明。
检测反馈
1.如图所示,B,D,C,E在一条直线上,且BC=DE,AC=FD,AE=FB,则BD= ,△ACE≌ ,理由是 .
EC
△FDB
SSS
A
C
D
E
F
B
解析:
∵BC=BD+CD,DE=EC+CD,BC=DE,∴BD=EC.
又∵AC=FD,AE=FB,
∴△ACE≌△FDB(SSS).
2.如图所示,点B,E,C,F在一条直线上,AB=DE,BE=CF,请添加一个条件: ,使△ABC≌△DEF(SSS).
AC=DF
D
A
F
C
E
B
解析:添加AC=DF.
∵BE=CF,∴BC=EF,∵在△ABC和△DEF中,
∴△ABC≌△DEF(SSS).
故填AC=DF.
3.如图所示,在△ABC中,AB=AC,BE=CE,则由“SSS”可以判定 .(填序号)
③
①△ABD≌△ACD; ②△BDE≌△CDE;
③△ABE≌△ACE.
A
D
B
E
C
解析:AE为△ABE与△ACE的公共边,
∵AB=AC,BE=CE,AE=AE,
∴△ABE≌△ACE.故填③.
4.如图所示,在四边形ABCD中,AB=AD,CB=CD.求证∠B=∠D.
证明:连接AC,在△ABC和△ADC中,
AB=AD,
CB=CD,
AC=AC,
∴△ABC≌△ADC,
∴∠B=∠D.
解析:先连接AC,由于AB=AD,CB=CD,AC=AC,
∴可利用“SSS”证明△ABC≌△ADC,∴∠B=∠D.
谢 谢
第一课时
全等三角形的判定
(1)全等三角形 相等, 相等.
(2)全等三角形有哪些性质?如图所示已知
△AOC≌△BOD,则∠A=∠B,∠C= , =∠2,对应边AC= , =OB, =OD.
D
A
B
C
O
1
2
【提出问题】
(3)如图所示,已知△AOC≌△DOB,则∠A=∠D,∠C= , =∠2,对应边AC= ,OC= ,AO= .
B
C
D
A
O
1
2
(4)如图所示,已知∠B=∠D,∠1=∠2,∠3=∠4,AB=CD,AD=CB,则△ ≌△ .
C
B
D
A
1
2
3
4
(5)判定两个三角形全等,依定义必须满足( )
A.三边对应相等
B.三角对应相等
C.三边对应相等和三角对应相等
D.不能确定
先任意画出一个△ABC,再画一个△A′B′C′,使△ABC与△A′B′C′满足上述六个条件中的一个或两个,你画出的△A′B′C′与△ABC一定全等吗?
(1)三角形的两个角分别是30°,50°.
(2)三角形的两条边分别是4cm,6cm.
(3)三角形的一个角为30°,一条边为3cm.
学习新知
只给出一个或两个条件时,都不能保证所画出的三角形一定全等.
已知△ABC,再任意画出一个△A′B′C′,使A′B′=AB,B′C′=BC,C′A′=CA。把画好的△A′B′C′剪下,放到△ABC上,它们全等吗
三边分别相等的两个三角形全等.
应用时的简写方法:“边边边”或“SSS”.
小组讨论下面问题:
(1)在两个三角形中,有一个角对应相等,或一条边对应相等,这两个三角形是否一定全等?有两个角对应相等,或两条边对应相等,或一个角和一条边分别对应相等,情况怎样?有三个角对应相等的情况呢?
议一议
(2)用来判断两个三角形全等的条件,只有以下三种情况才有可能:三条边对应相等,或两条边和一个角分别对应相等,或两个角和一条边分别对应相等。你认为这些说法对吗?
通过画图可以发现,满足上述六个条件中的一个或两个,△ABC与△A′B′C′不一定全等。满足上述六个条件中的三个,能保证△ABC与△A′B′C′全等吗?
分小组活动:
(1)用一根长13cm的细铁丝,折成一个边长分别是3cm,4cm,6cm的三角形。把你做的三角形和同学做的三角形进行比较,它们能重合吗?
(2)和同学一起每人用一根13cm长的细铁丝,余下1cm,用其余部分折成一个边长分别是3cm,4cm,5cm的三角形,再和同学做的三角形进行比较,它们能重合吗?
(3)每人用一根细铁丝,任取一组能构成三角形的三边长的数据,和同桌分别按这些数据折三角形,折成的两个三角形能重合吗?
(4)先任意画出一个△ABC,再画一个△A′B′C′,使A′B′=AB,B′C′=BC,C′A′=CA。把画好的△A′B′C′剪下,放到△ABC上,它们全等吗?
文字 符号 图形
三边对应相等的两个三角形全等 如果AB=A′B′,BC=B′C′,AC=A′C′,那么△ABC≌△A′B′C′
A
B
C
B′
A′
C′
将三根木条钉成一个三角形框架,在拉动时,这个三角形框架的形状、大小就不变了。就是说,三角形的三边确定了,这个三角形的形状、大小也就确定了。这里就用到了上面的结论。
用上面的结论可以判断两个三角形全等。
用四根木条钉成四边形框架时,在拉动时,它的形状会改变,所以四边形具有不稳定性。
判断两个三角形全等的推理过程,叫做证明三角形全等。
如图所示,△ABC是一个钢架,AB=AC,AD是连接点A与BC中点D的支架。
求证△ABD≌△ACD.
C
B
A
D
例题讲解
证明:∵D是BC的中点,
∴BD=CD。
在△ABD和△ACD中,
AB=AC,
BD=CD,
AD=AD.
∴△ABD≌△ACD(SSS).
(1)有的题目可以直接从图中找到全等的条件,而有的题目的条件则隐含在题设或图形之中,所以一定要认真读图,准确把握题意,找准所需的条件.
(2)数形结合思想:将“数”与“形”结合起来进行分析、研究,这是解决问题的一种思想方法.
知识拓展
课堂小结
两个三角形如果三边对应相等,那么这两个三角形全等,称为“边边边”基本事实,从而可知三角形具有稳定性这一性质。
利用两三角形全等,可进行一些相关的计算和证明。
检测反馈
1.如图所示,B,D,C,E在一条直线上,且BC=DE,AC=FD,AE=FB,则BD= ,△ACE≌ ,理由是 .
EC
△FDB
SSS
A
C
D
E
F
B
解析:
∵BC=BD+CD,DE=EC+CD,BC=DE,∴BD=EC.
又∵AC=FD,AE=FB,
∴△ACE≌△FDB(SSS).
2.如图所示,点B,E,C,F在一条直线上,AB=DE,BE=CF,请添加一个条件: ,使△ABC≌△DEF(SSS).
AC=DF
D
A
F
C
E
B
解析:添加AC=DF.
∵BE=CF,∴BC=EF,∵在△ABC和△DEF中,
∴△ABC≌△DEF(SSS).
故填AC=DF.
3.如图所示,在△ABC中,AB=AC,BE=CE,则由“SSS”可以判定 .(填序号)
③
①△ABD≌△ACD; ②△BDE≌△CDE;
③△ABE≌△ACE.
A
D
B
E
C
解析:AE为△ABE与△ACE的公共边,
∵AB=AC,BE=CE,AE=AE,
∴△ABE≌△ACE.故填③.
4.如图所示,在四边形ABCD中,AB=AD,CB=CD.求证∠B=∠D.
证明:连接AC,在△ABC和△ADC中,
AB=AD,
CB=CD,
AC=AC,
∴△ABC≌△ADC,
∴∠B=∠D.
解析:先连接AC,由于AB=AD,CB=CD,AC=AC,
∴可利用“SSS”证明△ABC≌△ADC,∴∠B=∠D.
谢 谢
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
