冀教版数学八年级上册17.3勾股定理 教案(表格式)
文档属性
| 名称 | 冀教版数学八年级上册17.3勾股定理 教案(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 529.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-07 00:00:00 | ||
图片预览


文档简介
《勾股定理》教学设计
学校名称
课例名称 勾股定理(第1课时) 教师姓名
学段学科 初中数学 教材版本 冀教版
章节 第17章第3节 年级 八年级
教学目标 知识与技能 掌握勾股定理,能熟练地运用勾股定理并可以已知直角三角形两边求第三边;发展对图形性质和数量关系猜想和检验的能力,增强思维能力。 过程与方法 经历探究和验证勾股定理的过程, 体验“观察—猜想—求证—验证”的过程。 情感态度价值观 通过了解我国在勾股定理研究方面的成就,激发热爱祖国,热爱中国悠久文化的感情。
教学重难点 重点:探究并证明勾股定理。 难点:勾股定理的探究和证明。
学情分析 1.学生是八年级的学生,有一定地逻辑思维能力及自学能力。 2.这节课安排是在直角三角形之后,并且熟知基本图形的面积公式,有利于验证勾股定理 3.学生对几何图形的观察能力和几何的分析能力已经逐步形成
教学方法 在教学中采用“引导探索法”,由浅入深,以导为主,进行探究性学习,鼓励合作交流,培养“动手,动脑,动口”的习惯和能力.
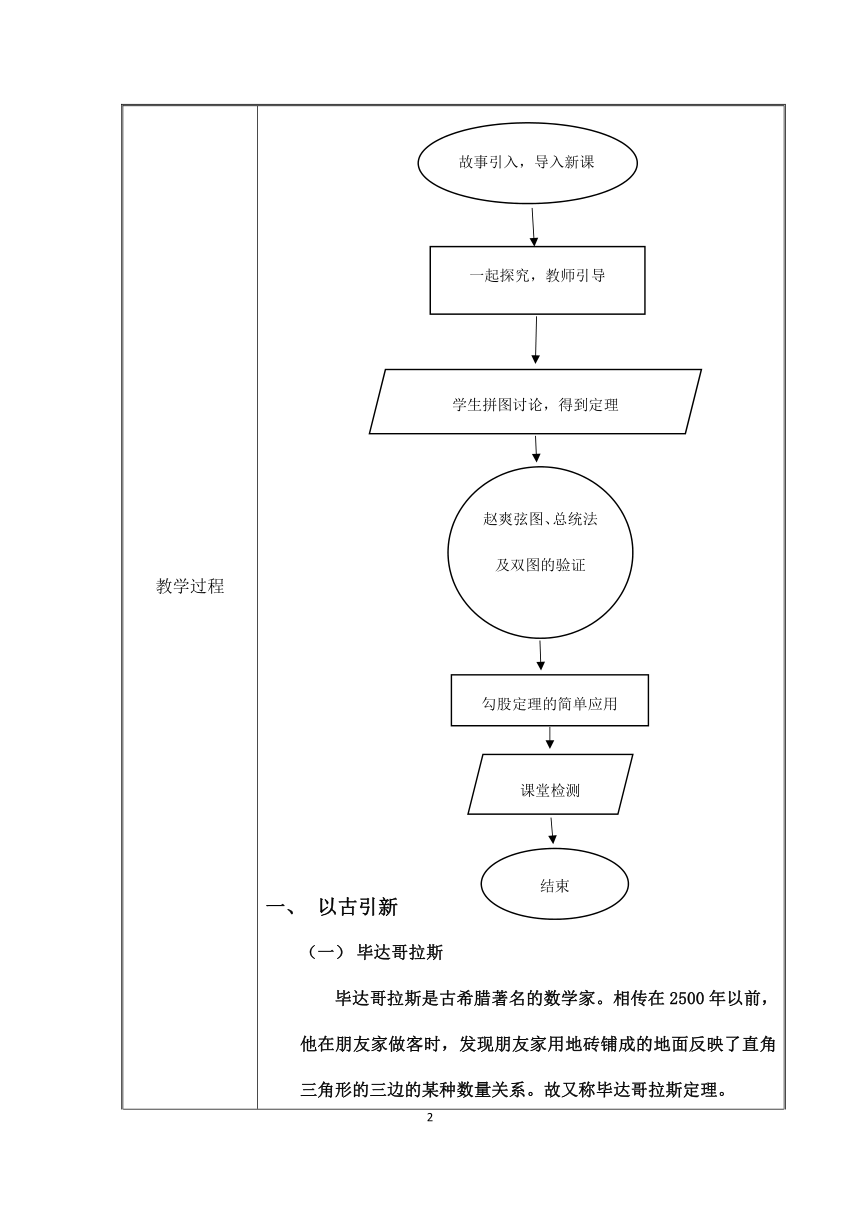
教学过程 教学过程 教学过程 教学过程 教学过程 教学过程 教学流程图 (
故事引入,导入新课
) (
一起探究,教师引导
) (
学生拼图讨论,得到定理
) (
赵爽弦图、总统法及双图的验证
) (
勾股定理的简单应用
) (
课堂检测
) (
结束
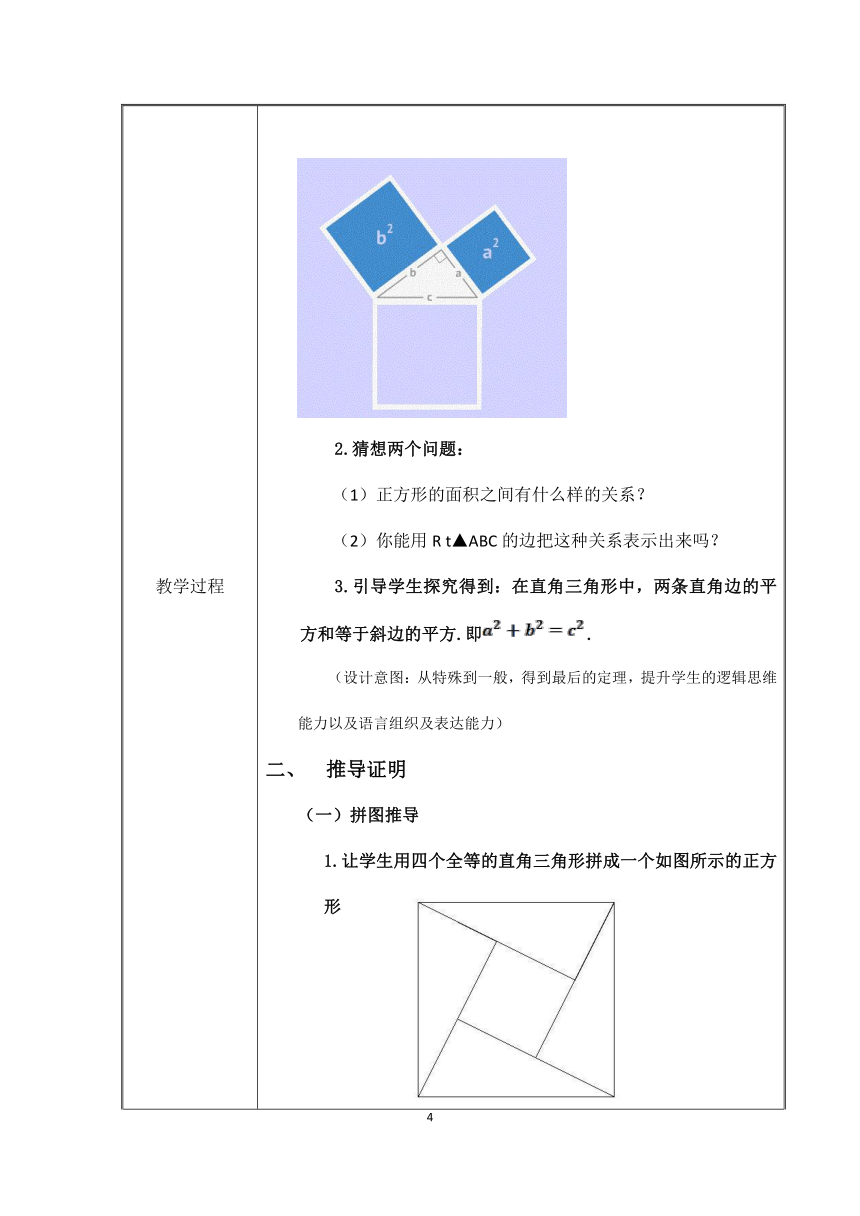
) 以古引新 毕达哥拉斯 毕达哥拉斯是古希腊著名的数学家。相传在2500年以前,他在朋友家做客时,发现朋友家用地砖铺成的地面反映了直角三角形的三边的某种数量关系。故又称毕达哥拉斯定理。 商高 更早地,在中国,就记载着商高关于勾股形问题对周公的谈话:“故折矩以为勾广三,股修四,径隅五。” (设计意图:以故事的形式让学生初步对勾股产生兴趣,并且有一定的了解) 猜想探究 (一)观察图片 探讨正方形面积的关系以及正方形所围成的三角形是一个什么样的三角形。 猜想结论 1.实验猜想勾股定理的动态图 2.猜想两个问题: (1)正方形的面积之间有什么样的关系? (2)你能用R t▲ABC的边把这种关系表示出来吗? 3.引导学生探究得到:在直角三角形中,两条直角边的平方和等于斜边的平方.即. (设计意图:从特殊到一般,得到最后的定理,提升学生的逻辑思维能力以及语言组织及表达能力) 推导证明 (一)拼图推导 (
D
A
E
B
G
F
H
C
c
b
a
)1.让学生用四个全等的直角三角形拼成一个如图所示的正方形 (赵爽弦图) (
设未知量
)2.在拼图的过程中,明白几何图形面积之间的关系,从而利用代数的思想,验证勾股定理,并从中归纳证明方法: (
找等量关系
) (二)代数论证 通过上面的证明过程,自己验证总统法 得到 最后得到 归纳定理 明确勾、股、弦的概念以及勾股定理 勾股定理:如果直角三角形两直角边分别为a,b,斜边为c,那么 也可叙述为: 直角三角形两直角边的平方和等于斜边的平方. 验证定理 比较两图的区别,验证 得到勾股定理的重要性,是沟通几何和代数的桥梁. 简单应用 (一)变形 有得到三个变形的式子,利用变式去解决问题. (二)检测 1.已知Rt▲ABC中,直角边a=5,b=12,斜边为c= 2.已知Rt▲ABC中,直角边a=3m,b=4m,斜边为c= 3.已知Rt▲ABC中,a=2,b=5,c= (1)当a和b均为直角边时 (2)当a为直角边,b为斜边时 课堂小结 这节课我们主要学习了什么内容?有哪些收获? 1.勾股定理 2.勾股定理的代数证明方法 3.在直角三角形中,如果知道两条边的长,会求第三边 体验勾股的美及应用 (一)图片赏析 1.毕达哥拉斯数及几何画板的动态图 2.根号x的螺旋 (二)常见的勾股数总结 34551213724258151794041123537
课后作业 P152 练习 1 A 组 1,3 B 组 1
1
- 6 -
2
学校名称
课例名称 勾股定理(第1课时) 教师姓名
学段学科 初中数学 教材版本 冀教版
章节 第17章第3节 年级 八年级
教学目标 知识与技能 掌握勾股定理,能熟练地运用勾股定理并可以已知直角三角形两边求第三边;发展对图形性质和数量关系猜想和检验的能力,增强思维能力。 过程与方法 经历探究和验证勾股定理的过程, 体验“观察—猜想—求证—验证”的过程。 情感态度价值观 通过了解我国在勾股定理研究方面的成就,激发热爱祖国,热爱中国悠久文化的感情。
教学重难点 重点:探究并证明勾股定理。 难点:勾股定理的探究和证明。
学情分析 1.学生是八年级的学生,有一定地逻辑思维能力及自学能力。 2.这节课安排是在直角三角形之后,并且熟知基本图形的面积公式,有利于验证勾股定理 3.学生对几何图形的观察能力和几何的分析能力已经逐步形成
教学方法 在教学中采用“引导探索法”,由浅入深,以导为主,进行探究性学习,鼓励合作交流,培养“动手,动脑,动口”的习惯和能力.
教学过程 教学过程 教学过程 教学过程 教学过程 教学过程 教学流程图 (
故事引入,导入新课
) (
一起探究,教师引导
) (
学生拼图讨论,得到定理
) (
赵爽弦图、总统法及双图的验证
) (
勾股定理的简单应用
) (
课堂检测
) (
结束
) 以古引新 毕达哥拉斯 毕达哥拉斯是古希腊著名的数学家。相传在2500年以前,他在朋友家做客时,发现朋友家用地砖铺成的地面反映了直角三角形的三边的某种数量关系。故又称毕达哥拉斯定理。 商高 更早地,在中国,就记载着商高关于勾股形问题对周公的谈话:“故折矩以为勾广三,股修四,径隅五。” (设计意图:以故事的形式让学生初步对勾股产生兴趣,并且有一定的了解) 猜想探究 (一)观察图片 探讨正方形面积的关系以及正方形所围成的三角形是一个什么样的三角形。 猜想结论 1.实验猜想勾股定理的动态图 2.猜想两个问题: (1)正方形的面积之间有什么样的关系? (2)你能用R t▲ABC的边把这种关系表示出来吗? 3.引导学生探究得到:在直角三角形中,两条直角边的平方和等于斜边的平方.即. (设计意图:从特殊到一般,得到最后的定理,提升学生的逻辑思维能力以及语言组织及表达能力) 推导证明 (一)拼图推导 (
D
A
E
B
G
F
H
C
c
b
a
)1.让学生用四个全等的直角三角形拼成一个如图所示的正方形 (赵爽弦图) (
设未知量
)2.在拼图的过程中,明白几何图形面积之间的关系,从而利用代数的思想,验证勾股定理,并从中归纳证明方法: (
找等量关系
) (二)代数论证 通过上面的证明过程,自己验证总统法 得到 最后得到 归纳定理 明确勾、股、弦的概念以及勾股定理 勾股定理:如果直角三角形两直角边分别为a,b,斜边为c,那么 也可叙述为: 直角三角形两直角边的平方和等于斜边的平方. 验证定理 比较两图的区别,验证 得到勾股定理的重要性,是沟通几何和代数的桥梁. 简单应用 (一)变形 有得到三个变形的式子,利用变式去解决问题. (二)检测 1.已知Rt▲ABC中,直角边a=5,b=12,斜边为c= 2.已知Rt▲ABC中,直角边a=3m,b=4m,斜边为c= 3.已知Rt▲ABC中,a=2,b=5,c= (1)当a和b均为直角边时 (2)当a为直角边,b为斜边时 课堂小结 这节课我们主要学习了什么内容?有哪些收获? 1.勾股定理 2.勾股定理的代数证明方法 3.在直角三角形中,如果知道两条边的长,会求第三边 体验勾股的美及应用 (一)图片赏析 1.毕达哥拉斯数及几何画板的动态图 2.根号x的螺旋 (二)常见的勾股数总结 34551213724258151794041123537
课后作业 P152 练习 1 A 组 1,3 B 组 1
1
- 6 -
2
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
