高中物理人教版(2019)选择性必修第一册 第2章 第4节 单摆同步练习(含答案)
文档属性
| 名称 | 高中物理人教版(2019)选择性必修第一册 第2章 第4节 单摆同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 117.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-11-07 12:35:24 | ||
图片预览

文档简介
第4节 单摆
1.[多选]关于单摆做简谐运动,下列说法正确的是 ( )
A.经过平衡位置时所受的合力为0
B.经过平衡位置时所受的回复力为0
C.回复力是重力和摆线拉力的合力
D.回复力是重力沿圆弧切线方向的分力
2.摆长是1 m的单摆在某地区振动周期是2 s,则在同一地区 ( )
A.摆长是0.5 m的单摆的周期是0.707 s
B.摆长是0.5 m的单摆的周期是1 s
C.周期是1 s的单摆的摆长为2 m
D.周期是4 s的单摆的摆长为4 m
3.[多选]如图所示,A,B分别为单摆做简谐运动时摆球的不同位置。其中A处为单摆摆动的最高位置,虚线为过悬点的竖直线。以单摆最低位置为重力势能零点,则单摆在摆动过程中 ( )
A.位于B处时动能最大
B.位于A处时势能最大
C.在A处的势能大于在B处的动能
D.在B处的机械能大于在A处的机械能
4.某一单摆原来的周期是2 s,在下列情况下,周期有无变化?如有变化,变为多少?
(1)摆长减为原长的。
(2)摆球的质量减为原来的。
(3)振幅减为原来的。
(4)重力加速度减为原来的。
5.已知单摆的摆长是1 m时,摆动周期是2 s。当摆长改变为0.81 m时,摆动周期是多少?要使摆动周期为4 s,摆长应是多少?
6.如图所示,光滑圆槽的半径R远大于小球运动的弧长。甲、乙、丙三个小球(均可视为质点)同时由静止释放,开始时,甲球比乙球离槽最低点O远些,丙球在槽的圆心处。请比较它们第一次到达点O的先后顺序,并说明理由。
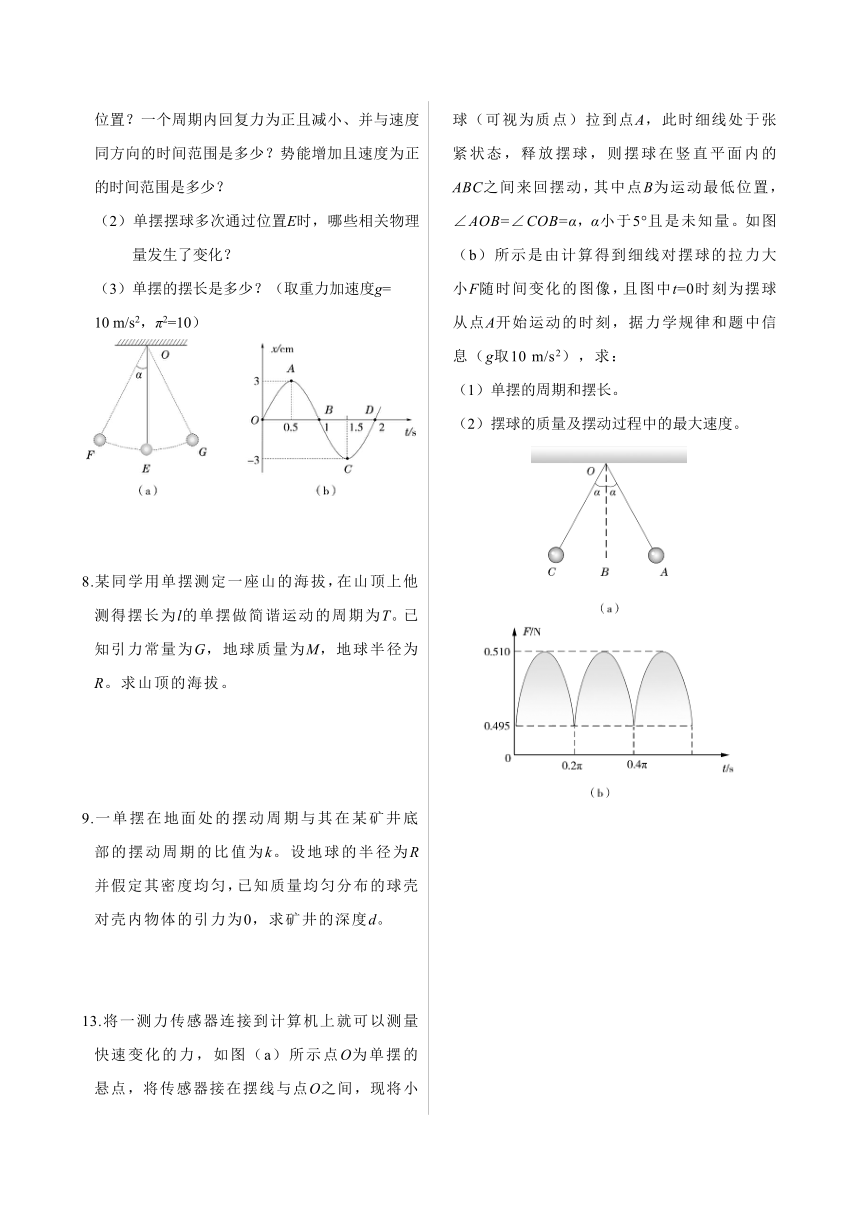
7.某单摆及其振动图像如图所示。
(1)若取从E指向G为正方向,α为最大摆角,则图像中点O、A、B、C、D分别对应单摆中的哪个位置?一个周期内回复力为正且减小、并与速度同方向的时间范围是多少?势能增加且速度为正的时间范围是多少?
(2)单摆摆球多次通过位置E时,哪些相关物理量发生了变化?
(3)单摆的摆长是多少?(取重力加速度g=
10 m/s2,π2=10)
8.某同学用单摆测定一座山的海拔,在山顶上他测得摆长为l的单摆做简谐运动的周期为T。已知引力常量为G,地球质量为M,地球半径为R。求山顶的海拔。
9.一单摆在地面处的摆动周期与其在某矿井底部的摆动周期的比值为k。设地球的半径为R并假定其密度均匀,已知质量均匀分布的球壳对壳内物体的引力为0,求矿井的深度d。
13.将一测力传感器连接到计算机上就可以测量快速变化的力,如图(a)所示点O为单摆的悬点,将传感器接在摆线与点O之间,现将小球(可视为质点)拉到点A,此时细线处于张紧状态,释放摆球,则摆球在竖直平面内的ABC之间来回摆动,其中点B为运动最低位置,∠AOB=∠COB=α,α小于5°且是未知量。如图(b)所示是由计算得到细线对摆球的拉力大小F随时间变化的图像,且图中t=0时刻为摆球从点A开始运动的时刻,据力学规律和题中信息(g取10 m/s2),求:
(1)单摆的周期和摆长。
(2)摆球的质量及摆动过程中的最大速度。
第4节 单摆
参考答案
BD
D
BC
解:由单摆周期公式T=知,单摆的周期与摆球质量和振幅无关,故(2)(3)两种情况,周期不变。
(1)中,由周期公式得T1==1 s。
(4)中,由周期公式得T2=2T=4 s。
解:由单摆周期公式T=得, =,则T′=0.9T=1.8 s,由单摆周期公式T=得, =,则L″=4L=4 m。
解:甲、乙两球沿光滑圆槽做简谐运动,等效摆长为R,周期相同,甲、乙两球同时到达点O,需要的时间t1===,
丙球做自由落体运动,由R=,得t2==·,
,即t1>t2,故丙球最先到达点O,甲、乙两球同时到达点O。
解:(1)单摆的小角度摆动是简谐运动,从振动图像看出:
O点对应平衡位置,对应单摆中的E点;
A点位于正向最大位移处,对应单摆中的G点;
B点位于平衡位置,对应单摆中的E点;
C点位于负向最大位移处,对应单摆中的F点;
D点位于平衡位置,对应单摆中的E点。
由题图可知,单摆的周期为2 s,F回为正且减小,应该位于平衡位置左侧且正衡位置,即由F→E运动,对应时间范围应为1.5~2.0 s。
势能增加且速度为正的时间范围为0~0.5 s。
(2)摆球多次通过同一位置E时,位移是相同的,为0,摆线弹力相同,回复力(加速度)相同,速度大小相等,动能是相同的,但速度方向不同,故动量不同。
即速度、动量发生了变化。
(3)由T=,得l===1 m。
解:设山顶上的重力加速度为g′,则有T=,得出g′= ①
设山顶的海拔为h,则有mg′= ②
联立①②式解得h=。
解:在地面上有mg=,M=πρR3,解得g=πGρR
单摆的周期T=2π
在矿井底部单摆的周期T′=,
此处mg′=,半径为R-d的地球对应的质量M′=,解得g′=,
,,即=k2,得出d=(1-k2)R。
解:(1)由图(b)可知,周期T=0.4π s,由单摆周期公式T=得L== m=0.4 m。
(2) 在最高点A,有Fmin=mgcos α=0.495 N,在最低点B,有Fmax-mg=,从A到B,机械能守恒,有mgL(1-cos α)=,联立得m=0.05 kg,v≈0.283 m/s。
1.[多选]关于单摆做简谐运动,下列说法正确的是 ( )
A.经过平衡位置时所受的合力为0
B.经过平衡位置时所受的回复力为0
C.回复力是重力和摆线拉力的合力
D.回复力是重力沿圆弧切线方向的分力
2.摆长是1 m的单摆在某地区振动周期是2 s,则在同一地区 ( )
A.摆长是0.5 m的单摆的周期是0.707 s
B.摆长是0.5 m的单摆的周期是1 s
C.周期是1 s的单摆的摆长为2 m
D.周期是4 s的单摆的摆长为4 m
3.[多选]如图所示,A,B分别为单摆做简谐运动时摆球的不同位置。其中A处为单摆摆动的最高位置,虚线为过悬点的竖直线。以单摆最低位置为重力势能零点,则单摆在摆动过程中 ( )
A.位于B处时动能最大
B.位于A处时势能最大
C.在A处的势能大于在B处的动能
D.在B处的机械能大于在A处的机械能
4.某一单摆原来的周期是2 s,在下列情况下,周期有无变化?如有变化,变为多少?
(1)摆长减为原长的。
(2)摆球的质量减为原来的。
(3)振幅减为原来的。
(4)重力加速度减为原来的。
5.已知单摆的摆长是1 m时,摆动周期是2 s。当摆长改变为0.81 m时,摆动周期是多少?要使摆动周期为4 s,摆长应是多少?
6.如图所示,光滑圆槽的半径R远大于小球运动的弧长。甲、乙、丙三个小球(均可视为质点)同时由静止释放,开始时,甲球比乙球离槽最低点O远些,丙球在槽的圆心处。请比较它们第一次到达点O的先后顺序,并说明理由。
7.某单摆及其振动图像如图所示。
(1)若取从E指向G为正方向,α为最大摆角,则图像中点O、A、B、C、D分别对应单摆中的哪个位置?一个周期内回复力为正且减小、并与速度同方向的时间范围是多少?势能增加且速度为正的时间范围是多少?
(2)单摆摆球多次通过位置E时,哪些相关物理量发生了变化?
(3)单摆的摆长是多少?(取重力加速度g=
10 m/s2,π2=10)
8.某同学用单摆测定一座山的海拔,在山顶上他测得摆长为l的单摆做简谐运动的周期为T。已知引力常量为G,地球质量为M,地球半径为R。求山顶的海拔。
9.一单摆在地面处的摆动周期与其在某矿井底部的摆动周期的比值为k。设地球的半径为R并假定其密度均匀,已知质量均匀分布的球壳对壳内物体的引力为0,求矿井的深度d。
13.将一测力传感器连接到计算机上就可以测量快速变化的力,如图(a)所示点O为单摆的悬点,将传感器接在摆线与点O之间,现将小球(可视为质点)拉到点A,此时细线处于张紧状态,释放摆球,则摆球在竖直平面内的ABC之间来回摆动,其中点B为运动最低位置,∠AOB=∠COB=α,α小于5°且是未知量。如图(b)所示是由计算得到细线对摆球的拉力大小F随时间变化的图像,且图中t=0时刻为摆球从点A开始运动的时刻,据力学规律和题中信息(g取10 m/s2),求:
(1)单摆的周期和摆长。
(2)摆球的质量及摆动过程中的最大速度。
第4节 单摆
参考答案
BD
D
BC
解:由单摆周期公式T=知,单摆的周期与摆球质量和振幅无关,故(2)(3)两种情况,周期不变。
(1)中,由周期公式得T1==1 s。
(4)中,由周期公式得T2=2T=4 s。
解:由单摆周期公式T=得, =,则T′=0.9T=1.8 s,由单摆周期公式T=得, =,则L″=4L=4 m。
解:甲、乙两球沿光滑圆槽做简谐运动,等效摆长为R,周期相同,甲、乙两球同时到达点O,需要的时间t1===,
丙球做自由落体运动,由R=,得t2==·,
,即t1>t2,故丙球最先到达点O,甲、乙两球同时到达点O。
解:(1)单摆的小角度摆动是简谐运动,从振动图像看出:
O点对应平衡位置,对应单摆中的E点;
A点位于正向最大位移处,对应单摆中的G点;
B点位于平衡位置,对应单摆中的E点;
C点位于负向最大位移处,对应单摆中的F点;
D点位于平衡位置,对应单摆中的E点。
由题图可知,单摆的周期为2 s,F回为正且减小,应该位于平衡位置左侧且正衡位置,即由F→E运动,对应时间范围应为1.5~2.0 s。
势能增加且速度为正的时间范围为0~0.5 s。
(2)摆球多次通过同一位置E时,位移是相同的,为0,摆线弹力相同,回复力(加速度)相同,速度大小相等,动能是相同的,但速度方向不同,故动量不同。
即速度、动量发生了变化。
(3)由T=,得l===1 m。
解:设山顶上的重力加速度为g′,则有T=,得出g′= ①
设山顶的海拔为h,则有mg′= ②
联立①②式解得h=。
解:在地面上有mg=,M=πρR3,解得g=πGρR
单摆的周期T=2π
在矿井底部单摆的周期T′=,
此处mg′=,半径为R-d的地球对应的质量M′=,解得g′=,
,,即=k2,得出d=(1-k2)R。
解:(1)由图(b)可知,周期T=0.4π s,由单摆周期公式T=得L== m=0.4 m。
(2) 在最高点A,有Fmin=mgcos α=0.495 N,在最低点B,有Fmax-mg=,从A到B,机械能守恒,有mgL(1-cos α)=,联立得m=0.05 kg,v≈0.283 m/s。
