21.1 一元二次方程 课件(共22张PPT)
文档属性
| 名称 | 21.1 一元二次方程 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-08 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
人教版九年级上册
21.1 一元二次方程
3.了解一元二次方程的根的概念,会检验一个数是不是一元二次方程的根.
1.理解一元二次方程的概念,会判断一个方程是不是一元二次方程.
2.会将一元二次方程化为一般形式,知道各项的名称.
学习目标
判断下列式子是不是一元一次方程:
一元一次方程
1.只含有一个未知数;
2.未知数的次数都是1;
3.等号两边都是整式.
知识回顾
设雕像下部高x m,可得方程:
解:雕像上部的高度AC,下部的高度BC应有如下关系:
问题1 在设计人体雕像时,使雕像的上部(腰以上)与下部(腰以下)的高度比,等于下部与全部(全身)的高度比,可以增加视觉美感. 按此比例,要设计一座2 m高的人体雕像,那么雕像的下部应设计为多高?
A
C
B
2
x
x2=2(2 x),
即 .
课堂导入
整理得 .
x2+2x 4=0
①
由方程①可得雕像的下部应设计的高度.
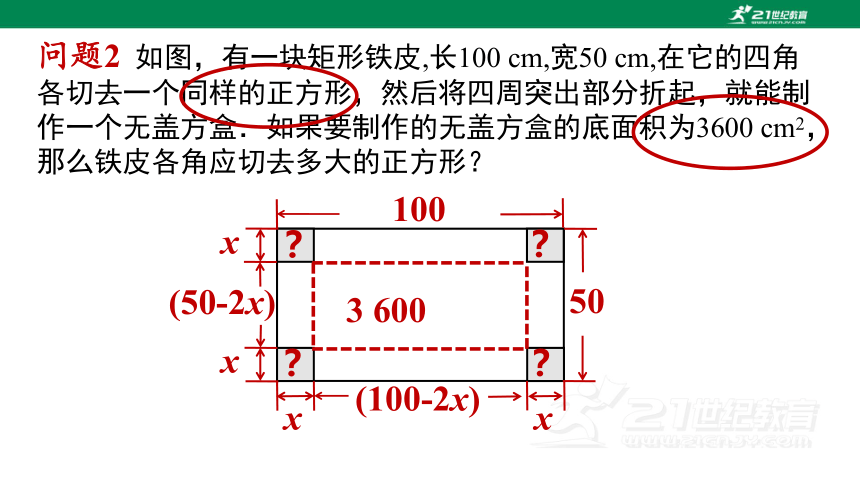
问题2 如图,有一块矩形铁皮,长100 cm,宽50 cm,在它的四角各切去一个同样的正方形,然后将四周突出部分折起,就能制作一个无盖方盒.如果要制作的无盖方盒的底面积为3600 cm2,那么铁皮各角应切去多大的正方形?
3 600
100
50
x
x
(100-2x)
x
x
(50-2x)
?
?
?
?
解:设切去的正方形的边长为x cm,
则盒底的长为(100 2x) cm,
宽为(50 2x) cm.
根据方盒的底面积为3 600 cm2,
得:
(100 2x)(50 2x)=3 600.
整理,得 4x2 300x+1 400=0.
化简,得 x2 75x+350=0 .②
由方程②可以得出所切正方形的具体尺寸.
50
x
3 600
100
x
x
(100-2x)
x
(50-2x)
问题3 要组织一次排球邀请赛,参赛的每两个队之间都要比赛一场.根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛,比赛组织者应邀请多少个队参赛?
解:全部比赛的场数为4×7=28.
设应邀请x个队参赛,每个队要与其他(x-1)个队各赛一场,因为甲队对乙队的比赛和乙队对甲队的比赛是同一场比赛,所以全部比赛共有 场.
列方程 x(x 1)=28 ,
整理,得 x x=28 ,
化简,得x x=56 .③ 由方程③可以得出参赛队数.
1.这些方程的等号两边都是整式;
2.方程中只含有一个未知数,未知数的最高次数是2.
③x2 x=56
②x2 75x+350=0
①x2+2x 4=0
观察由上面的问题得到的方程有什么特点?
像这样,等号两边都是整式,只含有一个未知数(一元),并且未知数的最高次数是2(二次)的方程,叫做一元二次方程.
知识点1
新知探究
知识点2
新知探究
一般地,任何一个关于 x 的一元二次方程,经过整理,都能化成如下形式:ax2 + bx +c = 0(a≠0)
这种形式叫做一元二次方程的一般形式.其中 ax 2 是二次项,a 是二次项系数;bx是一次项,b 是一次项系数;c 是常数项.
为什么要规定a≠0呢?b,c呢?
a=0,二次项为0,就不是二次了,b,c可以取任意数.
注意:指出方程各项的系数时要带上前面的符号.
跟踪训练
新知探究
例1 判断下列关于x的方程是不是一元二次方程.
符合一元二次方程的概念.
含有两个未知数,不是一元.
不是整式方程.
a的取值不确定,若a=0,则不是一元二次方程.
(1)
(2)
(3)
(4)
例2 若方程 (m+2)x|m| 3mx+1=0 是关于x 的一元二次方程,则 ( )
A.m≠±2 B.m=2
C.m= 2 D.m=±2
B
解:
一元二次方程的概念
m+2≠0
未知数的最高次数是2
二次项系数不为0
m=2
|m|=2
化一般式的步骤:去分母→去括号→移项(等号右边0)→合并同类项→确定a,b,c(注意带前面的符号).
例3 把下列方程化成一元二次方程的一般形式,并写出它们的二次项系数、一次项系数和常数项.
a=1,b=-3,c=-4.
a=2 ,b=-3,c= -9.
a=2,b=2,c=-25.
知识点3
新知探究
使方程左右两边相等的未知数的值就是这个一元二次方程的解,一元二次方程的解也叫做一元二次方程的根.
判断一个数是不是一元二次方程的根的方法:将这个数代入一元二次方程的左右两边,看是否相等,若相等,则该数是这个方程的根;若不相等,则该数不是这个方程的根.
跟踪训练
新知探究
例4 下列哪些数是一元二次方程 x2-4x+3=0 的解?
-1, 0, 1, 3.
1. 已知关于x的方程(a2-1)x2+(a+1)x=2.
(1)当a取何值时,此方程为一元一次方程?
(2)当a取何值时,此方程为一元二次方程?
随堂练习
解: 将原方程化成一般式为:(a2-1)x2+(a+1)x-2=0
(1)要使原方程为一元一次方程,则需
解得a=1.
(2)要使原方程为一元二次方程,则需a2-1≠0,即a≠±1.
2.根据下列问题列方程,并将所列方程化成一元二次方程的一般形式:
(1)一个圆的面积是 6.28 cm2,求半径;
(2)一个直角三角形的两条直角边相差 3 cm,面积是 9 cm2,求较长的直角边.
解:(1)设圆的半径为 x cm,根据题意,得πx2=6.28,
化为一般形式为 πx2-6.28=0.
(2)设较长直角边的长为 x cm,则较短直角边的长为 (x-3) cm,
根据题意,得 x(x-3)=9,
化为一般形式为 x2-3x-18=0.
3.若 2n(n≠0) 是关于 x 的方程 x2-2mx+2n=0 的根,则 m-n 的值为 .
解: ∵ 2n(n≠0) 是关于 x 的方程 x2-2mx+2n=0 的根,
∴ (2n)2-2m×2n+2n=0,
∴2n(2n-2m+1)=0,
∵n≠0,
∴2n-2m+1=0,
化简得m-n= .
一元二次方程
ax2+bx+c=0(a≠0)
只含有一个未知数
未知数的最高次数是2
是整式方程
一元二次方程的一般形式
一元二次方程的解(根)
一元二次方程的概念
课堂小结
1.(2020 枣庄中考)已知关于x的一元二次方程(a-1)x2-2x+a2-1=0有一个根为x=0,则a= .
解: 把x=0代入(a-1)x2-2x+a2-1=0,
得a2-1=0,解得a=±1.
∵(a-1)x2-2x+a2-1=0是关于x的一元二次方程,
∴a-1≠0,
∴a=-1.
对接中考
-1
2.如图,有一张矩形纸片,长10 cm,宽 6 cm,在它的四角各剪去一个同样的小正方形,然后折叠成一个无盖的长方体纸盒.若纸盒的底面面积是 32 cm2,求剪去的小正方形的边长.设剪去的小正方形的边长是 x cm,根据题意可列方程为( )
A.10×6-4×6x=32
B.(10-2x)(6-2x)=32
C.(10-x)(6-x)=32
D.10×6-4x2=32
B
类似例题的素养解读见《教材帮》RJ九上21.1节中考帮
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版九年级上册
21.1 一元二次方程
3.了解一元二次方程的根的概念,会检验一个数是不是一元二次方程的根.
1.理解一元二次方程的概念,会判断一个方程是不是一元二次方程.
2.会将一元二次方程化为一般形式,知道各项的名称.
学习目标
判断下列式子是不是一元一次方程:
一元一次方程
1.只含有一个未知数;
2.未知数的次数都是1;
3.等号两边都是整式.
知识回顾
设雕像下部高x m,可得方程:
解:雕像上部的高度AC,下部的高度BC应有如下关系:
问题1 在设计人体雕像时,使雕像的上部(腰以上)与下部(腰以下)的高度比,等于下部与全部(全身)的高度比,可以增加视觉美感. 按此比例,要设计一座2 m高的人体雕像,那么雕像的下部应设计为多高?
A
C
B
2
x
x2=2(2 x),
即 .
课堂导入
整理得 .
x2+2x 4=0
①
由方程①可得雕像的下部应设计的高度.
问题2 如图,有一块矩形铁皮,长100 cm,宽50 cm,在它的四角各切去一个同样的正方形,然后将四周突出部分折起,就能制作一个无盖方盒.如果要制作的无盖方盒的底面积为3600 cm2,那么铁皮各角应切去多大的正方形?
3 600
100
50
x
x
(100-2x)
x
x
(50-2x)
?
?
?
?
解:设切去的正方形的边长为x cm,
则盒底的长为(100 2x) cm,
宽为(50 2x) cm.
根据方盒的底面积为3 600 cm2,
得:
(100 2x)(50 2x)=3 600.
整理,得 4x2 300x+1 400=0.
化简,得 x2 75x+350=0 .②
由方程②可以得出所切正方形的具体尺寸.
50
x
3 600
100
x
x
(100-2x)
x
(50-2x)
问题3 要组织一次排球邀请赛,参赛的每两个队之间都要比赛一场.根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛,比赛组织者应邀请多少个队参赛?
解:全部比赛的场数为4×7=28.
设应邀请x个队参赛,每个队要与其他(x-1)个队各赛一场,因为甲队对乙队的比赛和乙队对甲队的比赛是同一场比赛,所以全部比赛共有 场.
列方程 x(x 1)=28 ,
整理,得 x x=28 ,
化简,得x x=56 .③ 由方程③可以得出参赛队数.
1.这些方程的等号两边都是整式;
2.方程中只含有一个未知数,未知数的最高次数是2.
③x2 x=56
②x2 75x+350=0
①x2+2x 4=0
观察由上面的问题得到的方程有什么特点?
像这样,等号两边都是整式,只含有一个未知数(一元),并且未知数的最高次数是2(二次)的方程,叫做一元二次方程.
知识点1
新知探究
知识点2
新知探究
一般地,任何一个关于 x 的一元二次方程,经过整理,都能化成如下形式:ax2 + bx +c = 0(a≠0)
这种形式叫做一元二次方程的一般形式.其中 ax 2 是二次项,a 是二次项系数;bx是一次项,b 是一次项系数;c 是常数项.
为什么要规定a≠0呢?b,c呢?
a=0,二次项为0,就不是二次了,b,c可以取任意数.
注意:指出方程各项的系数时要带上前面的符号.
跟踪训练
新知探究
例1 判断下列关于x的方程是不是一元二次方程.
符合一元二次方程的概念.
含有两个未知数,不是一元.
不是整式方程.
a的取值不确定,若a=0,则不是一元二次方程.
(1)
(2)
(3)
(4)
例2 若方程 (m+2)x|m| 3mx+1=0 是关于x 的一元二次方程,则 ( )
A.m≠±2 B.m=2
C.m= 2 D.m=±2
B
解:
一元二次方程的概念
m+2≠0
未知数的最高次数是2
二次项系数不为0
m=2
|m|=2
化一般式的步骤:去分母→去括号→移项(等号右边0)→合并同类项→确定a,b,c(注意带前面的符号).
例3 把下列方程化成一元二次方程的一般形式,并写出它们的二次项系数、一次项系数和常数项.
a=1,b=-3,c=-4.
a=2 ,b=-3,c= -9.
a=2,b=2,c=-25.
知识点3
新知探究
使方程左右两边相等的未知数的值就是这个一元二次方程的解,一元二次方程的解也叫做一元二次方程的根.
判断一个数是不是一元二次方程的根的方法:将这个数代入一元二次方程的左右两边,看是否相等,若相等,则该数是这个方程的根;若不相等,则该数不是这个方程的根.
跟踪训练
新知探究
例4 下列哪些数是一元二次方程 x2-4x+3=0 的解?
-1, 0, 1, 3.
1. 已知关于x的方程(a2-1)x2+(a+1)x=2.
(1)当a取何值时,此方程为一元一次方程?
(2)当a取何值时,此方程为一元二次方程?
随堂练习
解: 将原方程化成一般式为:(a2-1)x2+(a+1)x-2=0
(1)要使原方程为一元一次方程,则需
解得a=1.
(2)要使原方程为一元二次方程,则需a2-1≠0,即a≠±1.
2.根据下列问题列方程,并将所列方程化成一元二次方程的一般形式:
(1)一个圆的面积是 6.28 cm2,求半径;
(2)一个直角三角形的两条直角边相差 3 cm,面积是 9 cm2,求较长的直角边.
解:(1)设圆的半径为 x cm,根据题意,得πx2=6.28,
化为一般形式为 πx2-6.28=0.
(2)设较长直角边的长为 x cm,则较短直角边的长为 (x-3) cm,
根据题意,得 x(x-3)=9,
化为一般形式为 x2-3x-18=0.
3.若 2n(n≠0) 是关于 x 的方程 x2-2mx+2n=0 的根,则 m-n 的值为 .
解: ∵ 2n(n≠0) 是关于 x 的方程 x2-2mx+2n=0 的根,
∴ (2n)2-2m×2n+2n=0,
∴2n(2n-2m+1)=0,
∵n≠0,
∴2n-2m+1=0,
化简得m-n= .
一元二次方程
ax2+bx+c=0(a≠0)
只含有一个未知数
未知数的最高次数是2
是整式方程
一元二次方程的一般形式
一元二次方程的解(根)
一元二次方程的概念
课堂小结
1.(2020 枣庄中考)已知关于x的一元二次方程(a-1)x2-2x+a2-1=0有一个根为x=0,则a= .
解: 把x=0代入(a-1)x2-2x+a2-1=0,
得a2-1=0,解得a=±1.
∵(a-1)x2-2x+a2-1=0是关于x的一元二次方程,
∴a-1≠0,
∴a=-1.
对接中考
-1
2.如图,有一张矩形纸片,长10 cm,宽 6 cm,在它的四角各剪去一个同样的小正方形,然后折叠成一个无盖的长方体纸盒.若纸盒的底面面积是 32 cm2,求剪去的小正方形的边长.设剪去的小正方形的边长是 x cm,根据题意可列方程为( )
A.10×6-4×6x=32
B.(10-2x)(6-2x)=32
C.(10-x)(6-x)=32
D.10×6-4x2=32
B
类似例题的素养解读见《教材帮》RJ九上21.1节中考帮
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
