14.2三角形全等的判定 (5) 课件(共25张PPT)
文档属性
| 名称 | 14.2三角形全等的判定 (5) 课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-08 00:00:00 | ||
图片预览








文档简介
(共25张PPT)
沪科版 八年级上册
14.2三角形全等的判定 (5)
全等三角形判定方法的综合应用
教学目标
1.掌握全等三角形的判定方法.
2.能用全等三角形证明三角形中的边或角相等.
教学重点:
教学难点:
用全等三角形证明边或角相等.
规范叙述证明三角形全等的过程.
全等三角形的判定方法
SSS
SAS
ASA
AAS
判定两个三角形全等的条件中
至少有一组边对应相等.
结论:
全等判定三条件,总得有边方实现.
三边对等最易找,两边一角需夹角.
两角一边任意边,角边角或角角边..
复习旧知
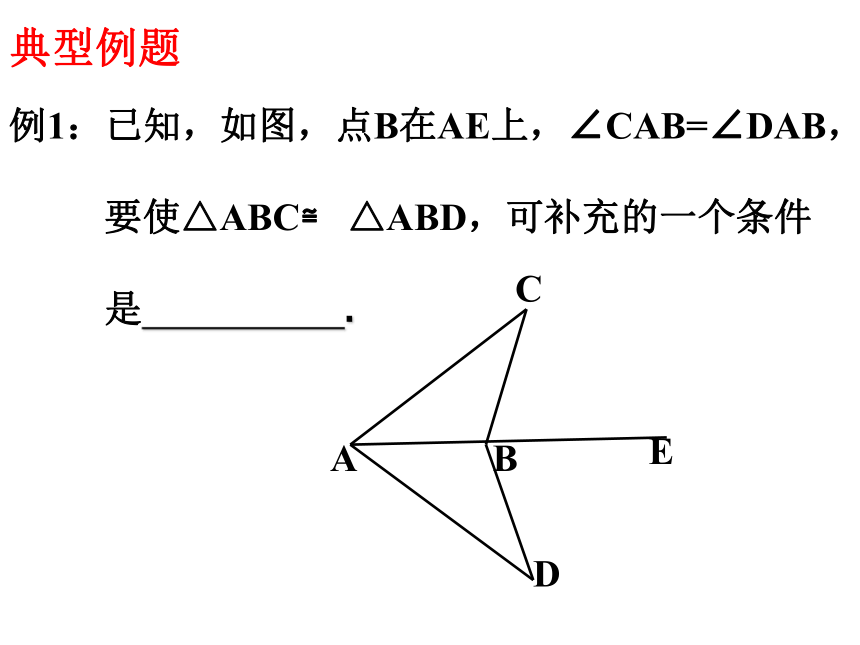
例1:已知,如图,点B在AE上,∠CAB=∠DAB,
要使△ABC≌ △ABD,可补充的一个条件
是 .
典型例题
A
B
C
D
E
例1:已知,如图,点B在AE
上,∠CAB=∠DAB,要使
ΔABC≌ΔABD,可补充的
一个条件是 .
分析:现在我们已知
②用ASA,需要补充条件
④此外,补充条件
SAS
ASA
AAS
A→∠CAB=∠DAB
S→ AB=AB(公共边) .
典型例题
AD=AC,
∠CBA=∠DBA,
∠C=∠D,
∠CBE=∠DBE也可以.
AD=AC
∠CBA=∠DBA
∠C=∠D
∠CBE=∠DBE
③用AAS,需要补充条件
①用SAS,需要补充条件
A
B
C
D
E
已知,如图,AE=AD,要使△ABD≌△ACE,
请你增加一个条件是 .
AB=AC,
∠B=∠C,
∠BDA =∠CEA,
∠CDB=∠BEC,
练习巩固
A
B
C
D
E
证明三角形全等或三角形中的边角相等,有时需要证明两次三角形全等才能完成,用到证明三角形全等的方法可能也不止一种.
学习新知
要学会分析法寻找思路.
例8:已知:如图AB=CD,BC=DA,E、F是AC上的两点,且AE=CF.求证:BF=DE.
A
B
C
D
E
F
2
1
要证:
△BCF≌△DAE
∠1=∠2
BF=DE
△ABC≌△CDA
典型例析
例8:已知:如图AB=CD,BC=DA,E、F是AC上的两点,且AE=CF.求证:BF=DE.
A
B
C
D
E
F
2
1
证明:在△ABC和△CDA中
AB=CD
BC=DA
CA=AC
(已知)
(已知)
(公共边)
∴ △ABC≌△CDA
(SSS)
∴ ∠1=∠2
(全等三角形的对应角相等)
A
B
C
D
E
F
2
1
证明:在△ABC和△CDA中
AB=CD
BC=DA
CA=AC
(已知)
(已知)
(公共边)
∴ △ABC≌△CDA
(SSS)
∴ ∠1=∠2
(全等三角形的对应角相等)
在△BCF和△DAE中
BC=DA
∠1=∠2
CF=AE
(已知)
(已证)
(已知)
∴ △BCF≌△DAE
(SAS)
∴ BF=DE
(全等三角形的对应边相等)
想一想:还有别的证法吗?
如图,已知:AB=CD,AC=DB,BE=CE.
A
B
C
E
D
求证:AE=DE.
要证:
△ABE≌△DEC
∠ABE=∠DCE
AE=DE
△ABC≌△DCB
练习巩固
如图,已知:AB=CD,AC=DB,BE=CE.
求证:AE=DE.
A
B
C
E
D
在△ABC和△DCB中,
AB=CD
AC=DB
∴ △ABC≌△DCB
∴ ∠ABC=∠DCB.
BC=CB
证明:
(SSS)
A
B
C
E
D
在△ABC和△DCB中,
AB=CD
AC=DB
∴ △ABC≌△DCB
∴ ∠ABC=∠DCB.
BC=CB
在△ABE和△CDE中,
AB=DC
∠ABE=∠DCE
∴ △ABE≌△DCE
∴AE=DE.
BE=CE
证明:
(SSS)
(SAS)
文字叙述形式命题的证明.
对于文字叙述形式的命题,要先根据题意画出图形,再结合题意和所画图形写出已知、求证,然后进行证明.
学习新知
求证:全等三角形的对应边上的高相等.
分析:先根据题意画出图形,再结合题意和所画图形写出已知、求证,然后进行证明.
已知: 如图,△ABC≌△A′B′C′,AD,A′D′分别是 △ABC和△A′B′C′的高.
∟
D
B
C
A
∟
D′
B′
C′
A′
求证:AD=A′D′.
典型例析
已知: 如图△ABC≌△A′B′C′,AD,A′D′分别是 △ABC和△A′B′C′的高,求证:AD=A′D′.
∟
B′
C′
D′
A′
∟
B
C
D
A
证明:
∵△ABC≌△A′B′C′,
∴∠B=∠B′,
AB=A′B′.
∵AD⊥BC,A′D′⊥B′C′ ,
∴∠ADB=∠A′D′B′.
∠ADB=∠A′D′B′
∠B=∠B′
在△ABD≌△A′B′D′中
AB=A′ B′.
∴△ABD≌△A′B′D′
∴AD=A′D′.
(全等三角形对应边相等).
(AAS)
1.求证:全等三角形的对应边上的中线相等.
学以致用
2.求证:全等三角形的对应角的平分线线相等.
1.已知: 如图△ABC≌△A′B′C′,AD,A′D′分别是 △ABC和△A′B′C′的中线,求证:AD=A′D′.
B′
C′
D′
A′
B
C
D
A
证明:
∵△ABC≌△A′B′C′,
∴AB= A′B′ ,
BC=B′ C′.
∵BD= BC,B′D′= B′C′ ,
∴DB=D′B′
DB=D′B′
∴△ABD≌△A′B′D′
∴AD=A′ D′.
(全等三角形对应边相等).
∠B=∠B′
在△ABD≌△A′B′D′中
AB=A′ B′.
∠B=∠B′ ,
1
2
1
2
(SAS)
2.已知: 如图△ABC≌△A′B′C′,AD,A′D′分别是△ABC和△A′B′C′的角平分线,求证:AD=A′D′.
B′
C′
D′
A′
B
C
D
A
证明:
∵△ABC≌△A′B′C′,
∴AB= A′B′ ,
∠BAC=∠B′A′C′.
∵∠1= ∠BAC,
∴∠1=∠2.
∠1=∠2
∴△ABD≌△A′B′D′
∴AD=A′ D′.
(全等三角形对应边相等).
∠B=∠B′
在△ABD≌△A′B′D′中
AB=A′B′.
∠B=∠B′ ,
1
2
1
2
∠2= ∠B′A′C′ ,
1
2
(ASA)
全等三角形的对应边上的高相等.
全等三角形的对应边上的中线相等.
全等三角形的对应角的平分线相等.
全等三角形的对应边相等.
全等三角形的对应角相等.
全等三角形的性质:
课堂小结
如图,已知,在△ABC中,BD,CE分别是
AC,AB边的中线,延长BD至F,使DF=BD,
延长CE至G使EG=CE,连接AF,AG.
求证:AF=AG.
巩固提高
A
B
C
D
E
F
G
A
B
C
D
E
F
G
∴ AD=CD.
证明:
∵BD是AC的中线,
在△AFD和△CBD中,
AD=CD
FD=BD
∴ △AFD≌△CBD
∴AF=BC.
(SAS)
∠ADF=∠CDB
∴ AE=BE.
∵CE是AB的中线,
在△AGE和△BCE中,
AE=BE
GE=CE
∴ △AGE≌△BCE
∴AG=BC.
(SAS)
∠AEG=∠BEC
∴AF=AG.
今天作业
课本P113页第11、12题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 八年级上册
14.2三角形全等的判定 (5)
全等三角形判定方法的综合应用
教学目标
1.掌握全等三角形的判定方法.
2.能用全等三角形证明三角形中的边或角相等.
教学重点:
教学难点:
用全等三角形证明边或角相等.
规范叙述证明三角形全等的过程.
全等三角形的判定方法
SSS
SAS
ASA
AAS
判定两个三角形全等的条件中
至少有一组边对应相等.
结论:
全等判定三条件,总得有边方实现.
三边对等最易找,两边一角需夹角.
两角一边任意边,角边角或角角边..
复习旧知
例1:已知,如图,点B在AE上,∠CAB=∠DAB,
要使△ABC≌ △ABD,可补充的一个条件
是 .
典型例题
A
B
C
D
E
例1:已知,如图,点B在AE
上,∠CAB=∠DAB,要使
ΔABC≌ΔABD,可补充的
一个条件是 .
分析:现在我们已知
②用ASA,需要补充条件
④此外,补充条件
SAS
ASA
AAS
A→∠CAB=∠DAB
S→ AB=AB(公共边) .
典型例题
AD=AC,
∠CBA=∠DBA,
∠C=∠D,
∠CBE=∠DBE也可以.
AD=AC
∠CBA=∠DBA
∠C=∠D
∠CBE=∠DBE
③用AAS,需要补充条件
①用SAS,需要补充条件
A
B
C
D
E
已知,如图,AE=AD,要使△ABD≌△ACE,
请你增加一个条件是 .
AB=AC,
∠B=∠C,
∠BDA =∠CEA,
∠CDB=∠BEC,
练习巩固
A
B
C
D
E
证明三角形全等或三角形中的边角相等,有时需要证明两次三角形全等才能完成,用到证明三角形全等的方法可能也不止一种.
学习新知
要学会分析法寻找思路.
例8:已知:如图AB=CD,BC=DA,E、F是AC上的两点,且AE=CF.求证:BF=DE.
A
B
C
D
E
F
2
1
要证:
△BCF≌△DAE
∠1=∠2
BF=DE
△ABC≌△CDA
典型例析
例8:已知:如图AB=CD,BC=DA,E、F是AC上的两点,且AE=CF.求证:BF=DE.
A
B
C
D
E
F
2
1
证明:在△ABC和△CDA中
AB=CD
BC=DA
CA=AC
(已知)
(已知)
(公共边)
∴ △ABC≌△CDA
(SSS)
∴ ∠1=∠2
(全等三角形的对应角相等)
A
B
C
D
E
F
2
1
证明:在△ABC和△CDA中
AB=CD
BC=DA
CA=AC
(已知)
(已知)
(公共边)
∴ △ABC≌△CDA
(SSS)
∴ ∠1=∠2
(全等三角形的对应角相等)
在△BCF和△DAE中
BC=DA
∠1=∠2
CF=AE
(已知)
(已证)
(已知)
∴ △BCF≌△DAE
(SAS)
∴ BF=DE
(全等三角形的对应边相等)
想一想:还有别的证法吗?
如图,已知:AB=CD,AC=DB,BE=CE.
A
B
C
E
D
求证:AE=DE.
要证:
△ABE≌△DEC
∠ABE=∠DCE
AE=DE
△ABC≌△DCB
练习巩固
如图,已知:AB=CD,AC=DB,BE=CE.
求证:AE=DE.
A
B
C
E
D
在△ABC和△DCB中,
AB=CD
AC=DB
∴ △ABC≌△DCB
∴ ∠ABC=∠DCB.
BC=CB
证明:
(SSS)
A
B
C
E
D
在△ABC和△DCB中,
AB=CD
AC=DB
∴ △ABC≌△DCB
∴ ∠ABC=∠DCB.
BC=CB
在△ABE和△CDE中,
AB=DC
∠ABE=∠DCE
∴ △ABE≌△DCE
∴AE=DE.
BE=CE
证明:
(SSS)
(SAS)
文字叙述形式命题的证明.
对于文字叙述形式的命题,要先根据题意画出图形,再结合题意和所画图形写出已知、求证,然后进行证明.
学习新知
求证:全等三角形的对应边上的高相等.
分析:先根据题意画出图形,再结合题意和所画图形写出已知、求证,然后进行证明.
已知: 如图,△ABC≌△A′B′C′,AD,A′D′分别是 △ABC和△A′B′C′的高.
∟
D
B
C
A
∟
D′
B′
C′
A′
求证:AD=A′D′.
典型例析
已知: 如图△ABC≌△A′B′C′,AD,A′D′分别是 △ABC和△A′B′C′的高,求证:AD=A′D′.
∟
B′
C′
D′
A′
∟
B
C
D
A
证明:
∵△ABC≌△A′B′C′,
∴∠B=∠B′,
AB=A′B′.
∵AD⊥BC,A′D′⊥B′C′ ,
∴∠ADB=∠A′D′B′.
∠ADB=∠A′D′B′
∠B=∠B′
在△ABD≌△A′B′D′中
AB=A′ B′.
∴△ABD≌△A′B′D′
∴AD=A′D′.
(全等三角形对应边相等).
(AAS)
1.求证:全等三角形的对应边上的中线相等.
学以致用
2.求证:全等三角形的对应角的平分线线相等.
1.已知: 如图△ABC≌△A′B′C′,AD,A′D′分别是 △ABC和△A′B′C′的中线,求证:AD=A′D′.
B′
C′
D′
A′
B
C
D
A
证明:
∵△ABC≌△A′B′C′,
∴AB= A′B′ ,
BC=B′ C′.
∵BD= BC,B′D′= B′C′ ,
∴DB=D′B′
DB=D′B′
∴△ABD≌△A′B′D′
∴AD=A′ D′.
(全等三角形对应边相等).
∠B=∠B′
在△ABD≌△A′B′D′中
AB=A′ B′.
∠B=∠B′ ,
1
2
1
2
(SAS)
2.已知: 如图△ABC≌△A′B′C′,AD,A′D′分别是△ABC和△A′B′C′的角平分线,求证:AD=A′D′.
B′
C′
D′
A′
B
C
D
A
证明:
∵△ABC≌△A′B′C′,
∴AB= A′B′ ,
∠BAC=∠B′A′C′.
∵∠1= ∠BAC,
∴∠1=∠2.
∠1=∠2
∴△ABD≌△A′B′D′
∴AD=A′ D′.
(全等三角形对应边相等).
∠B=∠B′
在△ABD≌△A′B′D′中
AB=A′B′.
∠B=∠B′ ,
1
2
1
2
∠2= ∠B′A′C′ ,
1
2
(ASA)
全等三角形的对应边上的高相等.
全等三角形的对应边上的中线相等.
全等三角形的对应角的平分线相等.
全等三角形的对应边相等.
全等三角形的对应角相等.
全等三角形的性质:
课堂小结
如图,已知,在△ABC中,BD,CE分别是
AC,AB边的中线,延长BD至F,使DF=BD,
延长CE至G使EG=CE,连接AF,AG.
求证:AF=AG.
巩固提高
A
B
C
D
E
F
G
A
B
C
D
E
F
G
∴ AD=CD.
证明:
∵BD是AC的中线,
在△AFD和△CBD中,
AD=CD
FD=BD
∴ △AFD≌△CBD
∴AF=BC.
(SAS)
∠ADF=∠CDB
∴ AE=BE.
∵CE是AB的中线,
在△AGE和△BCE中,
AE=BE
GE=CE
∴ △AGE≌△BCE
∴AG=BC.
(SAS)
∠AEG=∠BEC
∴AF=AG.
今天作业
课本P113页第11、12题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
