14.1 全等三角形 课件(共25张PPT)
文档属性
| 名称 | 14.1 全等三角形 课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-08 00:00:00 | ||
图片预览



文档简介
(共25张PPT)
沪科版 八年级上册
14.1 全等三角形
教学目标
1.知道全等形,全等三角形的概念
2.知道全等三角形的性质
3.能识别全等三角形的对应边、对应角
教学重点:
识别全等三角形的对应边、对应角
教学难点:
识别全等三角形的对应边、对应角
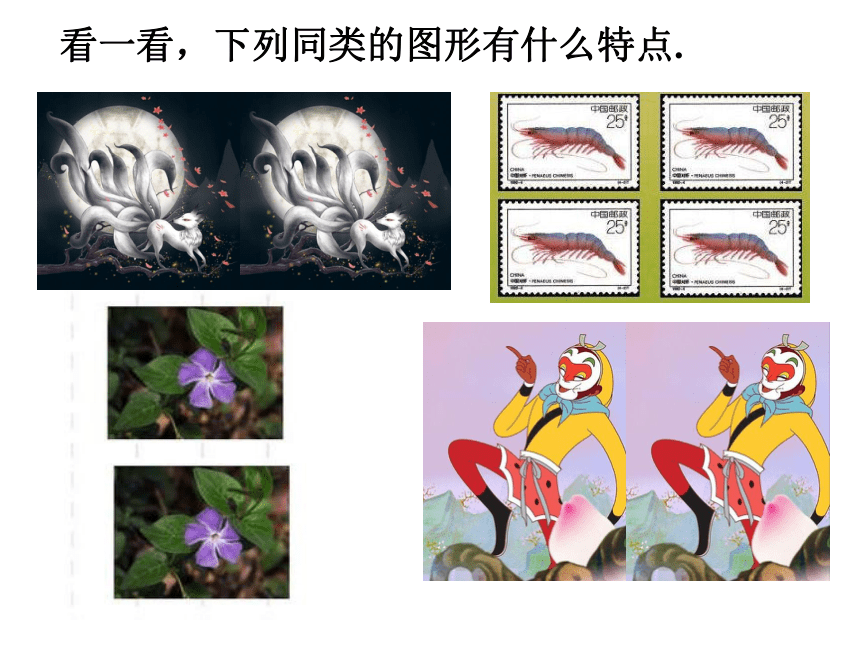
看一看,下列同类的图形有什么特点.
能够完全重合的两个图形称为全等形.
1.全等形的定义
能够完全重合的两个三角形称为全等三角形.
2.全等三角形的定义
A
B
C
D
E
F
学习新知
A
B
C
D
E
F
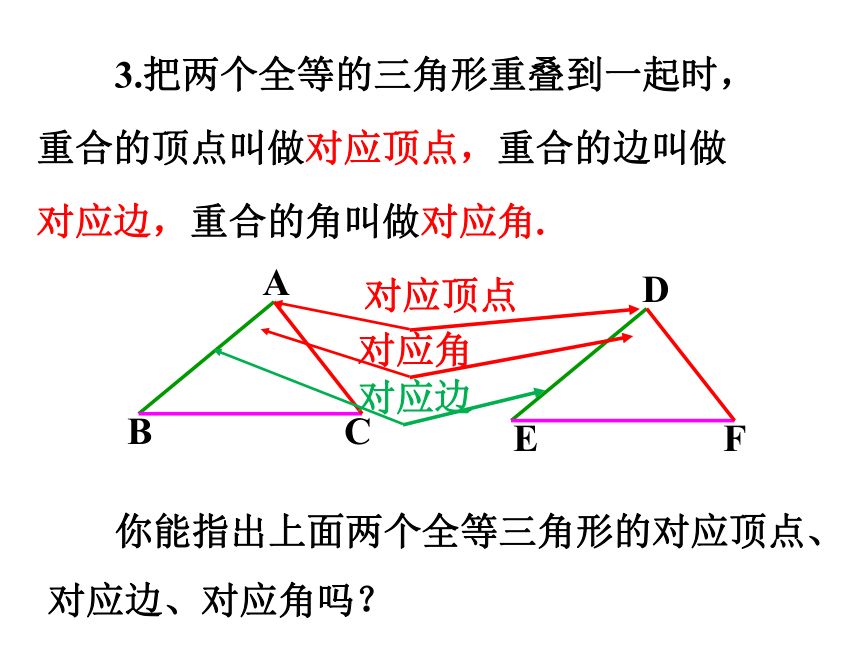
3.把两个全等的三角形重叠到一起时,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角.
你能指出上面两个全等三角形的对应顶点、
对应边、对应角吗?
对应顶点
对应角
对应边
N
M
S
O
T
D
C
O
A
B
A
B
C
D
E
F
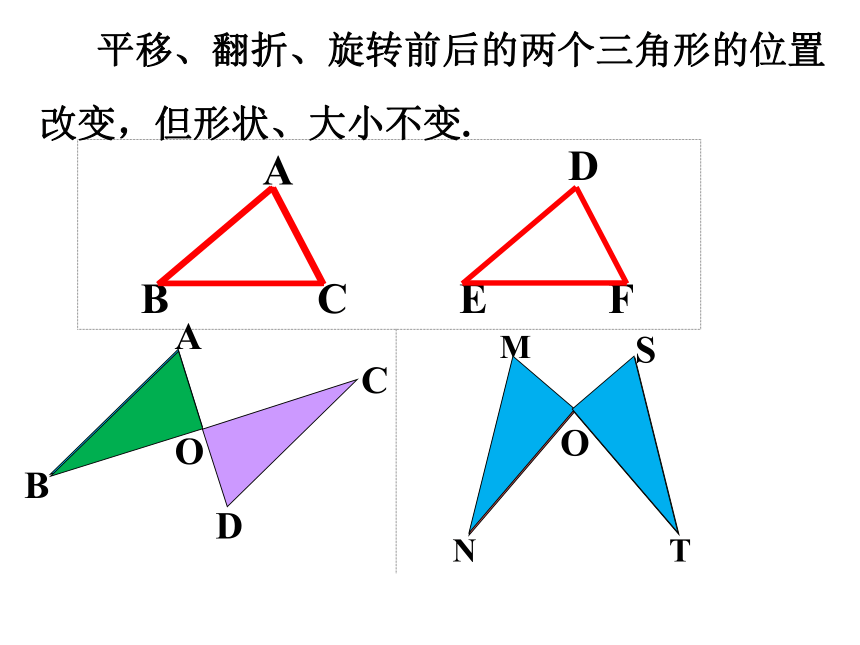
平移、翻折、旋转前后的两个三角形的位置改变,但形状、大小不变.
A
B
C
D
E
F
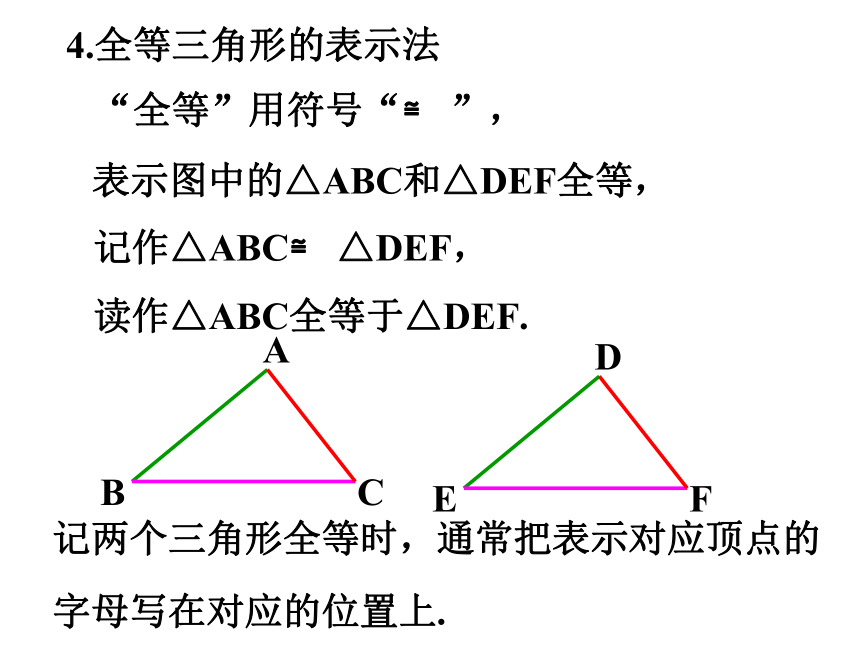
“全等”用符号“≌ ”,
表示图中的△ABC和△DEF全等,
4.全等三角形的表示法
记作△ABC≌ △DEF,
读作△ABC全等于△DEF.
记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
N
M
S
O
T
D
C
O
A
B
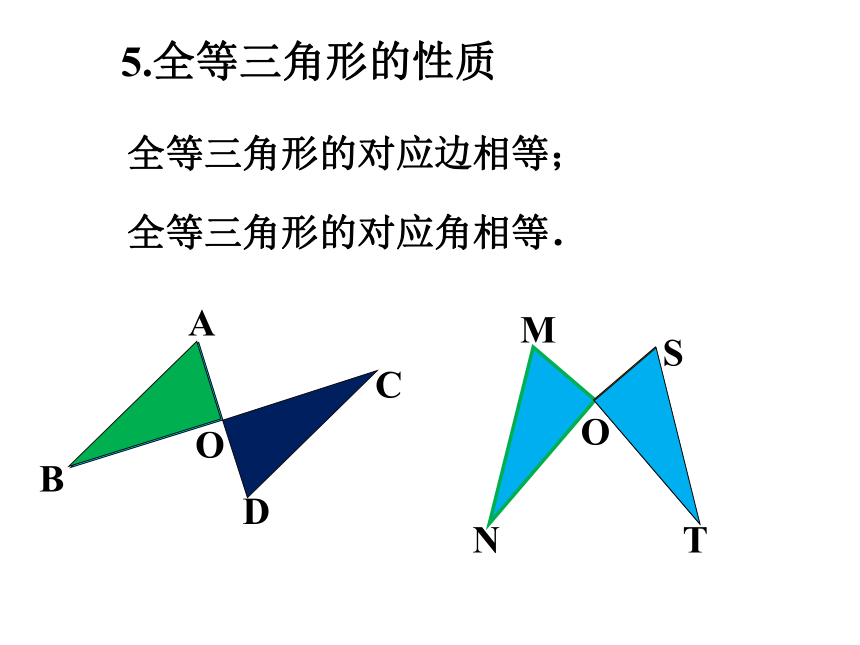
全等三角形的对应边相等;
5.全等三角形的性质
全等三角形的对应角相等.
A
B
C
D
E
F
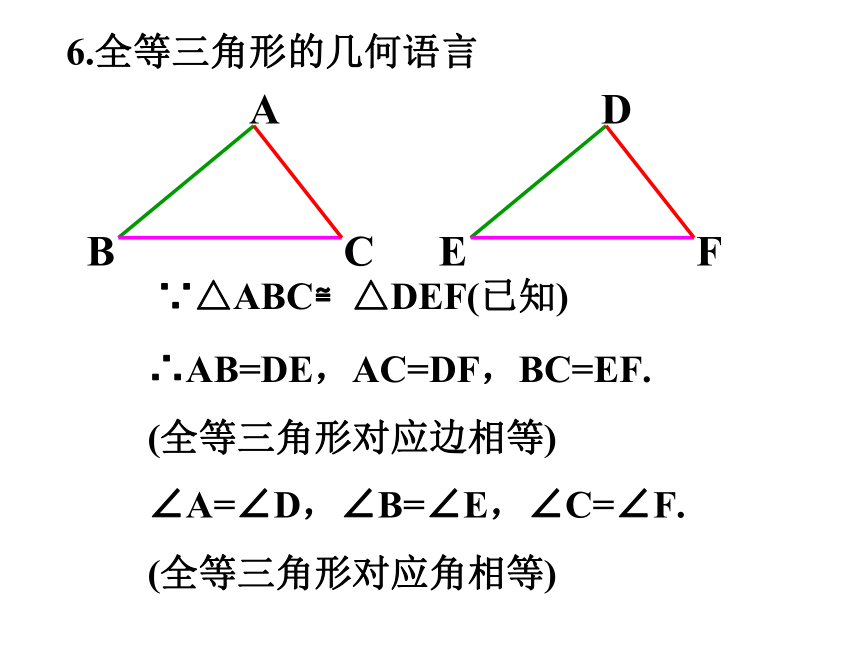
6.全等三角形的几何语言
∵△ABC≌△DEF(已知)
∴AB=DE,AC=DF,BC=EF.
(全等三角形对应边相等)
∠A=∠D,∠B=∠E,∠C=∠F.
(全等三角形对应角相等)
1.若△AOB≌△DOC,AO= ,
∠B= .
DO
∠C
公共点
D
C
O
A
B
练习巩固
2.若△ABC≌△DCB,AB= ,
∠ACB= .
DC
∠DBC
公共边
A
B
C
D
3.若△ABD≌△ACE,BD= ,
∠BDA= .
CE
∠CEA
A
B
C
D
E
公共角
在全等三角形中寻找对应边、对应角的规律一般是:
1.有公共边,则公共边为对应边
2.有公共角,则公共角为对应角 (对顶角为对应角)
3.最大边与最大边(最小边与最小边)为对应边;
最大角与最大角(最小角与最小角)为对应角.
4.对应角的对边为对应边;
5.对应边的对角为对应角.
6.根据书写规范,按照对应顶点找对应边或对应角.
(1)
(2)
(3)
(4)
A.(1)和(3)
B.(2)和(3)
C.(2)和(4)
D.(3)和(4)
1.下图中的四个图形是全等形的是( ).
巩固新知
C
2.观察下列图形,找出其中的全等形.
(1)和(9),
其中的全等形有:
(2)和(8),
(3)和(6).
3.观察下列三组全等图形,各是通过什么办法得到
(2)
(1)
(3)
(1)通过平移
(2)通过旋转
(3)通过翻折
4.添加适当的线,将九宫格分成全等的两个部分.
(1)如图,△ABC≌△DEF,AB和DE是对应边,
AC和DF是对应边,指出所有的对应角.
巩固提高
E
A
B
C
D
F
所有的对应角为:
∠B和∠E,
∠A和∠EDF,
∠BCA和∠EFD.
(2)如图,△ABE≌△DCF,∠AEB和∠DFC
是对应角,∠B和∠C是对应角,指出所有
的对应边.
A
B
C
D
E
F
所有的对应边为:
BE和CF,
AB和DC,
AE和DF.
(3)如图,△ABC≌△CDA,指出所有的对应边.
A
B
C
D
所有的对应边为:
BC和DA,
AB和CD,
AC和CA.
(4)如图,△ABC≌△EDC,指出所有的对应角.
A
B
C
D
E
所有的对应角为:
∠B和∠D,
∠A和∠E,
∠BCA和∠DCE.
(5)如图,△ABC≌△DEF,在△ABC中,BC
是最长边,∠ACB是最小角;在△DEF中,
EF是最长边,∠DFE是最小角.指出所有的
对应边和对应角.
A
B
C
D
E
F
所有的对应边为:
BC和EF,
AB和DE,
AC和DF.
所有的对应角为:
∠B和∠E,
∠A和∠D,
∠BCA和∠EFD.
今天作业
课本P95页第2、3 题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 八年级上册
14.1 全等三角形
教学目标
1.知道全等形,全等三角形的概念
2.知道全等三角形的性质
3.能识别全等三角形的对应边、对应角
教学重点:
识别全等三角形的对应边、对应角
教学难点:
识别全等三角形的对应边、对应角
看一看,下列同类的图形有什么特点.
能够完全重合的两个图形称为全等形.
1.全等形的定义
能够完全重合的两个三角形称为全等三角形.
2.全等三角形的定义
A
B
C
D
E
F
学习新知
A
B
C
D
E
F
3.把两个全等的三角形重叠到一起时,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角.
你能指出上面两个全等三角形的对应顶点、
对应边、对应角吗?
对应顶点
对应角
对应边
N
M
S
O
T
D
C
O
A
B
A
B
C
D
E
F
平移、翻折、旋转前后的两个三角形的位置改变,但形状、大小不变.
A
B
C
D
E
F
“全等”用符号“≌ ”,
表示图中的△ABC和△DEF全等,
4.全等三角形的表示法
记作△ABC≌ △DEF,
读作△ABC全等于△DEF.
记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
N
M
S
O
T
D
C
O
A
B
全等三角形的对应边相等;
5.全等三角形的性质
全等三角形的对应角相等.
A
B
C
D
E
F
6.全等三角形的几何语言
∵△ABC≌△DEF(已知)
∴AB=DE,AC=DF,BC=EF.
(全等三角形对应边相等)
∠A=∠D,∠B=∠E,∠C=∠F.
(全等三角形对应角相等)
1.若△AOB≌△DOC,AO= ,
∠B= .
DO
∠C
公共点
D
C
O
A
B
练习巩固
2.若△ABC≌△DCB,AB= ,
∠ACB= .
DC
∠DBC
公共边
A
B
C
D
3.若△ABD≌△ACE,BD= ,
∠BDA= .
CE
∠CEA
A
B
C
D
E
公共角
在全等三角形中寻找对应边、对应角的规律一般是:
1.有公共边,则公共边为对应边
2.有公共角,则公共角为对应角 (对顶角为对应角)
3.最大边与最大边(最小边与最小边)为对应边;
最大角与最大角(最小角与最小角)为对应角.
4.对应角的对边为对应边;
5.对应边的对角为对应角.
6.根据书写规范,按照对应顶点找对应边或对应角.
(1)
(2)
(3)
(4)
A.(1)和(3)
B.(2)和(3)
C.(2)和(4)
D.(3)和(4)
1.下图中的四个图形是全等形的是( ).
巩固新知
C
2.观察下列图形,找出其中的全等形.
(1)和(9),
其中的全等形有:
(2)和(8),
(3)和(6).
3.观察下列三组全等图形,各是通过什么办法得到
(2)
(1)
(3)
(1)通过平移
(2)通过旋转
(3)通过翻折
4.添加适当的线,将九宫格分成全等的两个部分.
(1)如图,△ABC≌△DEF,AB和DE是对应边,
AC和DF是对应边,指出所有的对应角.
巩固提高
E
A
B
C
D
F
所有的对应角为:
∠B和∠E,
∠A和∠EDF,
∠BCA和∠EFD.
(2)如图,△ABE≌△DCF,∠AEB和∠DFC
是对应角,∠B和∠C是对应角,指出所有
的对应边.
A
B
C
D
E
F
所有的对应边为:
BE和CF,
AB和DC,
AE和DF.
(3)如图,△ABC≌△CDA,指出所有的对应边.
A
B
C
D
所有的对应边为:
BC和DA,
AB和CD,
AC和CA.
(4)如图,△ABC≌△EDC,指出所有的对应角.
A
B
C
D
E
所有的对应角为:
∠B和∠D,
∠A和∠E,
∠BCA和∠DCE.
(5)如图,△ABC≌△DEF,在△ABC中,BC
是最长边,∠ACB是最小角;在△DEF中,
EF是最长边,∠DFE是最小角.指出所有的
对应边和对应角.
A
B
C
D
E
F
所有的对应边为:
BC和EF,
AB和DE,
AC和DF.
所有的对应角为:
∠B和∠E,
∠A和∠D,
∠BCA和∠EFD.
今天作业
课本P95页第2、3 题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
