第二十四章 圆 单元检测卷(含答案)
文档属性
| 名称 | 第二十四章 圆 单元检测卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 549.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-07 15:15:26 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
人教版九年级上《圆》单元检测试卷
选择题(本大题共10小题,每小题4分,满分40分)
1. 下列说法错误的是( )
A. 直径是弦 B. 最长的弦是直径
C. 垂直于弦的直径平分弦 D. 经过三点可以确定一个圆
2.如图AB是⊙O的直径,AC是⊙O的切线,A为切点,连结BC交圆O于点D,连结AD,若∠ABC=45°,则下列结论正确的是( )
A AD=BC B. AD=AC C. AC>AB D. AD>DC
3.如图,已知☉O的半径为7,弦AB的长为12,则圆心O到AB的距离为( )
B. 2 C. 2 D.
4.已知☉O的半径为5,且圆心O到直线l的距离是方程x2-4x-12=0的一个根,则直线l与圆的位置关系是( )
A. 相交 B. 相切 C. 相离 D. 无法确定
5.如图,在⊙O中,点A是的中点,∠ADC=24°,则∠AOB的度数是( )
A.24° B.26° C.48° D.66°
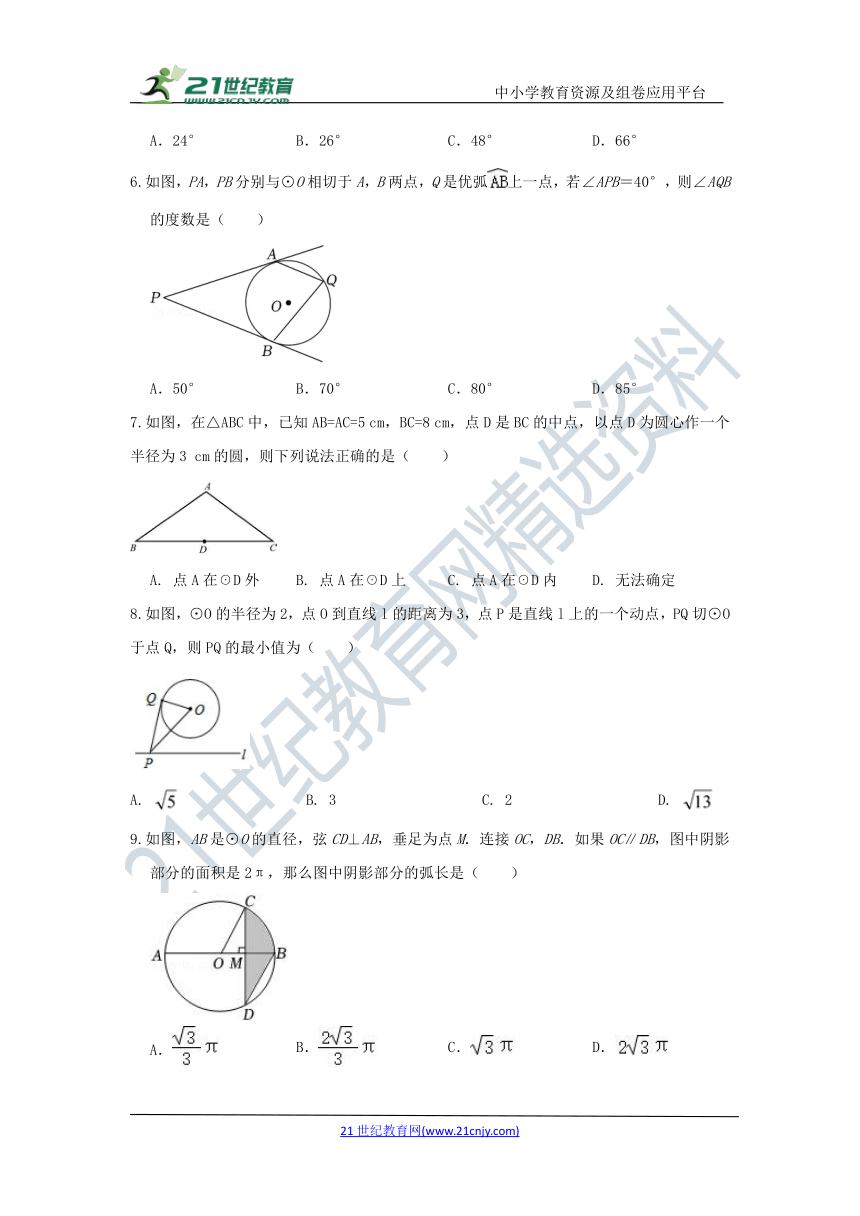
6.如图,PA,PB分别与⊙O相切于A,B两点,Q是优弧上一点,若∠APB=40°,则∠AQB的度数是( )
A.50° B.70° C.80° D.85°
7.如图,在△ABC中,已知AB=AC=5 cm,BC=8 cm,点D是BC的中点,以点D为圆心作一个半径为3 cm的圆,则下列说法正确的是( )
点A在☉D外 B. 点A在☉D上 C. 点A在☉D内 D. 无法确定
8.如图,⊙O的半径为2,点O到直线l的距离为3,点P是直线l上的一个动点,PQ切⊙O于点Q,则PQ的最小值为( )
B. 3 C. 2 D.
9.如图,AB是⊙O的直径,弦CD⊥AB,垂足为点M.连接OC,DB.如果OC∥DB,图中阴影部分的面积是2π,那么图中阴影部分的弧长是( )
B. C. D.
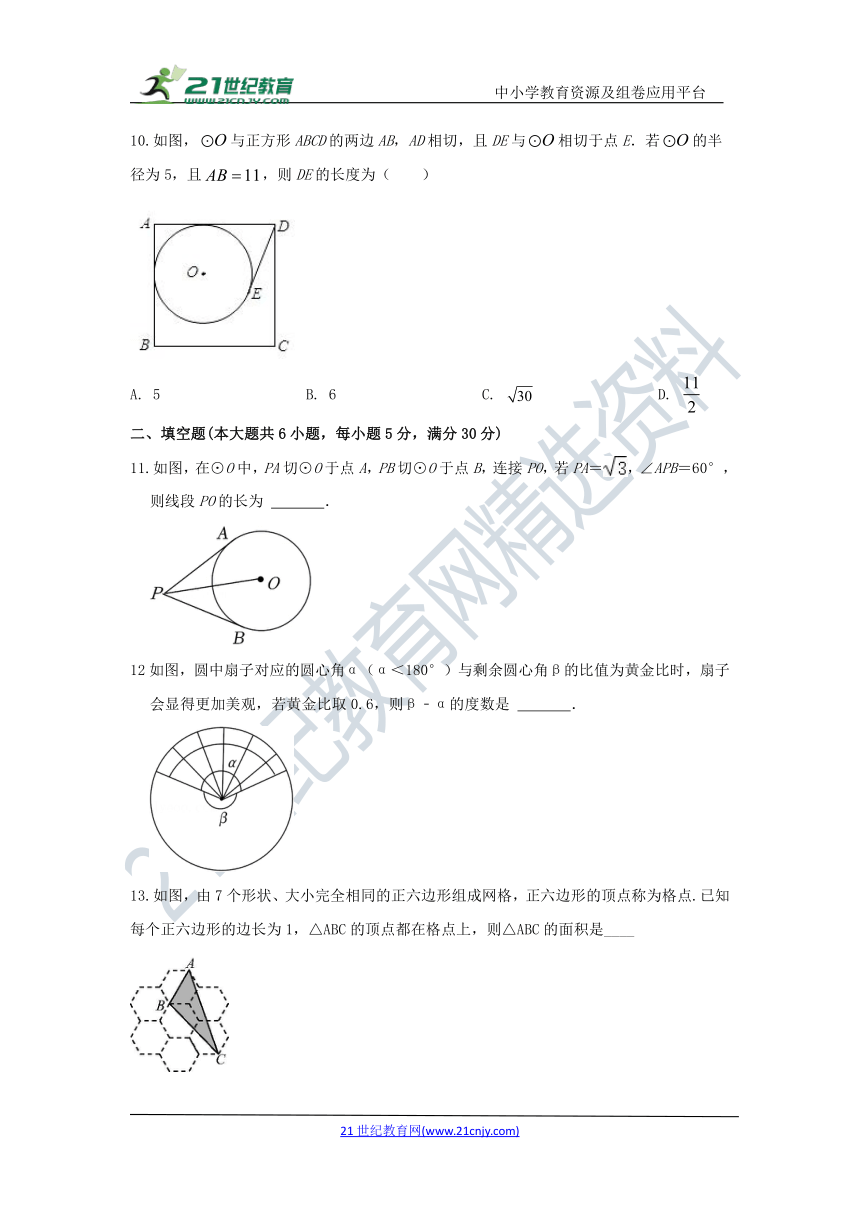
10.如图,与正方形ABCD的两边AB,AD相切,且DE与相切于点E.若的半径为5,且,则DE的长度为( )
5 B. 6 C. D.
二、填空题(本大题共6小题,每小题5分,满分30分)
11.如图,在⊙O中,PA切⊙O于点A,PB切⊙O于点B,连接PO,若PA=,∠APB=60°,则线段PO的长为 .
12如图,圆中扇子对应的圆心角α(α<180°)与剩余圆心角β的比值为黄金比时,扇子会显得更加美观,若黄金比取0.6,则β﹣α的度数是 .
13.如图,由7个形状、大小完全相同的正六边形组成网格,正六边形的顶点称为格点.已知每个正六边形的边长为1,△ABC的顶点都在格点上,则△ABC的面积是____
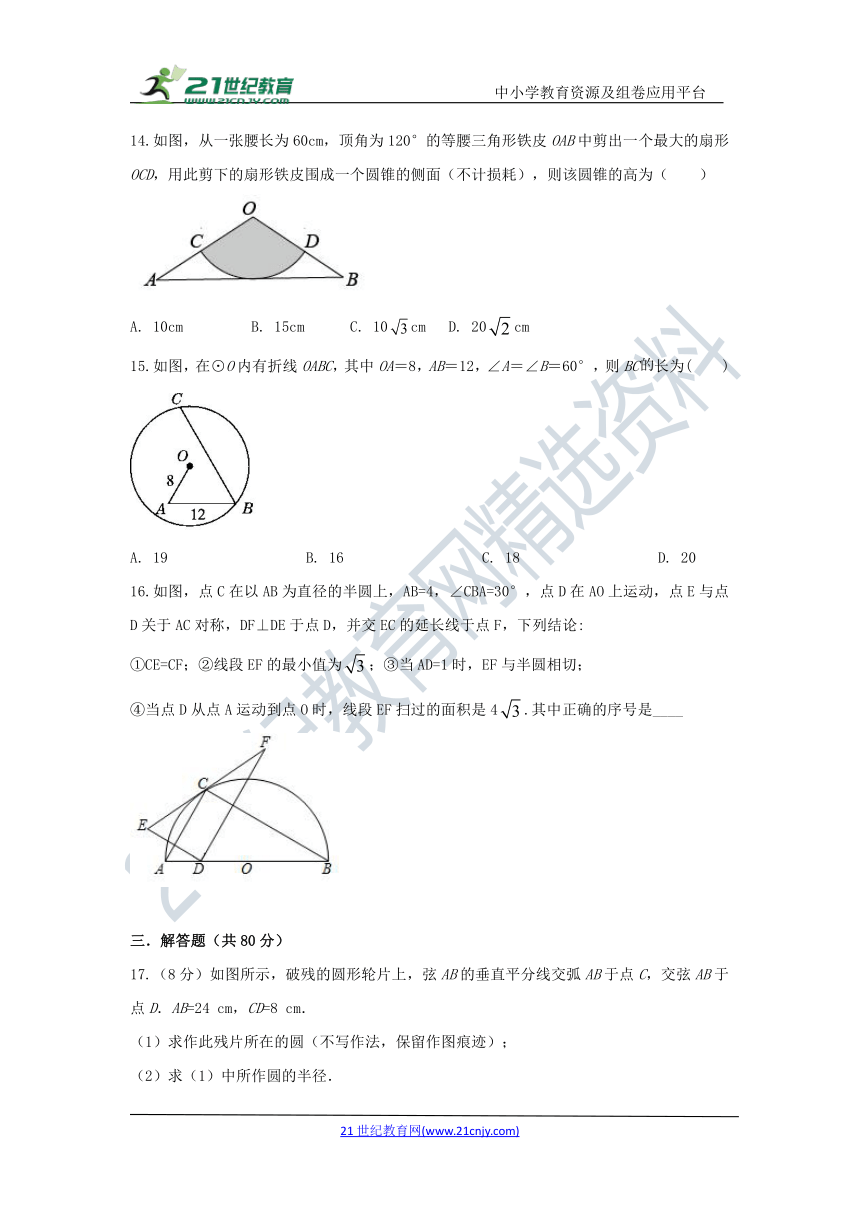
14.如图,从一张腰长为60cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的高为( )
10cm B. 15cm C. 10cm D. 20cm
15.如图,在⊙O内有折线OABC,其中OA=8,AB=12,∠A=∠B=60°,则BC长为( )
19 B. 16 C. 18 D. 20
16.如图,点C在以AB为直径的半圆上,AB=4,∠CBA=30°,点D在AO上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F,下列结论:
①CE=CF;②线段EF的最小值为;③当AD=1时,EF与半圆相切;
④当点D从点A运动到点O时,线段EF扫过的面积是4.其中正确的序号是____
三.解答题(共80分)
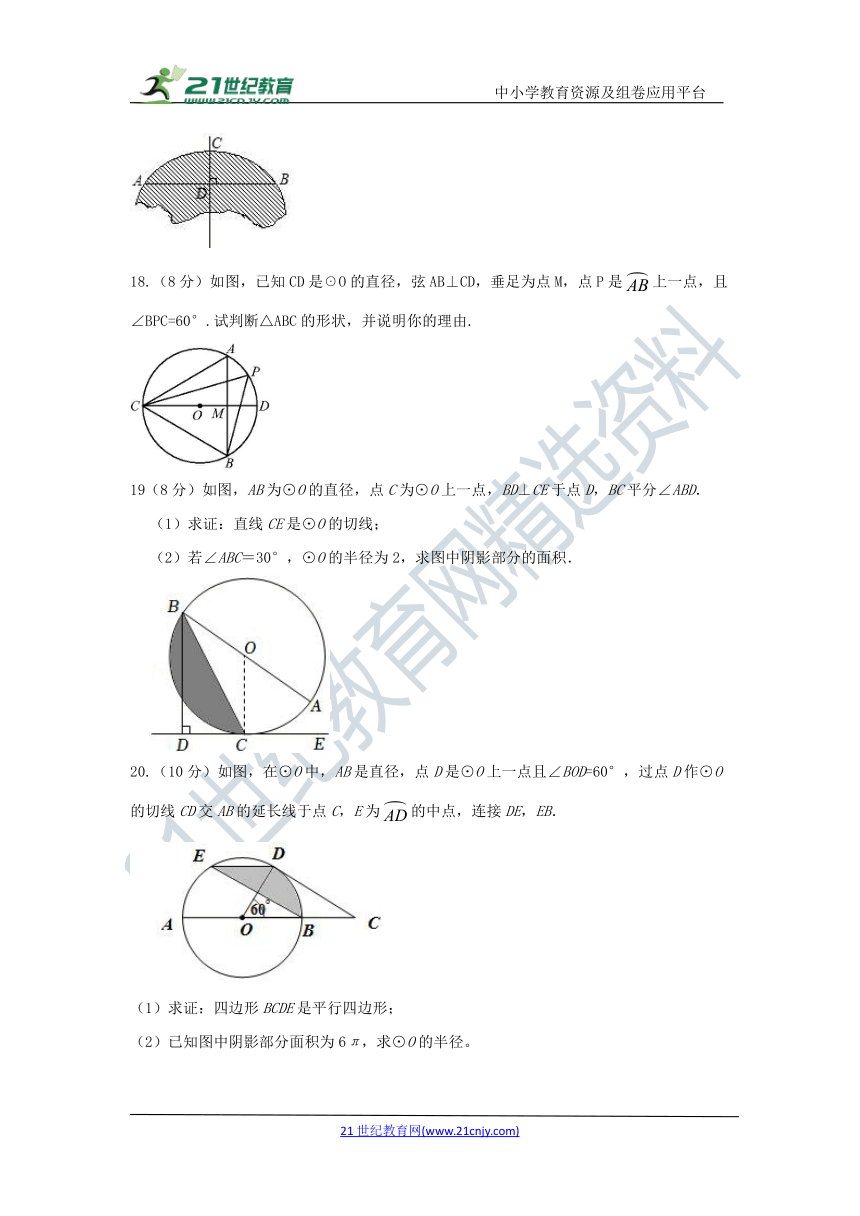
17.(8分)如图所示,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.AB=24 cm,CD=8 cm.
(1)求作此残片所在的圆(不写作法,保留作图痕迹);
(2)求(1)中所作圆的半径.
18.(8分)如图,已知CD是☉O的直径,弦AB⊥CD,垂足为点M,点P是上一点,且∠BPC=60°.试判断△ABC的形状,并说明你的理由.
19(8分)如图,AB为⊙O的直径,点C为⊙O上一点,BD⊥CE于点D,BC平分∠ABD.
(1)求证:直线CE是⊙O的切线;
(2)若∠ABC=30°,⊙O的半径为2,求图中阴影部分的面积.
20.(10分)如图,在⊙O中,AB是直径,点D是⊙O上一点且∠BOD=60°,过点D作⊙O的切线CD交AB的延长线于点C,E为的中点,连接DE,EB.
(1)求证:四边形BCDE是平行四边形;
(2)已知图中阴影部分面积为6π,求⊙O的半径。
21.(10分) 如图,已知为⊙O的直径且,点(不与重合)为⊙O上一个动点,线段经过点,且为⊙O上一点,的延长线与的延长线交于点.
(1)求证:;
(2)当点在⊙O上移动时,求四边形的最大面积。
22.(10分)如图,AB是⊙O的直径,点D是AB延长线上的一点,DC与⊙O相切于点C.连接BC,AC.
(1)求证:∠A=∠BCD;
(2)若∠D=45°,⊙O的半径为2,求线段AD的长.
23.(12分)已知AB是半圆O的直径,点C是半圆O上的动点,点D是线段AB延长线上的动点,在运动过程中,保持CD=OA.
(1)当直线CD与半圆O相切时(如图①),求∠ODC的度数;
(2)当直线CD与半圆O相交时(如图②),设另一交点为E,连接AE,若AE∥OC.
①AE与OD的大小有什么关系 为什么
②求∠ODC的度数.
24.(14分)如图,点P在射线AB的上方,且∠PAB=45°,PA=2,点M是射线AB上的动点(点M不与点A重合),现将点P绕点A按顺时针方向旋转60°到点Q,将点M绕点P按逆时针方向旋转60°到点N,连接AQ,PM,PN,作直线QN.
(1)求证:AM=QN
(2)直线QN与以点P为圆心,以PN长为半径的圆是否存在相切的情况 若存在,请求出此时AM的长,若不存在,请说明理由.
(3)当以点P为圆心,以PN的长为半径的圆经过点Q时,直接写出劣弧NQ与两条半径所围成的扇形的面积.
答案:
D
A
D
C
C
B
B
A
B
B
2
2
20
20
①③
17.解:(1)作弦AC的垂直平分线与弦AB的垂直平分线交于O点,以O为圆心OA长为半径作圆O就是此残片所在的圆,如图.
(2)连接OA,设OA=x,AD=12cm,OD=(x-8)cm,
则根据勾股定理列方程:
x2=122+(x-8)2,解得:x=13
答:圆的半径为13cm.
18.解:△ABC为等边三角形.理由如下:
∵AB⊥CD,CD为⊙O的直径,
∴弧AC=弧BC,
∴AC=BC,
又∵∠BPC=∠A=60°,
∴△ABC为等边三角形.
19:(1)连接OC.
∵OA=OC,
∴∠CAO=∠OCA,
∵∠DAC=∠CAO,
∴∠DAC=∠OCA,
∴AD∥OC;
又∵CD⊥AD,
∴OC⊥CD,
∴CD是⊙O的切线
过O点作OM⊥BC于M,
∵∠ABC=30°,⊙O的半径为2
∴OM=1,BC=2,∠BOC=
阴影部分的面积= — ×1×2=π —
20.解:(1)∵CD是⊙O的切线,∴∠CDO=90°,∵∠BOD=60°,
∴∠C=30°,∠AOD=120°,
∵E为 E为的中点,
∴∠AOE=∠DOE=60°,
∴∠BOE=120°,
∵OE=OB,
∴∠OEB=∠OBE=30°,
∴∠C=∠OBE=∠E,
∴DE∥BC,BE∥CD,
∴四边形BCDE是平行四边形;
(2)连接OE,由(1)知,
∠BOE=120°,
∵阴影部分面积为6π,
∴=6π, ∴r=6
21.解:(1)连接FA,
∵∠FEB=90°,
∴EF⊥AB,
∵BE=AE,
∴BF=AF,
∵∠FEA=∠FEB=90°,
∴AF是⊙O的直径,
∴AF=DE,
∴BF=ED,
在Rt△EFB与Rt△ADE中,BE=AE,BF=DE
∴Rt△EFB≌Rt△ADE;
(2)∵Rt△EFB≌Rt△ADE,
∴∠B=∠AED,
∴DE∥BC,
∵ED为⊙O的直径,
∴AC⊥AB,
∵EF⊥AB,
∴EF∥CD,
∴四边形FCDE是平行四边形,
∴E到BC的距离最大时,四边形FCDE的面积最大,
即点A到DE的距离最大,
∴当A为弧DE的中点时,
点A到DE的距离最大是2,
∴四边形FCDE的最大面积=4×2=8
22. (1)证明:连接OC,
∵AB是⊙O的直径,∴∠ACO+∠BCO=900
∵DC与⊙O相切于点C,∴∠BCO+∠BCD=900
∵OC=OA,∴∠A=∠ACO
∴∠A=∠BCD
(2)∵∠CDB=450,,
由(1)得,容易得出AD=2+2
23.(1)如图①,连接OC,
∵OC=OA,CD=OA,
∴OC=CD,
∴∠ODC=∠COD,
∵CD是⊙O的切线,
∴∠OCD=90°,
∴∠ODC=45°;
(2)如图②,连接OE.
∵CD=OA,∴CD=OC=OE=OA,
∴∠1=∠2,∠3=∠4.
∵AE∥OC,
∴∠2=∠3.
设∠ODC=∠1=x,则∠2=∠3=∠4=x.
∴∠AOE=∠OCD=180°-2x.
①AE=OD.理由如下:
在△AOE与△OCD中,
∴△AOE≌△OCD(SAS),
∴AE=OD.
②∠6=∠1+∠2=2x.
∵OE=OC,∴∠5=∠6=2x.
∵AE∥OC,
∴∠4+∠5+∠6=180°,即:x+2x+2x=180°,
∴x=36°.
∴∠ODC=36°
24.(1)证明:如图1,
连接PQ,
由点P绕点A按顺时针方向旋转60°到点Q,
可得,AP=AQ,∠PAQ=60°,
∴△APQ为等边三角形,
∴PA=PQ,∠APQ=60°,
由点M绕点P按逆时针方向旋转60°到点N,
可得,PM=PN,∠MPN=60°,
∴∠APM=∠QPN,
则△APM≌△QPN(SAS),
∴AM=QN
存在.
如图2,由(1)中的证明可知,△APM≌△QPN,
∴∠AMP=∠QNP,
∵直线QN与以点P为圆心,以PN的长为半径的圆相切,
∴∠AMP=∠QNP=90°,
即:PN⊥QN,
在R△APM中,∠PAB=45°,PA=2,
∴AM=
如图3,由(1)知,△APQ是等边三角形,
∴PA=PQ,∠APQ=60°,
∵以点P为圆心,以PN的长为半径的圆经过点Q,
∴PN=PQ=PA,
∵PM=PN,
∴PA=PM,
∵∠PAB=45°,
∴∠APM=90°,
∴∠MPQ=∠APM-∠APQ=30°,
∵∠MPN=60°,
∴∠QPN=90°
∴劣弧NQ与两条半径所围成的扇形的面积是扇形QPN的面积,而此扇形的圆心角∠QPN=90°,半径为PN=PM=PA=2,
∴劣弧NQ与两条半径所围成的扇形的面积=
90π 22
360
=π.
21世纪教育网(www.21cnjy.com)
人教版九年级上《圆》单元检测试卷
选择题(本大题共10小题,每小题4分,满分40分)
1. 下列说法错误的是( )
A. 直径是弦 B. 最长的弦是直径
C. 垂直于弦的直径平分弦 D. 经过三点可以确定一个圆
2.如图AB是⊙O的直径,AC是⊙O的切线,A为切点,连结BC交圆O于点D,连结AD,若∠ABC=45°,则下列结论正确的是( )
A AD=BC B. AD=AC C. AC>AB D. AD>DC
3.如图,已知☉O的半径为7,弦AB的长为12,则圆心O到AB的距离为( )
B. 2 C. 2 D.
4.已知☉O的半径为5,且圆心O到直线l的距离是方程x2-4x-12=0的一个根,则直线l与圆的位置关系是( )
A. 相交 B. 相切 C. 相离 D. 无法确定
5.如图,在⊙O中,点A是的中点,∠ADC=24°,则∠AOB的度数是( )
A.24° B.26° C.48° D.66°
6.如图,PA,PB分别与⊙O相切于A,B两点,Q是优弧上一点,若∠APB=40°,则∠AQB的度数是( )
A.50° B.70° C.80° D.85°
7.如图,在△ABC中,已知AB=AC=5 cm,BC=8 cm,点D是BC的中点,以点D为圆心作一个半径为3 cm的圆,则下列说法正确的是( )
点A在☉D外 B. 点A在☉D上 C. 点A在☉D内 D. 无法确定
8.如图,⊙O的半径为2,点O到直线l的距离为3,点P是直线l上的一个动点,PQ切⊙O于点Q,则PQ的最小值为( )
B. 3 C. 2 D.
9.如图,AB是⊙O的直径,弦CD⊥AB,垂足为点M.连接OC,DB.如果OC∥DB,图中阴影部分的面积是2π,那么图中阴影部分的弧长是( )
B. C. D.
10.如图,与正方形ABCD的两边AB,AD相切,且DE与相切于点E.若的半径为5,且,则DE的长度为( )
5 B. 6 C. D.
二、填空题(本大题共6小题,每小题5分,满分30分)
11.如图,在⊙O中,PA切⊙O于点A,PB切⊙O于点B,连接PO,若PA=,∠APB=60°,则线段PO的长为 .
12如图,圆中扇子对应的圆心角α(α<180°)与剩余圆心角β的比值为黄金比时,扇子会显得更加美观,若黄金比取0.6,则β﹣α的度数是 .
13.如图,由7个形状、大小完全相同的正六边形组成网格,正六边形的顶点称为格点.已知每个正六边形的边长为1,△ABC的顶点都在格点上,则△ABC的面积是____
14.如图,从一张腰长为60cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的高为( )
10cm B. 15cm C. 10cm D. 20cm
15.如图,在⊙O内有折线OABC,其中OA=8,AB=12,∠A=∠B=60°,则BC长为( )
19 B. 16 C. 18 D. 20
16.如图,点C在以AB为直径的半圆上,AB=4,∠CBA=30°,点D在AO上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F,下列结论:
①CE=CF;②线段EF的最小值为;③当AD=1时,EF与半圆相切;
④当点D从点A运动到点O时,线段EF扫过的面积是4.其中正确的序号是____
三.解答题(共80分)
17.(8分)如图所示,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.AB=24 cm,CD=8 cm.
(1)求作此残片所在的圆(不写作法,保留作图痕迹);
(2)求(1)中所作圆的半径.
18.(8分)如图,已知CD是☉O的直径,弦AB⊥CD,垂足为点M,点P是上一点,且∠BPC=60°.试判断△ABC的形状,并说明你的理由.
19(8分)如图,AB为⊙O的直径,点C为⊙O上一点,BD⊥CE于点D,BC平分∠ABD.
(1)求证:直线CE是⊙O的切线;
(2)若∠ABC=30°,⊙O的半径为2,求图中阴影部分的面积.
20.(10分)如图,在⊙O中,AB是直径,点D是⊙O上一点且∠BOD=60°,过点D作⊙O的切线CD交AB的延长线于点C,E为的中点,连接DE,EB.
(1)求证:四边形BCDE是平行四边形;
(2)已知图中阴影部分面积为6π,求⊙O的半径。
21.(10分) 如图,已知为⊙O的直径且,点(不与重合)为⊙O上一个动点,线段经过点,且为⊙O上一点,的延长线与的延长线交于点.
(1)求证:;
(2)当点在⊙O上移动时,求四边形的最大面积。
22.(10分)如图,AB是⊙O的直径,点D是AB延长线上的一点,DC与⊙O相切于点C.连接BC,AC.
(1)求证:∠A=∠BCD;
(2)若∠D=45°,⊙O的半径为2,求线段AD的长.
23.(12分)已知AB是半圆O的直径,点C是半圆O上的动点,点D是线段AB延长线上的动点,在运动过程中,保持CD=OA.
(1)当直线CD与半圆O相切时(如图①),求∠ODC的度数;
(2)当直线CD与半圆O相交时(如图②),设另一交点为E,连接AE,若AE∥OC.
①AE与OD的大小有什么关系 为什么
②求∠ODC的度数.
24.(14分)如图,点P在射线AB的上方,且∠PAB=45°,PA=2,点M是射线AB上的动点(点M不与点A重合),现将点P绕点A按顺时针方向旋转60°到点Q,将点M绕点P按逆时针方向旋转60°到点N,连接AQ,PM,PN,作直线QN.
(1)求证:AM=QN
(2)直线QN与以点P为圆心,以PN长为半径的圆是否存在相切的情况 若存在,请求出此时AM的长,若不存在,请说明理由.
(3)当以点P为圆心,以PN的长为半径的圆经过点Q时,直接写出劣弧NQ与两条半径所围成的扇形的面积.
答案:
D
A
D
C
C
B
B
A
B
B
2
2
20
20
①③
17.解:(1)作弦AC的垂直平分线与弦AB的垂直平分线交于O点,以O为圆心OA长为半径作圆O就是此残片所在的圆,如图.
(2)连接OA,设OA=x,AD=12cm,OD=(x-8)cm,
则根据勾股定理列方程:
x2=122+(x-8)2,解得:x=13
答:圆的半径为13cm.
18.解:△ABC为等边三角形.理由如下:
∵AB⊥CD,CD为⊙O的直径,
∴弧AC=弧BC,
∴AC=BC,
又∵∠BPC=∠A=60°,
∴△ABC为等边三角形.
19:(1)连接OC.
∵OA=OC,
∴∠CAO=∠OCA,
∵∠DAC=∠CAO,
∴∠DAC=∠OCA,
∴AD∥OC;
又∵CD⊥AD,
∴OC⊥CD,
∴CD是⊙O的切线
过O点作OM⊥BC于M,
∵∠ABC=30°,⊙O的半径为2
∴OM=1,BC=2,∠BOC=
阴影部分的面积= — ×1×2=π —
20.解:(1)∵CD是⊙O的切线,∴∠CDO=90°,∵∠BOD=60°,
∴∠C=30°,∠AOD=120°,
∵E为 E为的中点,
∴∠AOE=∠DOE=60°,
∴∠BOE=120°,
∵OE=OB,
∴∠OEB=∠OBE=30°,
∴∠C=∠OBE=∠E,
∴DE∥BC,BE∥CD,
∴四边形BCDE是平行四边形;
(2)连接OE,由(1)知,
∠BOE=120°,
∵阴影部分面积为6π,
∴=6π, ∴r=6
21.解:(1)连接FA,
∵∠FEB=90°,
∴EF⊥AB,
∵BE=AE,
∴BF=AF,
∵∠FEA=∠FEB=90°,
∴AF是⊙O的直径,
∴AF=DE,
∴BF=ED,
在Rt△EFB与Rt△ADE中,BE=AE,BF=DE
∴Rt△EFB≌Rt△ADE;
(2)∵Rt△EFB≌Rt△ADE,
∴∠B=∠AED,
∴DE∥BC,
∵ED为⊙O的直径,
∴AC⊥AB,
∵EF⊥AB,
∴EF∥CD,
∴四边形FCDE是平行四边形,
∴E到BC的距离最大时,四边形FCDE的面积最大,
即点A到DE的距离最大,
∴当A为弧DE的中点时,
点A到DE的距离最大是2,
∴四边形FCDE的最大面积=4×2=8
22. (1)证明:连接OC,
∵AB是⊙O的直径,∴∠ACO+∠BCO=900
∵DC与⊙O相切于点C,∴∠BCO+∠BCD=900
∵OC=OA,∴∠A=∠ACO
∴∠A=∠BCD
(2)∵∠CDB=450,,
由(1)得,容易得出AD=2+2
23.(1)如图①,连接OC,
∵OC=OA,CD=OA,
∴OC=CD,
∴∠ODC=∠COD,
∵CD是⊙O的切线,
∴∠OCD=90°,
∴∠ODC=45°;
(2)如图②,连接OE.
∵CD=OA,∴CD=OC=OE=OA,
∴∠1=∠2,∠3=∠4.
∵AE∥OC,
∴∠2=∠3.
设∠ODC=∠1=x,则∠2=∠3=∠4=x.
∴∠AOE=∠OCD=180°-2x.
①AE=OD.理由如下:
在△AOE与△OCD中,
∴△AOE≌△OCD(SAS),
∴AE=OD.
②∠6=∠1+∠2=2x.
∵OE=OC,∴∠5=∠6=2x.
∵AE∥OC,
∴∠4+∠5+∠6=180°,即:x+2x+2x=180°,
∴x=36°.
∴∠ODC=36°
24.(1)证明:如图1,
连接PQ,
由点P绕点A按顺时针方向旋转60°到点Q,
可得,AP=AQ,∠PAQ=60°,
∴△APQ为等边三角形,
∴PA=PQ,∠APQ=60°,
由点M绕点P按逆时针方向旋转60°到点N,
可得,PM=PN,∠MPN=60°,
∴∠APM=∠QPN,
则△APM≌△QPN(SAS),
∴AM=QN
存在.
如图2,由(1)中的证明可知,△APM≌△QPN,
∴∠AMP=∠QNP,
∵直线QN与以点P为圆心,以PN的长为半径的圆相切,
∴∠AMP=∠QNP=90°,
即:PN⊥QN,
在R△APM中,∠PAB=45°,PA=2,
∴AM=
如图3,由(1)知,△APQ是等边三角形,
∴PA=PQ,∠APQ=60°,
∵以点P为圆心,以PN的长为半径的圆经过点Q,
∴PN=PQ=PA,
∵PM=PN,
∴PA=PM,
∵∠PAB=45°,
∴∠APM=90°,
∴∠MPQ=∠APM-∠APQ=30°,
∵∠MPN=60°,
∴∠QPN=90°
∴劣弧NQ与两条半径所围成的扇形的面积是扇形QPN的面积,而此扇形的圆心角∠QPN=90°,半径为PN=PM=PA=2,
∴劣弧NQ与两条半径所围成的扇形的面积=
90π 22
360
=π.
21世纪教育网(www.21cnjy.com)
同课章节目录
