人教版数学八年级上册 15 分式第1课时 课件(共34张PPT)
文档属性
| 名称 | 人教版数学八年级上册 15 分式第1课时 课件(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 576.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-07 15:15:40 | ||
图片预览




文档简介
(共34张PPT)
第1课时
分式
八年级上册 RJ
初中数学
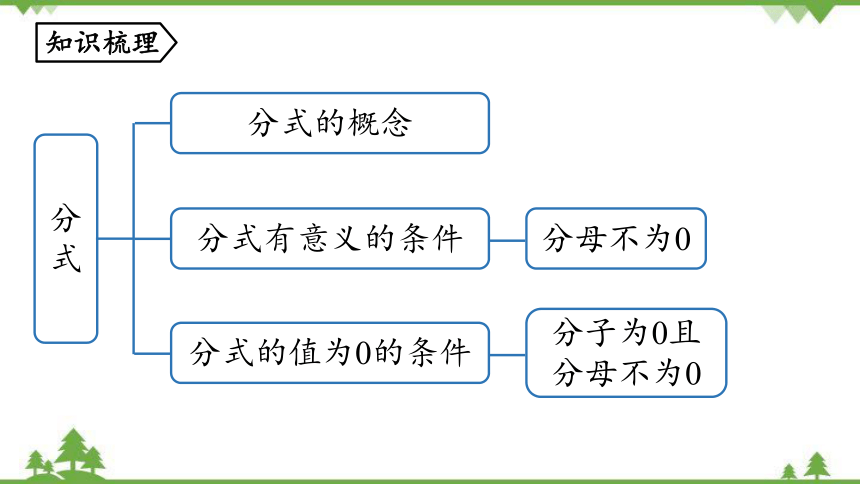
分式
分式的概念
分式有意义的条件
分式的值为0的条件
分母不为0
分子为0且分母不为0
知识梳理
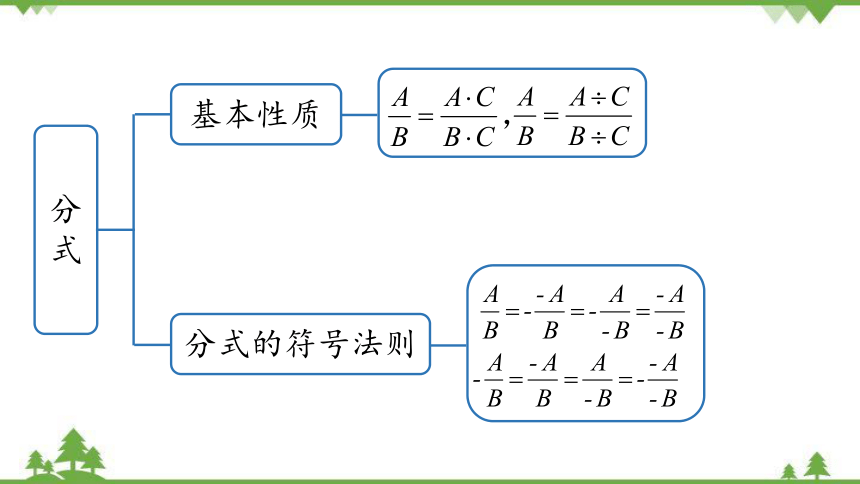
分式
基本性质
分式的符号法则
,
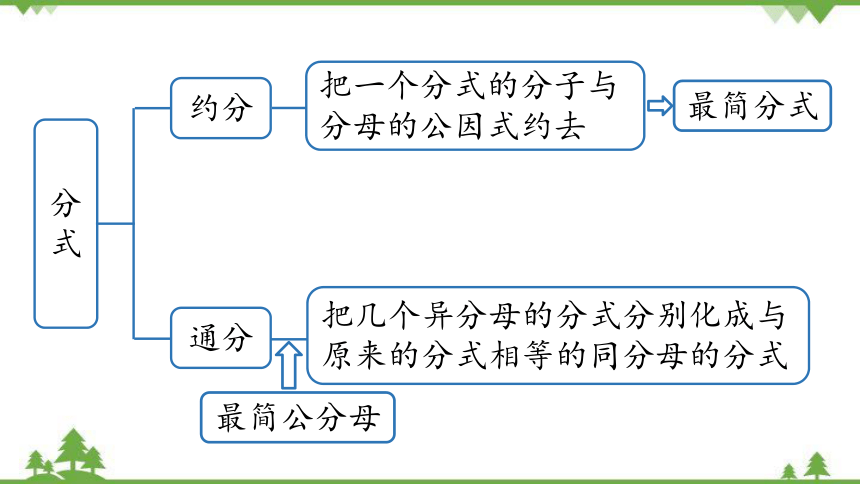
分式
约分
通分
把一个分式的分子与分母的公因式约去
把几个异分母的分式分别化成与原来的分式相等的同分母的分式
最简分式
最简公分母
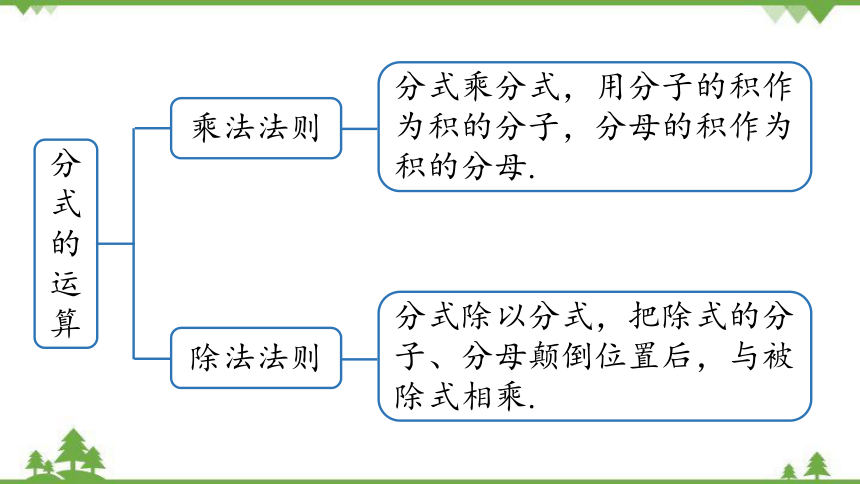
分式的运算
乘法法则
除法法则
分式乘分式,用分子的积作为积的分子,分母的积作为积的分母.
分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘.
分式的运算
分式的乘方法则
分式的乘除、乘方
混合运算法则
分式乘方要把分子、分母分别乘方.
先乘方,再乘除,有括号的先算括号里面的.
分式的运算
同分母分式相加减
异分母分式相加减
分母不变,把分子相加减
先通分,变为同分母的分式,再加减
分式的运算
分式的混合运算
熟练运用分式的混合运算法则进行计算
先算乘方,再算乘除,最后算加减;若有括号,则先算括号里面的;同级运算,按从左到右的顺序进行计算.
整数指数幂的运算性质
同底数幂的乘法
幂的乘方
am·an=am+n(m,n是整数)
(am)n=amn(m,n是整数)
积的乘方
(ab)n=anbn(n是整数)
同底数幂的除法
am÷an=am-n(m,n是整数,a≠0)
分数的乘方
(n是整数,b≠0)
科学记数法
表示较小的数
确定n的方法
小于1的正数可以用科学记数法表示为a×10-n的形式,其中1≤a<10,n是正整数.
n等于原数中左起第一个非0数前0的个数(包括小数点前的那个0)
小数点向右移到第一个非0的数后,小数点移动了几位,n就等于几
分式的概念
一般地,如果A、B表示两个整式,并且B中含有字母,那么式子 叫做分式. 分式 中,A叫做分子,B叫做分母.
分式无意义的条件:
分式的分母表示除数,由于除数不能为0,所以分式的分母不能为0,即当B≠0时,分式 才有意义.
分式的分母为0,即当B=0时,分式 无意义.
分式有意义的条件:
分式的值为0的条件:
当分式的分子等于0且分母不等于0时,分式的值为0.
分式的基本性质
分式的分子与分母乘(或除以)同一个不为0的整式,分式的值不变.
式子表示
, (C≠0),
其中A,B,C是整式.
分式的分子、分母与分式本身这三处的正负号,同时改变两处,分式的值不变.
分式的符号法则
用式子表示:
或
分式的约分:
根据分式的基本性质,把一个分式的分子与分母的公因式约去,叫做分式的约分.
最简分式:
分子与分母没有公因式的分式,叫做最简分式.
分式的通分:
根据分式的基本性质,把几个异分母的分式分别化成与原来的分式相等的同分母的分式,叫做分式的通分.
最简公分母:
通分时,一般取各分母的所有因式的最高次幂的积作为公分母,这样的分母叫做最简公分母.
分式的乘法法则
分式乘分式,用分子的积作为积的分子,分母的积作为积的分母.
用式子表示: .
分式的除法法则
分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘.
用式子表示: .
分式的乘方法则
分式乘方要把分子、分母分别乘方.
用式子表示: (n为正整数).
分式的加减法法则
同分母分式相加减,分母不变,把分子相加减.
用式子表示: .
异分母分式相加减,先通分,变为同分母的分式,再加减.
分式的混合运算顺序:
先算乘方,再算乘除,最后算加减;若有括号,则先算括号里面的;同级运算,按从左到右的顺序进行计算.
负整数指数幂
一般地,当n是正整数时, (a≠0).
这就是说 (a≠0)是 的倒数.
负整数指数幂的三个常用结论:
(1)an与a-n互为倒数;
(3) .
(2) ;
用科学记数法表示小于1的正数
小于1的正数可以用科学记数法表示为a×10-n的形式,其中1≤a<10,n是正整数.
科学记数法是一种记数方法,不改变此数的性质和大小,用科学记数法表示一个负数时,不要忘了前面带“-”号,用科学记数法表示一个带有单位的数时,其表示结果也应带有单位.
1.(1)分式 有意义的条件是__________,值为零的条件是_____.
(2)分式 无意义的条件是______,值为零的条件是____.
x≠1且x≠2
x=±3
x=-2
x=0
重难剖析
2.下列等式从左到右变形一定正确的是( )
C
A. B.
C. D.
没有说明c是否为0
c在等号左边,且在分母上,说明c不为0
3.计算:
解:(1)原式
(1) ;
解:(2)原式
3.计算:
(2) ;
解:(1)原式
4.计算:
(1) ; (2) .
4.计算:
(1) ; (2) .
解:(2)原式
5.用科学记数法表示下列各数:
(1) 0.00001; (2) 0.000000567;
(3) 0.000000301; (4) -0.0023.
解:(1) 0.00001=1×10-5 ;
(2) 0.000000567=5.67×10-7 ;
(3) 0.000000301=3.01×10-7 ;
(4) -0.0023=-2.3×10-3 .
解:(1)原式
能力提升
1.计算:
(1) ; (2) .
解:(2)原式
1.计算:
(1) ; (2) .
解:原式
则不等式组的整数解有-1、0、1、2,
当x=1、-1、0时,原式无意义.
所以x=2,原式=0.
解不等式组得 .
代入原式的值必须使原式有意义.
第1课时
分式
八年级上册 RJ
初中数学
分式
分式的概念
分式有意义的条件
分式的值为0的条件
分母不为0
分子为0且分母不为0
知识梳理
分式
基本性质
分式的符号法则
,
分式
约分
通分
把一个分式的分子与分母的公因式约去
把几个异分母的分式分别化成与原来的分式相等的同分母的分式
最简分式
最简公分母
分式的运算
乘法法则
除法法则
分式乘分式,用分子的积作为积的分子,分母的积作为积的分母.
分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘.
分式的运算
分式的乘方法则
分式的乘除、乘方
混合运算法则
分式乘方要把分子、分母分别乘方.
先乘方,再乘除,有括号的先算括号里面的.
分式的运算
同分母分式相加减
异分母分式相加减
分母不变,把分子相加减
先通分,变为同分母的分式,再加减
分式的运算
分式的混合运算
熟练运用分式的混合运算法则进行计算
先算乘方,再算乘除,最后算加减;若有括号,则先算括号里面的;同级运算,按从左到右的顺序进行计算.
整数指数幂的运算性质
同底数幂的乘法
幂的乘方
am·an=am+n(m,n是整数)
(am)n=amn(m,n是整数)
积的乘方
(ab)n=anbn(n是整数)
同底数幂的除法
am÷an=am-n(m,n是整数,a≠0)
分数的乘方
(n是整数,b≠0)
科学记数法
表示较小的数
确定n的方法
小于1的正数可以用科学记数法表示为a×10-n的形式,其中1≤a<10,n是正整数.
n等于原数中左起第一个非0数前0的个数(包括小数点前的那个0)
小数点向右移到第一个非0的数后,小数点移动了几位,n就等于几
分式的概念
一般地,如果A、B表示两个整式,并且B中含有字母,那么式子 叫做分式. 分式 中,A叫做分子,B叫做分母.
分式无意义的条件:
分式的分母表示除数,由于除数不能为0,所以分式的分母不能为0,即当B≠0时,分式 才有意义.
分式的分母为0,即当B=0时,分式 无意义.
分式有意义的条件:
分式的值为0的条件:
当分式的分子等于0且分母不等于0时,分式的值为0.
分式的基本性质
分式的分子与分母乘(或除以)同一个不为0的整式,分式的值不变.
式子表示
, (C≠0),
其中A,B,C是整式.
分式的分子、分母与分式本身这三处的正负号,同时改变两处,分式的值不变.
分式的符号法则
用式子表示:
或
分式的约分:
根据分式的基本性质,把一个分式的分子与分母的公因式约去,叫做分式的约分.
最简分式:
分子与分母没有公因式的分式,叫做最简分式.
分式的通分:
根据分式的基本性质,把几个异分母的分式分别化成与原来的分式相等的同分母的分式,叫做分式的通分.
最简公分母:
通分时,一般取各分母的所有因式的最高次幂的积作为公分母,这样的分母叫做最简公分母.
分式的乘法法则
分式乘分式,用分子的积作为积的分子,分母的积作为积的分母.
用式子表示: .
分式的除法法则
分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘.
用式子表示: .
分式的乘方法则
分式乘方要把分子、分母分别乘方.
用式子表示: (n为正整数).
分式的加减法法则
同分母分式相加减,分母不变,把分子相加减.
用式子表示: .
异分母分式相加减,先通分,变为同分母的分式,再加减.
分式的混合运算顺序:
先算乘方,再算乘除,最后算加减;若有括号,则先算括号里面的;同级运算,按从左到右的顺序进行计算.
负整数指数幂
一般地,当n是正整数时, (a≠0).
这就是说 (a≠0)是 的倒数.
负整数指数幂的三个常用结论:
(1)an与a-n互为倒数;
(3) .
(2) ;
用科学记数法表示小于1的正数
小于1的正数可以用科学记数法表示为a×10-n的形式,其中1≤a<10,n是正整数.
科学记数法是一种记数方法,不改变此数的性质和大小,用科学记数法表示一个负数时,不要忘了前面带“-”号,用科学记数法表示一个带有单位的数时,其表示结果也应带有单位.
1.(1)分式 有意义的条件是__________,值为零的条件是_____.
(2)分式 无意义的条件是______,值为零的条件是____.
x≠1且x≠2
x=±3
x=-2
x=0
重难剖析
2.下列等式从左到右变形一定正确的是( )
C
A. B.
C. D.
没有说明c是否为0
c在等号左边,且在分母上,说明c不为0
3.计算:
解:(1)原式
(1) ;
解:(2)原式
3.计算:
(2) ;
解:(1)原式
4.计算:
(1) ; (2) .
4.计算:
(1) ; (2) .
解:(2)原式
5.用科学记数法表示下列各数:
(1) 0.00001; (2) 0.000000567;
(3) 0.000000301; (4) -0.0023.
解:(1) 0.00001=1×10-5 ;
(2) 0.000000567=5.67×10-7 ;
(3) 0.000000301=3.01×10-7 ;
(4) -0.0023=-2.3×10-3 .
解:(1)原式
能力提升
1.计算:
(1) ; (2) .
解:(2)原式
1.计算:
(1) ; (2) .
解:原式
则不等式组的整数解有-1、0、1、2,
当x=1、-1、0时,原式无意义.
所以x=2,原式=0.
解不等式组得 .
代入原式的值必须使原式有意义.
