湖南省衡阳市第六中学2022-2023学年高二数学学业水平考试阶段性检测习题(二)(含解析)
文档属性
| 名称 | 湖南省衡阳市第六中学2022-2023学年高二数学学业水平考试阶段性检测习题(二)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 159.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-07 00:00:00 | ||
图片预览

文档简介
湖南省衡阳市第六中学2022—2023学年高二数学学业水平考试阶段性检测习题(二)
(时间:80分钟 满分:100分)
一、选择题(本大题共18小题,每小题3分,共54分.每小题列出的四个备选项中只有一个是符合题目要求的,不选、多选、错选均不得分)
1.函数f(x)=的定义域是( )
A.(0,1) B.[0,+∞) C.[1,+∞) D.R
2.5个幂函数:①y=x-2;②y=;③y=;④y=;⑤y=.其中定义域为R的是( )
A.只有①② B.只有②③ C.只有②④ D.只有④⑤
3.函数y=+lg(5-3x)的定义域是( )
A.[0,) B.[0,] C.[1,) D.[1,]
4.方程2x-1+x=5的解所在的区间是( )
A.(0,1) B.(1,2) C.(2,3) D.(3,4)
5.函数f(x)=+a的零点为1,则实数a的值为( )
A.-2 B.- C. D.2
6.函数f(x)=ln(x2-2x-8)的单调递增区间是( )
A.(-∞,-2) B.(-∞,1) C.(1,+∞) D.(4,+∞)
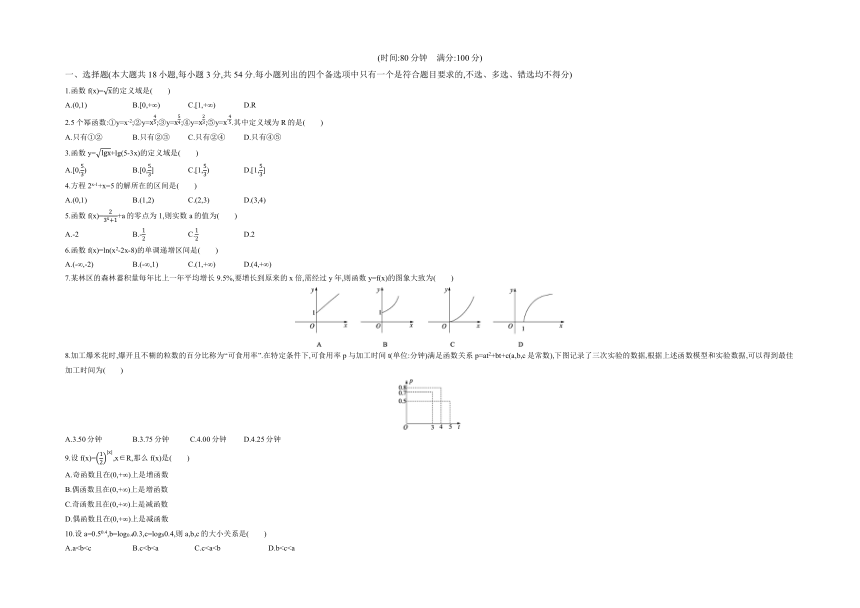
7.某林区的森林蓄积量每年比上一年平均增长9.5%,要增长到原来的x倍,需经过y年,则函数y=f(x)的图象大致为( )
8.加工爆米花时,爆开且不糊的粒数的百分比称为“可食用率”.在特定条件下,可食用率p与加工时间t(单位:分钟)满足函数关系p=at2+bt+c(a,b,c是常数),下图记录了三次实验的数据,根据上述函数模型和实验数据,可以得到最佳加工时间为( )
A.3.50分钟 B.3.75分钟 C.4.00分钟 D.4.25分钟
9.设f(x)=,x∈R,那么f(x)是( )
A.奇函数且在(0,+∞)上是增函数
B.偶函数且在(0,+∞)上是增函数
C.奇函数且在(0,+∞)上是减函数
D.偶函数且在(0,+∞)上是减函数
10.设a=0.50.4,b=log0.40.3,c=log80.4,则a,b,c的大小关系是( )
A.a11.若函数f(x)的图象在R上连续不断,且满足f(0)<0,f(1)>0,f(2)>0,则下列说法正确的是( )
A.f(x)在区间(0,1)上一定有零点,在区间(1,2)上一定没有零点
B.f(x)在区间(0,1)上一定没有零点,在区间(1,2)上一定有零点
C.f(x)在区间(0,1)上一定有零点,在区间(1,2)上可能有零点
D.f(x)在区间(0,1)上可能有零点,在区间(1,2)上一定有零点
12.(2018新课标全国Ⅰ卷)已知函数f(x)=g(x)=f(x)+x+a,若g(x)存在2个零点,则a的取值范围是( )
A.[-1,0) B.[0,+∞)
C.[-1,+∞) D.[1,+∞)
13.函数y=loga(x-1)+1(a>0,a≠1),图象恒过定点A,若点A在一次函数y=mx+n的图象上,其中m>0,n>0,则的最小值是( )
A.6 B.7 C.8 D.9
14.若10x=3,10y=4,则103x-2y=( )
A.-1 B.1 C. D.
15.已知偶函数f(x)在[0,+∞)上单调递增,则对实数a,b,“a>|b|”是“f(a)>f(b)”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
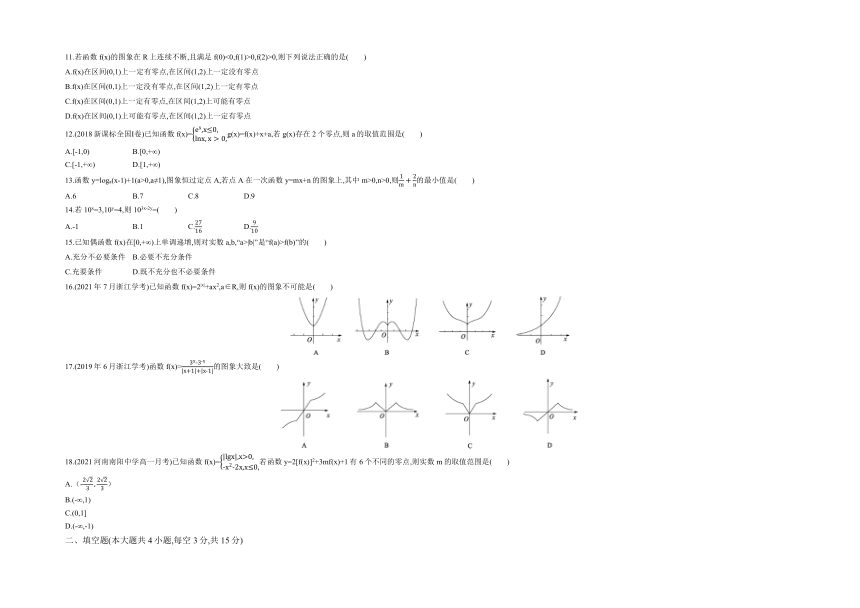
16.(2021年7月浙江学考)已知函数f(x)=2|x|+ax2,a∈R,则f(x)的图象不可能是( )
17.(2019年6月浙江学考)函数f(x)=的图象大致是( )
18.(2021河南南阳中学高一月考)已知函数f(x)=若函数y=2[f(x)]2+3mf(x)+1有6个不同的零点,则实数m的取值范围是( )
A.(-)
B.(-∞,1)
C.(0,1]
D.(-∞,-1)
二、填空题(本大题共4小题,每空3分,共15分)
19.已知幂函数f(x)的图象经过点(4,2),则函数f(x)= ,若f(2-a)>f(a-1),则实数a的取值范围是 .
20.若α∈R,函数f(x)=(x-1)α+3的图象恒过定点P,则点P的坐标为 .
21.若函数f(x)=ax(a>0,a≠1)在[-1,2]上的最大值为4,最小值为m,且函数g(x)=(1-4m)在[0,+∞)上是增函数,则a= .
22.设函数f(x)=(a∈R).若其定义域内不存在实数x,使得f(x)≤0,则a的取值范围是 .
三、解答题(本大题共3小题,共31分)
23.(本小题满分10分)(2021北京北师大二附中高一期中)设f(x)是定义在R上的奇函数,且当x>0时,f(x)=2x+1.
(1)求f(x)的解析式;
(2)若当x<0时,方程f(x)=x2+tx+2t仅有一实根或有两个相等的实根,求实数t的取值范围.
24.(本小题满分10分)已知a>0,b∈R,函数f(x)=ax2+(2a-b)x.
(1)若函数y=f(x)在[-1,1]上有两个不同的零点,求的取值范围;
(2)求证:当x∈[-1,1]时,f(x)≤|2a-b|+a.
25.(本小题满分11分)如图,在直角坐标系xOy中,已知点A(2,0),B(1,),直线x=t(0(1)分别求函数f(t)和g(t)的解析式;
(2)求f(t)的单调递减区间.
参考答案及部分解析
1.B
2.C 解析 ①y=x-2的定义域为(-∞,0)∪(0,+∞),②y=的定义域为R,③y=的定义域为[0,+∞),④y=的定义域为R,⑤y=的定义域为(-∞,0)∪(0,+∞),故选C.
3.C 解析 要使函数有意义,需满足解得1≤x<,则函数的定义域为[1,,)故选C.
4.C 解析 设f(x)=2x-1+x-5,则由指数函数与一次函数的性质可知,函数y=2x-1与y=x-5在R上都是增函数,所以f(x)在R上单调递增,故函数f(x)=2x-1+x-5最多有一个零点,而f(2)=22-1+2-5=-1<0,f(3)=23-1+3-5=2>0,根据函数零点存在定理可知,f(x)=2x-1+x-5有一个零点,且该零点处在区间(2,3)内,故选C.
5.B 解析 函数f(x)=+a的零点为1,所以f(1)=+a=0,解得a=-.故选B.
6.D 解析 由x2-2x-8>0得x∈(-∞,-2)∪(4,+∞),令t=x2-2x-8,则y=ln t,
∵当x∈(-∞,-2)时,t=x2-2x-8单调递减;
当x∈(4,+∞)时,t=x2-2x-8单调递增;又y=ln t为增函数,
故函数f(x)=ln(x2-2x-8)的单调递增区间是(4,+∞),故选D.
7.D 解析 设某林区的森林蓄积量原来为a,依题意知,ax=a(1+9.5%)y,其中x≥1,
所以y=log1.095x(x≥1),故选D.
8.B 解析 由题意可知p=at2+bt+c过点(3,0.7),(4,0.8),(5,0.5),代入p=at2+bt+c中可解得a=-0.2,b=1.5,c=-2,
∴p=-0.2t2+1.5t-2.∴当t=3.75分钟时,可食用率最大.
9.D 解析 因为f(-x)==f(x),所以f(x)为偶函数.又因为当x>0时,f(x)=在(0,+∞)上是减函数,故选D.
10.C 解析 ∵0log0.40.4=1,c=log80.411.C 解析 由题知f(0)·f(1)<0,所以根据函数零点存在定理可得f(x)在区间(0,1)上一定有零点,又f(1)·f(2)>0,因此无法判断f(x)在区间(1,2)上是否有零点.故选C.
12.C 解析 要使得方程g(x)=f(x)+x+a有两个零点,等价于方程f(x)=-x-a有两个实根,即函数y=f(x)的图象与直线y=-x-a的图象有两个交点,从图象可知,-a≤1,即a≥-1.故选C.
13.C 解析 对于函数y=loga(x-1)+1(a>0,a≠1),令x-1=1,求得x=2,y=1,可得函数的图象恒过定点A(2,1),若点A在一次函数y=mx+n的图象上,其中m>0,n>0,则有1=2m+n,则=4+≥4+2=8,当且仅当,即n=2m=时,等号成立,故的最小值是8,故选C.
14.C 解析 依题意,103x-2y=.
故选C.
15.A 解析 因为f(x)是偶函数,所以f(x)=f(|x|).
又因为y=f(x)在[0,+∞)上单调递增,所以f(a)>f(b)等价于f(|a|)>f(|b|),即|a|>|b|.
由a>|b|可得|a|>|b|,但由|a|>|b|无法得到a>|b|.
所以“a>|b|”是“f(a)>f(b)”的充分不必要条件.
16.D 解析 因为f(-x)=f(x),所以函数是偶函数,故D不可能.
17.A 解析 函数的定义域为R,f(-x)==-f(x),故函数f(x)为奇函数,其图象关于原点对称,可排除选项B,C;当x≥1时,f(x)=,x→+∞,f(x)→+∞,故选A.
18.D 解析 令t=f(x),则原函数等价为y=2t2+3mt+1.
作出函数f(x)的图象(图略).
要使关于x的函数y=2[f(x)]2+3mf(x)+1有6个不同的零点,
则函数y=2t2+3mt+1有两个零点t1,t2,
且01或t1=0,t2=1,
令g(t)=2t2+3mt+1,则由根的分布可得,
将t=1,代入得m=-1,
此时g(t)=2t2-3t+1的另一个根为t=,不满足.
若01,则
解得m<-1,故选D.
19. [1,) 解析 设幂函数f(x)=xα,
由f(4)=4α=2,得到α=,
于是f(x)=.
若f(2-a)>f(a-1),
则,
所以
解得1≤a<.
20.(2,4) 解析 因为f(x)=xα过定点(1,1),将图象向右平移一个单位长度,向上平移3个单位长度得f(x)=(x-1)α+3,所以f(x)=(x-1)α+3过定点(2,4).
21. 解析 当a>1时,有a2=4,a-1=m,此时a=2,m=,此时g(x)=-为减函数,不合题意.若022.[0,] 解析 若定义域内不存在实数x,使得f(x)≤0,则f(x)=>0恒成立,则a≥0,a=0时,恒成立,a>0时,>-,当x=-≤-3,即a≤时满足要求.综上得a∈[0,].
23.解 (1)当x<0时,可得-x>0,所以f(-x)=-2x+1.
又因为f(x)是定义在R上的奇函数,所以f(-x)=-f(x),所以f(x)=2x-1.
又由f(0)=0,所以函数的解析式为f(x)=
(2)当x<0时,方程f(x)=x2+tx+2t仅有一实根或有两个相等的实根,
即2x-1=x2+tx+2t仅有一个负根或有两个相等的负实根,
即x2+(t-2)x+2t+1=0仅有一个负根或有两个相等的负实根,
当2t+1<0,即t<-时,方程仅有一个负根,符合题意;
当2t+1=0,即t=-时,方程为x2-x=0,解得x=0或x=,不符合题意;
当2t+1>0,即t>-时,方程的两个根同号,
由Δ=(t-2)2-4(2t+1)=0,解得t=12或t=0,
若t=0,方程为x2-2x+1=(x-1)2=0,解得x=1,不符合题意;
若t=12,方程为x2+10x+25=(x+5)2=0,解得x=-5,符合题意.
综上所述,t=12或t<-,即实数t 的取值范围为-∞,-∪{12}.
24.(1)解 f(x)=ax2+(2a-b)x=0,所以x1=0或x2=,则
即所以∈[1,2)∪(2,3].
(2)证明 因为f(x)=ax2+(2a-b)x,所以f(1)=3a-b,f(-1)=-a+b,f(1)-f(-1)=4a-2b,因为a>0,所以f(x)max=max{f(1),f(-1)}==|2a-b|+a,即f(x)≤|2a-b|+a成立.
25.解 (1)当0当1所以,f(t)=
g(t)=
(2)由(1)中f(t)的解析式可知,函数f(t)的单调递减区间是(1,).
(时间:80分钟 满分:100分)
一、选择题(本大题共18小题,每小题3分,共54分.每小题列出的四个备选项中只有一个是符合题目要求的,不选、多选、错选均不得分)
1.函数f(x)=的定义域是( )
A.(0,1) B.[0,+∞) C.[1,+∞) D.R
2.5个幂函数:①y=x-2;②y=;③y=;④y=;⑤y=.其中定义域为R的是( )
A.只有①② B.只有②③ C.只有②④ D.只有④⑤
3.函数y=+lg(5-3x)的定义域是( )
A.[0,) B.[0,] C.[1,) D.[1,]
4.方程2x-1+x=5的解所在的区间是( )
A.(0,1) B.(1,2) C.(2,3) D.(3,4)
5.函数f(x)=+a的零点为1,则实数a的值为( )
A.-2 B.- C. D.2
6.函数f(x)=ln(x2-2x-8)的单调递增区间是( )
A.(-∞,-2) B.(-∞,1) C.(1,+∞) D.(4,+∞)
7.某林区的森林蓄积量每年比上一年平均增长9.5%,要增长到原来的x倍,需经过y年,则函数y=f(x)的图象大致为( )
8.加工爆米花时,爆开且不糊的粒数的百分比称为“可食用率”.在特定条件下,可食用率p与加工时间t(单位:分钟)满足函数关系p=at2+bt+c(a,b,c是常数),下图记录了三次实验的数据,根据上述函数模型和实验数据,可以得到最佳加工时间为( )
A.3.50分钟 B.3.75分钟 C.4.00分钟 D.4.25分钟
9.设f(x)=,x∈R,那么f(x)是( )
A.奇函数且在(0,+∞)上是增函数
B.偶函数且在(0,+∞)上是增函数
C.奇函数且在(0,+∞)上是减函数
D.偶函数且在(0,+∞)上是减函数
10.设a=0.50.4,b=log0.40.3,c=log80.4,则a,b,c的大小关系是( )
A.a
A.f(x)在区间(0,1)上一定有零点,在区间(1,2)上一定没有零点
B.f(x)在区间(0,1)上一定没有零点,在区间(1,2)上一定有零点
C.f(x)在区间(0,1)上一定有零点,在区间(1,2)上可能有零点
D.f(x)在区间(0,1)上可能有零点,在区间(1,2)上一定有零点
12.(2018新课标全国Ⅰ卷)已知函数f(x)=g(x)=f(x)+x+a,若g(x)存在2个零点,则a的取值范围是( )
A.[-1,0) B.[0,+∞)
C.[-1,+∞) D.[1,+∞)
13.函数y=loga(x-1)+1(a>0,a≠1),图象恒过定点A,若点A在一次函数y=mx+n的图象上,其中m>0,n>0,则的最小值是( )
A.6 B.7 C.8 D.9
14.若10x=3,10y=4,则103x-2y=( )
A.-1 B.1 C. D.
15.已知偶函数f(x)在[0,+∞)上单调递增,则对实数a,b,“a>|b|”是“f(a)>f(b)”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
16.(2021年7月浙江学考)已知函数f(x)=2|x|+ax2,a∈R,则f(x)的图象不可能是( )
17.(2019年6月浙江学考)函数f(x)=的图象大致是( )
18.(2021河南南阳中学高一月考)已知函数f(x)=若函数y=2[f(x)]2+3mf(x)+1有6个不同的零点,则实数m的取值范围是( )
A.(-)
B.(-∞,1)
C.(0,1]
D.(-∞,-1)
二、填空题(本大题共4小题,每空3分,共15分)
19.已知幂函数f(x)的图象经过点(4,2),则函数f(x)= ,若f(2-a)>f(a-1),则实数a的取值范围是 .
20.若α∈R,函数f(x)=(x-1)α+3的图象恒过定点P,则点P的坐标为 .
21.若函数f(x)=ax(a>0,a≠1)在[-1,2]上的最大值为4,最小值为m,且函数g(x)=(1-4m)在[0,+∞)上是增函数,则a= .
22.设函数f(x)=(a∈R).若其定义域内不存在实数x,使得f(x)≤0,则a的取值范围是 .
三、解答题(本大题共3小题,共31分)
23.(本小题满分10分)(2021北京北师大二附中高一期中)设f(x)是定义在R上的奇函数,且当x>0时,f(x)=2x+1.
(1)求f(x)的解析式;
(2)若当x<0时,方程f(x)=x2+tx+2t仅有一实根或有两个相等的实根,求实数t的取值范围.
24.(本小题满分10分)已知a>0,b∈R,函数f(x)=ax2+(2a-b)x.
(1)若函数y=f(x)在[-1,1]上有两个不同的零点,求的取值范围;
(2)求证:当x∈[-1,1]时,f(x)≤|2a-b|+a.
25.(本小题满分11分)如图,在直角坐标系xOy中,已知点A(2,0),B(1,),直线x=t(0
(2)求f(t)的单调递减区间.
参考答案及部分解析
1.B
2.C 解析 ①y=x-2的定义域为(-∞,0)∪(0,+∞),②y=的定义域为R,③y=的定义域为[0,+∞),④y=的定义域为R,⑤y=的定义域为(-∞,0)∪(0,+∞),故选C.
3.C 解析 要使函数有意义,需满足解得1≤x<,则函数的定义域为[1,,)故选C.
4.C 解析 设f(x)=2x-1+x-5,则由指数函数与一次函数的性质可知,函数y=2x-1与y=x-5在R上都是增函数,所以f(x)在R上单调递增,故函数f(x)=2x-1+x-5最多有一个零点,而f(2)=22-1+2-5=-1<0,f(3)=23-1+3-5=2>0,根据函数零点存在定理可知,f(x)=2x-1+x-5有一个零点,且该零点处在区间(2,3)内,故选C.
5.B 解析 函数f(x)=+a的零点为1,所以f(1)=+a=0,解得a=-.故选B.
6.D 解析 由x2-2x-8>0得x∈(-∞,-2)∪(4,+∞),令t=x2-2x-8,则y=ln t,
∵当x∈(-∞,-2)时,t=x2-2x-8单调递减;
当x∈(4,+∞)时,t=x2-2x-8单调递增;又y=ln t为增函数,
故函数f(x)=ln(x2-2x-8)的单调递增区间是(4,+∞),故选D.
7.D 解析 设某林区的森林蓄积量原来为a,依题意知,ax=a(1+9.5%)y,其中x≥1,
所以y=log1.095x(x≥1),故选D.
8.B 解析 由题意可知p=at2+bt+c过点(3,0.7),(4,0.8),(5,0.5),代入p=at2+bt+c中可解得a=-0.2,b=1.5,c=-2,
∴p=-0.2t2+1.5t-2.∴当t=3.75分钟时,可食用率最大.
9.D 解析 因为f(-x)==f(x),所以f(x)为偶函数.又因为当x>0时,f(x)=在(0,+∞)上是减函数,故选D.
10.C 解析 ∵0
12.C 解析 要使得方程g(x)=f(x)+x+a有两个零点,等价于方程f(x)=-x-a有两个实根,即函数y=f(x)的图象与直线y=-x-a的图象有两个交点,从图象可知,-a≤1,即a≥-1.故选C.
13.C 解析 对于函数y=loga(x-1)+1(a>0,a≠1),令x-1=1,求得x=2,y=1,可得函数的图象恒过定点A(2,1),若点A在一次函数y=mx+n的图象上,其中m>0,n>0,则有1=2m+n,则=4+≥4+2=8,当且仅当,即n=2m=时,等号成立,故的最小值是8,故选C.
14.C 解析 依题意,103x-2y=.
故选C.
15.A 解析 因为f(x)是偶函数,所以f(x)=f(|x|).
又因为y=f(x)在[0,+∞)上单调递增,所以f(a)>f(b)等价于f(|a|)>f(|b|),即|a|>|b|.
由a>|b|可得|a|>|b|,但由|a|>|b|无法得到a>|b|.
所以“a>|b|”是“f(a)>f(b)”的充分不必要条件.
16.D 解析 因为f(-x)=f(x),所以函数是偶函数,故D不可能.
17.A 解析 函数的定义域为R,f(-x)==-f(x),故函数f(x)为奇函数,其图象关于原点对称,可排除选项B,C;当x≥1时,f(x)=,x→+∞,f(x)→+∞,故选A.
18.D 解析 令t=f(x),则原函数等价为y=2t2+3mt+1.
作出函数f(x)的图象(图略).
要使关于x的函数y=2[f(x)]2+3mf(x)+1有6个不同的零点,
则函数y=2t2+3mt+1有两个零点t1,t2,
且0
令g(t)=2t2+3mt+1,则由根的分布可得,
将t=1,代入得m=-1,
此时g(t)=2t2-3t+1的另一个根为t=,不满足.
若0
解得m<-1,故选D.
19. [1,) 解析 设幂函数f(x)=xα,
由f(4)=4α=2,得到α=,
于是f(x)=.
若f(2-a)>f(a-1),
则,
所以
解得1≤a<.
20.(2,4) 解析 因为f(x)=xα过定点(1,1),将图象向右平移一个单位长度,向上平移3个单位长度得f(x)=(x-1)α+3,所以f(x)=(x-1)α+3过定点(2,4).
21. 解析 当a>1时,有a2=4,a-1=m,此时a=2,m=,此时g(x)=-为减函数,不合题意.若0
23.解 (1)当x<0时,可得-x>0,所以f(-x)=-2x+1.
又因为f(x)是定义在R上的奇函数,所以f(-x)=-f(x),所以f(x)=2x-1.
又由f(0)=0,所以函数的解析式为f(x)=
(2)当x<0时,方程f(x)=x2+tx+2t仅有一实根或有两个相等的实根,
即2x-1=x2+tx+2t仅有一个负根或有两个相等的负实根,
即x2+(t-2)x+2t+1=0仅有一个负根或有两个相等的负实根,
当2t+1<0,即t<-时,方程仅有一个负根,符合题意;
当2t+1=0,即t=-时,方程为x2-x=0,解得x=0或x=,不符合题意;
当2t+1>0,即t>-时,方程的两个根同号,
由Δ=(t-2)2-4(2t+1)=0,解得t=12或t=0,
若t=0,方程为x2-2x+1=(x-1)2=0,解得x=1,不符合题意;
若t=12,方程为x2+10x+25=(x+5)2=0,解得x=-5,符合题意.
综上所述,t=12或t<-,即实数t 的取值范围为-∞,-∪{12}.
24.(1)解 f(x)=ax2+(2a-b)x=0,所以x1=0或x2=,则
即所以∈[1,2)∪(2,3].
(2)证明 因为f(x)=ax2+(2a-b)x,所以f(1)=3a-b,f(-1)=-a+b,f(1)-f(-1)=4a-2b,因为a>0,所以f(x)max=max{f(1),f(-1)}==|2a-b|+a,即f(x)≤|2a-b|+a成立.
25.解 (1)当0
g(t)=
(2)由(1)中f(t)的解析式可知,函数f(t)的单调递减区间是(1,).
同课章节目录
