弧.弦.圆心角[上学期]

?怤S.ppt(共18张PPT)
圆的对称性及特性
圆是轴对称图形,圆的对称轴是任意一条经过圆心的直线,它有无数条对称轴.
驶向胜利的彼岸
圆也是中心对称图形,它的对称中心就是圆心.
用旋转的方法可以得到:
一个圆绕着它的圆心旋转任意一个角度,都能与原来的图形重合.
这是圆特有的一个性质:圆的旋转不变性
●O
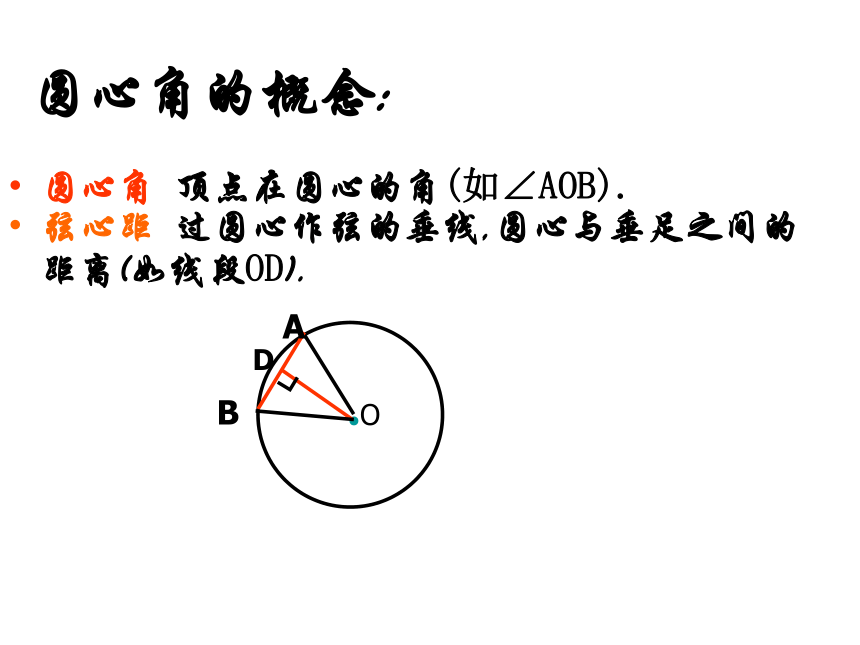
圆心角的概念:
圆心角 顶点在圆心的角(如∠AOB).
弦心距 过圆心作弦的垂线,圆心与垂足之间的距离(如线段OD).
●O
┓
D
A
B
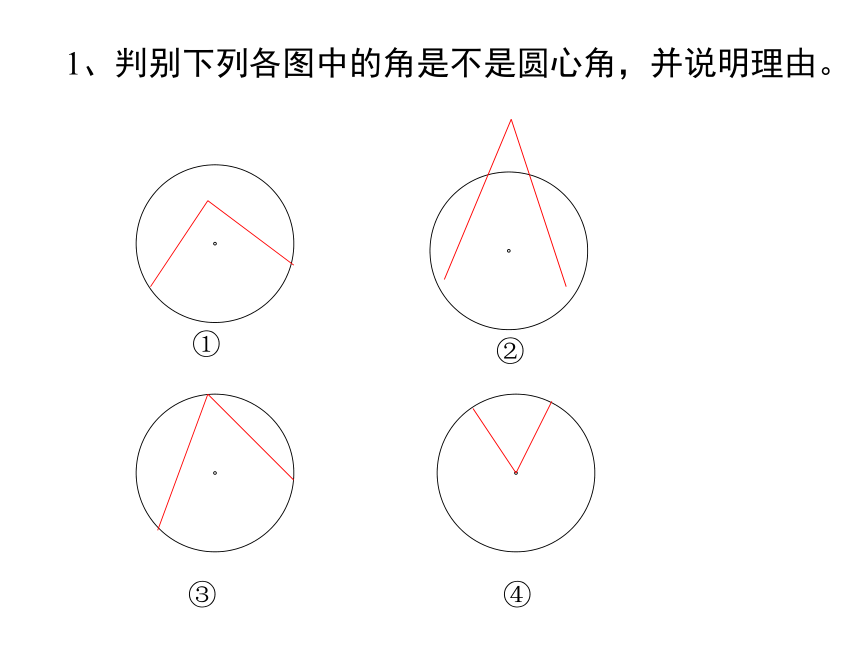
1、判别下列各图中的角是不是圆心角，并说明理由。
①
②
③
④
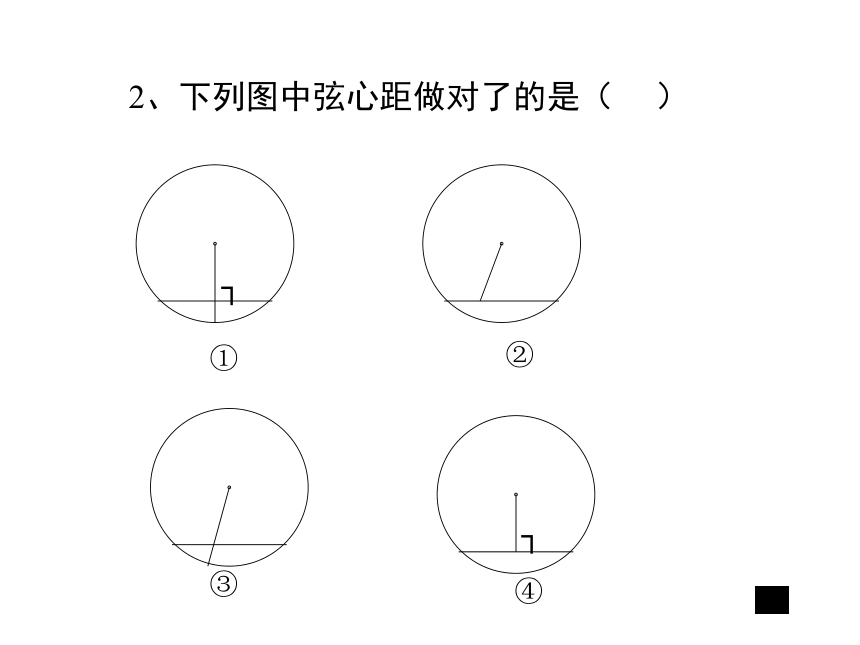
2、下列图中弦心距做对了的是（ ）
┐
┐
①
②
③
④
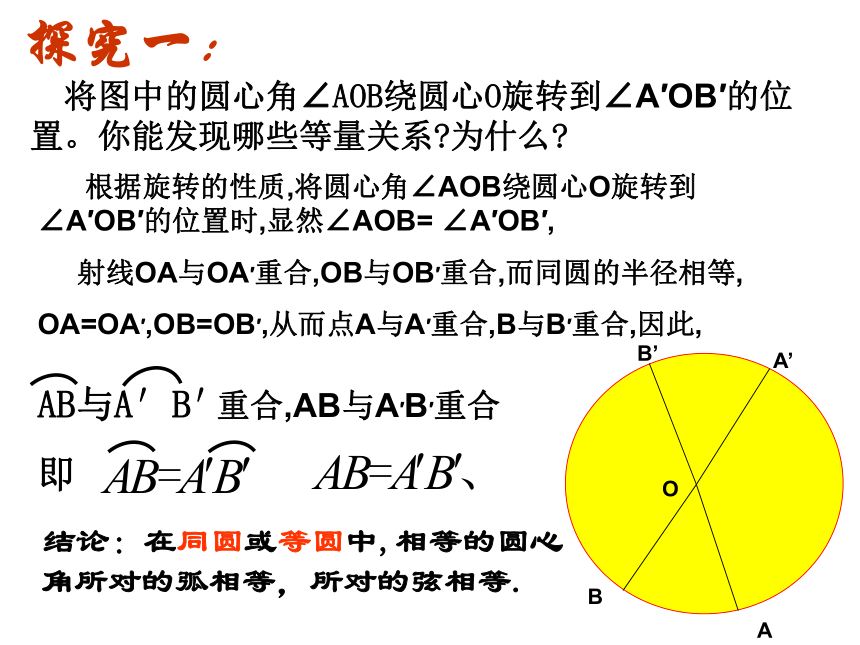
将图中的圆心角∠AOB绕圆心O旋转到∠A′OB′的位置。你能发现哪些等量关系 为什么
探究一：
根据旋转的性质,将圆心角∠AOB绕圆心O旋转到∠A′OB′的位置时,显然∠AOB= ∠A′OB′,
射线OA与OA′重合,OB与OB′重合,而同圆的半径相等,
OA=OA′,OB=OB′,从而点A与A′重合,B与B′重合,因此,
重合,AB与A′B′重合
AB与A′B′
即
结论：在同圆或等圆中,相等的圆心角所对的弧相等，所对的弦相等.
B’
A’
A
B
O
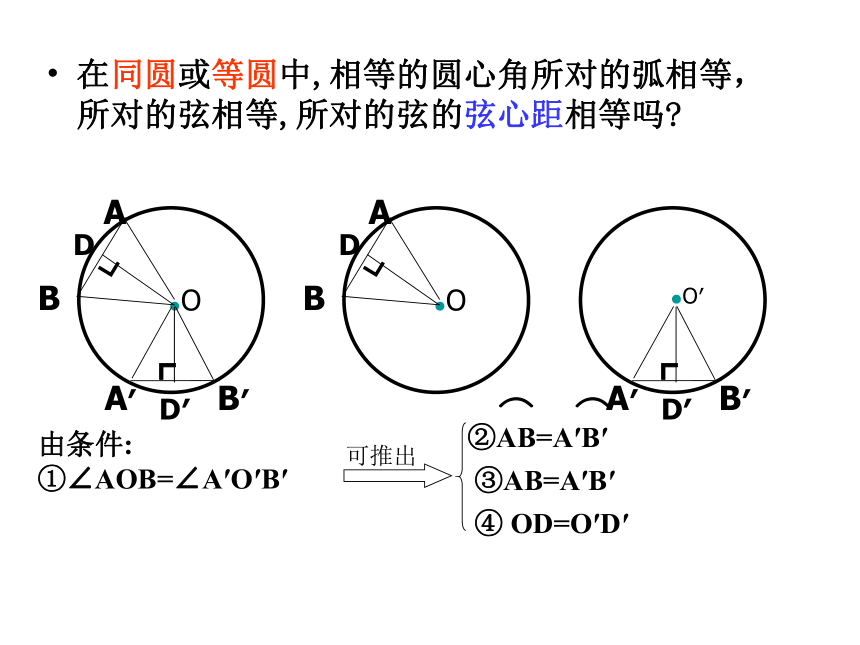
在同圆或等圆中,相等的圆心角所对的弧相等，所对的弦相等,所对的弦的弦心距相等吗
●O
A
B
┓
D
A′
B′
D′
┏
●O
A
B
┓
D
●O′
A′
B′
D′
┏
由条件:
①∠AOB=∠A′O′B′
②AB=A′B′
⌒　⌒
③AB=A′B′
④ OD=O′D′
可推出
在同圆或等圆中,如果轮换下面四组条件:
①两个圆心角,②两条弧,③两条弦,④两条弦心距,你能得出什么结论 与同伴交流你的想法和理由.
●O
A
B
┓
D
A′
B′
D′
┏
●O
A
B
┓
D
●O′
A′
B′
D′
┏
如由条件:
②AB=A′B′
⌒　⌒
③AB=A′B′
④ OD=O′D′
可推出
①∠AOB=∠A′O′B′
推论
在同圆或等圆中,如果①两个圆心角,
②两条弧,③两条弦,④两条弦心距中,
有一组量相等,那么它们所对应的
其余各组量都分别相等.
●O
A
B
┓
D
A′
B′
D′
┏
●O
A
B
┓
D
●O′
A′
B′
D′
┏
如由条件:
②AB=A′B′
⌒　⌒
③AB=A′B′
④ OD=O′D′
可推出
①∠AOB=∠A′O′B′
相等
相等
相等
（或等圆）
2.在同一个圆 中，如果两条弧相等，那么它们所对的圆心角_____、所对的弦______所对的弦的弦心距_____.
结论：
相等
以上四句话如没有在同圆或等圆中，这个结论还会成立吗？
1.在同一个圆 中，如果圆心角相等，那么它所对的弧相等、所对的弦相等,所对的弦的弦心距相等.
（或等圆）
3.在同一个圆 中，如果两条弦相等，那么它们所对的圆心角_____、所对的弧______、所对的弦的弦心距_____. 。
（或等圆）
相等
相等
相等
相等
相等
4.在同一个圆 中，如果两条弦的弦心距相等，那么它们所对的圆心角_____、所对的弧______、所对的弦____ 。
（或等圆）
1、已知：如图，AB、CD是⊙O的两条弦，OE、OF为AB、CD的弦心距，根据本节定理及推论填空：
（1）如果AB=CD，那么
_____________,________,____________。
（2）如果OE=OF，那么
_____________,________,____________。
（3）如果AB=CD 那么
______________,__________,____________。
（4）如果∠AOB=∠COD，那么
_________,________,_________。
⌒
⌒
∠AOB=∠COD OE=OF AB=CD
⌒
⌒
∠AOB=∠COD AB=CD AB=CD
⌒
⌒
∠AOB=∠COD AB=CD OE=OF
OE=OF AB=CD AB=CD
⌒
⌒
2. 如图，在⊙O中， , ∠ACB=60 求 证： ∠AOB= ∠BOC = ∠AOC。
证明： ∵
∴ AB=AC △ABC是等腰三角形
又∠ACB=60
∴ △ABC是等边三角形，AB=BC=CA
∴ ∠AOB= ∠BOC = ∠AOC
A
C
O
B
AB=AC
AB=AC
一.判断下列说法是否正确：
1、相等的圆心角所对的弧相等。（ ）
2、相等的弧所对的弦相等。（ ）
二.如图，⊙O中，AB=CD，
，则
O
D
C
A
B
1
2
试一试你的能力
×
X
50
o
你会做吗？
解：
∵
AC=BD
（已知）
∴
∴
AB=CD
∴
三, 如图，在⊙O中，AC=BD，
,求∠2的度数。
AC-BC=BD-BC
（等式的性质）
∠1=∠2=45°
（在同圆中，相等的弧所对的圆心角相等）
1.如图，在⊙O中，AB＝AC，∠B＝70°.求∠C度数.
2.如图，AB是直径，BC＝CD＝DE，
∠BOC＝40°，求∠AOE的度数
︵
︵
︵
︵
︵
2、如图，点O是∠EPF的平分线上的一点，以O为圆心的圆和角的两边分别交于
点 A、B和C、D。
求证：AB=CD
M
N
证明：作OM⊥AB，ON⊥CD，M，N
为垂足。
推广：若将上题中的点O看作是沿着∠EPF的平分线运动的。
在∠EPF的每边与圆O有两个交点的时候，是否都能够得到上题的结论？
小结:
在同圆或等圆中,如果①两个圆心角,
②两条弧,③两条弦,④两条弦心距中,
有一组量相等,那么它们所对应的
其余各组量都分别相等.
思考题；
司机王师傅这次运输要经过一个如图形状的门楼，已知半圆拱的圆心距地面2M,半径1.5m。王师傅开的是一辆高2.9m，宽2.5m的集装箱卡车，你认为王师傅能通过这个门楼吗？
1.5m
2m