苏教版(2019)必修第一册7.1.2 弧度制 课件(共20张PPT)
文档属性
| 名称 | 苏教版(2019)必修第一册7.1.2 弧度制 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-07 15:45:02 | ||
图片预览








文档简介
(共20张PPT)
第7章
7.1
角与弧度
7.1.1 弧度制
学习目标
1.了解角的另外一种度量方法——弧度制.
2.能进行弧度与角度的互化.
3.掌握弧度制中弧长公式和扇形面积公式.
核心素养:数学抽象 数学运算
新知学习
知识链接 建立弧度制的意义
角的概念推广后,在弧度制下,角的集合与实数集R之间建立起一一对应的关系:每一个角都有唯一的一个实数(等于这个角的弧度数)与它对应;反过来,每一个实数也都有唯一的一个角(即弧度数等于这个实数的角)与它对应
角的集合 实数集R
示例 角度为30°,60°的圆心角,当半径r=1,2,3时.
(1)分别计算相对应的弧长.
(2)分别计算对应弧长与半径之比.
(3)通过(1)(2),你发现圆心角的大小和半径的大小有关系吗?有什么规律?
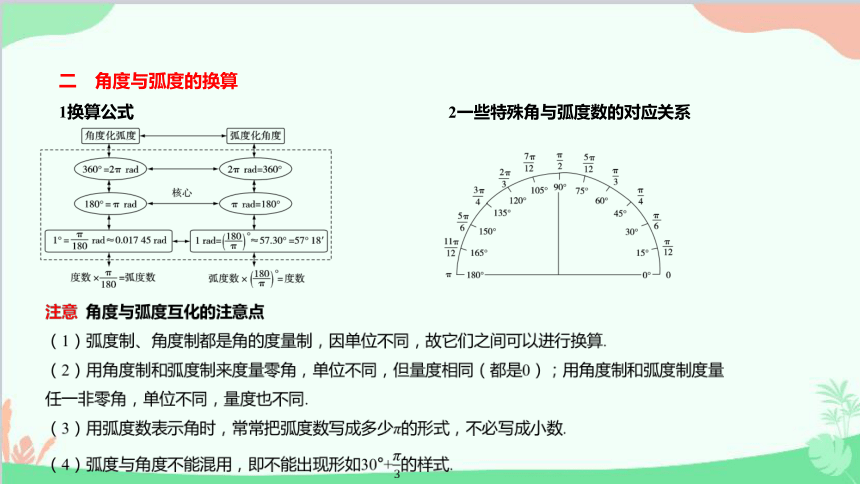
二 角度与弧度的换算
1换算公式
2一些特殊角与弧度数的对应关系
A
三 弧度制下扇形中的弧长公式与面积公式
如图,设圆的半径为r,圆心角为α(0<α<2π),圆心角α所对的弧长为l.
圆心角为α的扇形的面积为S.
3弧长公式及面积公式的两种表示
采用弧度制时,弧长公式和扇形面积公式简单明了,但是要注意使用它们的前提是“弧度制”,若角是以“°”为单位,则应先化为弧度,再利用公式.
弧长与扇形面积公式:
公式 角度制 弧度制
弧长公式 l=|α|r
扇形面积公式
示例 扇形圆心角为216°,半径为25,则该扇形的周长为 ,面积为 .
30π+50
375π
典例剖析
二、用弧度表示终边相同的角
例 2 已知α=1 200°.
(1)将α改写成β+2kπ(k∈Z,0≤β<2π)的形式,并指出α是第几象限的角.
(2)在区间[-4π,π]上找出与角α终边相同的角.
【方法技巧】
在弧度制下,与角α的终边相同的角可以表示为{β|β=2kπ+α,k∈Z},即与角α终边相同的角可以表示成α加上2π的整数倍.
三 扇形的弧长与面积公式的应用
1扇形弧长与面积的计算
例3 已知扇形AOB的周长为8 cm.
(1)若这个扇形的面积为3 cm2,求该扇形的圆心角的大小;
(2)求当这个扇形的面积最大时圆心角的大小和弦AB的长度.
2扇形面积的最值问题
例4 已知扇形的圆心角是α(α>0),半径是r,弧长为l.
(1)若α=100°,r=2,求扇形的面积;
(2)若扇形的周长为20,求扇形面积的最大值,并求此时扇形圆心角的弧度数.
方法技巧
解决扇形的面积的最值问题,一般思路是利用扇形的面积公式建立起目标函数,然后利用
二次函数或基本不等式求最值.
四 与弧度有关的实际应用问题
例 5 某单位拟建一个扇环面形状的花坛(如图7-1-23所示),该扇环面由以点O为圆心的两个同心圆弧和延长后通过点O的两条线段围成.按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为x米,圆心角(正角)为θ(弧度).
(1)求θ关于x的函数关系式.
(2)已知在花坛的边缘(实线部分)进行装饰时,直线部分的装饰费用为4元/米,弧线部分的装饰费用为9元/米.设花坛的面积与装饰总费用的比为y,求y关于x的函数关系式,并求出x为何值时,y取得最大值?
C
随堂小测
C
D
5. 已知集合A={x|2kπ≤x≤2kπ+π, k∈Z},集合B={x|-46. 某镇要修建一个扇形绿化区域,其周长为400 m,所在圆的半径为r m,扇形的圆心角的弧度数为θ,θ∈(0,2π).
(1)求绿化区域面积S(m2)关于r(m)的函数关系式,并指出r的取值范围.
(2)所在圆的半径r取何值时,才能使绿化区域的面积S最大?求出最大值.
(-4,-π]∪[0,π]
谢 谢!
第7章
7.1
角与弧度
7.1.1 弧度制
学习目标
1.了解角的另外一种度量方法——弧度制.
2.能进行弧度与角度的互化.
3.掌握弧度制中弧长公式和扇形面积公式.
核心素养:数学抽象 数学运算
新知学习
知识链接 建立弧度制的意义
角的概念推广后,在弧度制下,角的集合与实数集R之间建立起一一对应的关系:每一个角都有唯一的一个实数(等于这个角的弧度数)与它对应;反过来,每一个实数也都有唯一的一个角(即弧度数等于这个实数的角)与它对应
角的集合 实数集R
示例 角度为30°,60°的圆心角,当半径r=1,2,3时.
(1)分别计算相对应的弧长.
(2)分别计算对应弧长与半径之比.
(3)通过(1)(2),你发现圆心角的大小和半径的大小有关系吗?有什么规律?
二 角度与弧度的换算
1换算公式
2一些特殊角与弧度数的对应关系
A
三 弧度制下扇形中的弧长公式与面积公式
如图,设圆的半径为r,圆心角为α(0<α<2π),圆心角α所对的弧长为l.
圆心角为α的扇形的面积为S.
3弧长公式及面积公式的两种表示
采用弧度制时,弧长公式和扇形面积公式简单明了,但是要注意使用它们的前提是“弧度制”,若角是以“°”为单位,则应先化为弧度,再利用公式.
弧长与扇形面积公式:
公式 角度制 弧度制
弧长公式 l=|α|r
扇形面积公式
示例 扇形圆心角为216°,半径为25,则该扇形的周长为 ,面积为 .
30π+50
375π
典例剖析
二、用弧度表示终边相同的角
例 2 已知α=1 200°.
(1)将α改写成β+2kπ(k∈Z,0≤β<2π)的形式,并指出α是第几象限的角.
(2)在区间[-4π,π]上找出与角α终边相同的角.
【方法技巧】
在弧度制下,与角α的终边相同的角可以表示为{β|β=2kπ+α,k∈Z},即与角α终边相同的角可以表示成α加上2π的整数倍.
三 扇形的弧长与面积公式的应用
1扇形弧长与面积的计算
例3 已知扇形AOB的周长为8 cm.
(1)若这个扇形的面积为3 cm2,求该扇形的圆心角的大小;
(2)求当这个扇形的面积最大时圆心角的大小和弦AB的长度.
2扇形面积的最值问题
例4 已知扇形的圆心角是α(α>0),半径是r,弧长为l.
(1)若α=100°,r=2,求扇形的面积;
(2)若扇形的周长为20,求扇形面积的最大值,并求此时扇形圆心角的弧度数.
方法技巧
解决扇形的面积的最值问题,一般思路是利用扇形的面积公式建立起目标函数,然后利用
二次函数或基本不等式求最值.
四 与弧度有关的实际应用问题
例 5 某单位拟建一个扇环面形状的花坛(如图7-1-23所示),该扇环面由以点O为圆心的两个同心圆弧和延长后通过点O的两条线段围成.按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为x米,圆心角(正角)为θ(弧度).
(1)求θ关于x的函数关系式.
(2)已知在花坛的边缘(实线部分)进行装饰时,直线部分的装饰费用为4元/米,弧线部分的装饰费用为9元/米.设花坛的面积与装饰总费用的比为y,求y关于x的函数关系式,并求出x为何值时,y取得最大值?
C
随堂小测
C
D
5. 已知集合A={x|2kπ≤x≤2kπ+π, k∈Z},集合B={x|-4
(1)求绿化区域面积S(m2)关于r(m)的函数关系式,并指出r的取值范围.
(2)所在圆的半径r取何值时,才能使绿化区域的面积S最大?求出最大值.
(-4,-π]∪[0,π]
谢 谢!
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
