数学人教A版(2019)必修第一册3.3 幂函数 课件(共23张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册3.3 幂函数 课件(共23张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 948.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-07 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
空白演示
单击输入您的封面副标题
3.3 幂函数
第三章 函数的概念与性质
学习新知
(1)如果张红以1元/kg的价格购买了某种蔬菜wkg,那么她需要支付p=____元;
(2)如果正方形的边长为a,那么正方形的面积S=____;
(3)如果立方体的棱长为b,那么立方体的体积V=____;
(4)如果一个正方形场地的面积为S,那么这个正方形的边长c=____;
(5)如果某人ts内骑车行进了1km,那么他骑车的平均速度v=_____.
w
a2
b3
这些函数解析式有什么共同特征?
幂函数
定义:一般地,函数叫做幂函数,
其中x是自变量,是常数.
特征:
①底数:自变量x
②指数:常数
③系数:1
高中阶段主要研究这5个幂函数:
例题讲解---题型一幂函数的概念
例1 下列哪些函数是幂函数
①y=x3;
②y=2x;
③y=4x2;
④y=x5+1;
⑤y=(x-1)2;
⑥y=x;
⑦y=x-2
√
√
√
×
×
×
×
例2 若y=mxα+(2n-4)是幂函数,则m+n=________.
解析:因为y=mxα+(2n-4)是幂函数,所以m=1,2n-4=0,即m=1,n=2.所以m+n=3.
答案:3
例题讲解---题型一幂函数的概念
例3 (多选)已知幂函数的图象不过原点,则实数m的取值可以为( )
A.5 B.1 C.2 D.4
BC
例题讲解---题型一幂函数的概念
答案:81
习题演练
2函数是幂函数,且当时,是增函数,试确定m的值.
习题演练
学习新知
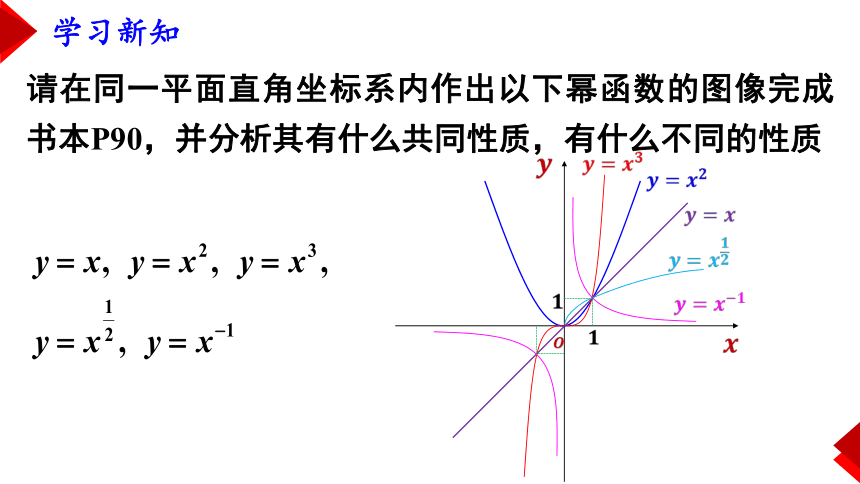
请在同一平面直角坐标系内作出以下幂函数的图像完成书本P90,并分析其有什么共同性质,有什么不同的性质
幂函数的图像与性质
1.函数解析式:
2.定点:
当α>0时,图象都过原点
所有的幂函数在(0,+∞)都有定义,
图象都过点(1,1)
3.单调性:
当α>0时,幂函数在[0,+∞)上单调递增;
当α<0时,幂函数在(0,+∞)上单调递减
4.奇偶性:
当α为奇数时,幂函数为奇函数,
当α为偶数时,幂函数为偶函数
幂函数的图像与性质
5.图象的高低:
幂函数的图象在(1,+∞)上指数越大,
图象越高(指大图高)
例题讲解---题型二幂函数的性质
例4
B
例题讲解---题型二幂函数的性质
例4 (2)如图所示,C1,C2,C3为幂函数y=xα在第一象限内的图象,则解析式中的指数α依次可以取( )
C
例题讲解---题型三比较大小
例题讲解---题型三比较大小
例题讲解---题型三比较大小
归纳小结
习题演练
例5已知幂函数y=x3m-9(m∈N*)的图象关于y轴对称,且在(0,+∞)上是减函数.(1)求m的值;(2)求满足不等式<的实数a的取值范围.
例题讲解---题型四解不等式
解:(1)因为幂函数y=x3m-9在(0,+∞)上是减函数,
所以3m-9<0,所以m<3,
因为m∈N*,所以m=1或2,
又因为函数图象关于y轴对称,
所以3m-9是偶数,所以m=1.
例题讲解---题型四解不等式
例5已知幂函数y=x3m-9(m∈N*)的图象关于y轴对称,且在(0,+∞)上是减函数.
(2)求满足不等式<的实数a的取值范围.
习题演练
习题演练
利用幂函数的性质解不等式的步骤
(1)确定可以利用的幂函数;
(2)借助相应的幂函数的单调性,将不等式的大小关系转化为自变量的大小关系;
(3)解不等式(组)求参数范围时,注意分类讨论思想的应用.
归纳小结
空白演示
单击输入您的封面副标题
3.3 幂函数
第三章 函数的概念与性质
学习新知
(1)如果张红以1元/kg的价格购买了某种蔬菜wkg,那么她需要支付p=____元;
(2)如果正方形的边长为a,那么正方形的面积S=____;
(3)如果立方体的棱长为b,那么立方体的体积V=____;
(4)如果一个正方形场地的面积为S,那么这个正方形的边长c=____;
(5)如果某人ts内骑车行进了1km,那么他骑车的平均速度v=_____.
w
a2
b3
这些函数解析式有什么共同特征?
幂函数
定义:一般地,函数叫做幂函数,
其中x是自变量,是常数.
特征:
①底数:自变量x
②指数:常数
③系数:1
高中阶段主要研究这5个幂函数:
例题讲解---题型一幂函数的概念
例1 下列哪些函数是幂函数
①y=x3;
②y=2x;
③y=4x2;
④y=x5+1;
⑤y=(x-1)2;
⑥y=x;
⑦y=x-2
√
√
√
×
×
×
×
例2 若y=mxα+(2n-4)是幂函数,则m+n=________.
解析:因为y=mxα+(2n-4)是幂函数,所以m=1,2n-4=0,即m=1,n=2.所以m+n=3.
答案:3
例题讲解---题型一幂函数的概念
例3 (多选)已知幂函数的图象不过原点,则实数m的取值可以为( )
A.5 B.1 C.2 D.4
BC
例题讲解---题型一幂函数的概念
答案:81
习题演练
2函数是幂函数,且当时,是增函数,试确定m的值.
习题演练
学习新知
请在同一平面直角坐标系内作出以下幂函数的图像完成书本P90,并分析其有什么共同性质,有什么不同的性质
幂函数的图像与性质
1.函数解析式:
2.定点:
当α>0时,图象都过原点
所有的幂函数在(0,+∞)都有定义,
图象都过点(1,1)
3.单调性:
当α>0时,幂函数在[0,+∞)上单调递增;
当α<0时,幂函数在(0,+∞)上单调递减
4.奇偶性:
当α为奇数时,幂函数为奇函数,
当α为偶数时,幂函数为偶函数
幂函数的图像与性质
5.图象的高低:
幂函数的图象在(1,+∞)上指数越大,
图象越高(指大图高)
例题讲解---题型二幂函数的性质
例4
B
例题讲解---题型二幂函数的性质
例4 (2)如图所示,C1,C2,C3为幂函数y=xα在第一象限内的图象,则解析式中的指数α依次可以取( )
C
例题讲解---题型三比较大小
例题讲解---题型三比较大小
例题讲解---题型三比较大小
归纳小结
习题演练
例5已知幂函数y=x3m-9(m∈N*)的图象关于y轴对称,且在(0,+∞)上是减函数.(1)求m的值;(2)求满足不等式<的实数a的取值范围.
例题讲解---题型四解不等式
解:(1)因为幂函数y=x3m-9在(0,+∞)上是减函数,
所以3m-9<0,所以m<3,
因为m∈N*,所以m=1或2,
又因为函数图象关于y轴对称,
所以3m-9是偶数,所以m=1.
例题讲解---题型四解不等式
例5已知幂函数y=x3m-9(m∈N*)的图象关于y轴对称,且在(0,+∞)上是减函数.
(2)求满足不等式<的实数a的取值范围.
习题演练
习题演练
利用幂函数的性质解不等式的步骤
(1)确定可以利用的幂函数;
(2)借助相应的幂函数的单调性,将不等式的大小关系转化为自变量的大小关系;
(3)解不等式(组)求参数范围时,注意分类讨论思想的应用.
归纳小结
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
