圆周角[上学期]

课件14张PPT。圆周角复习提问：
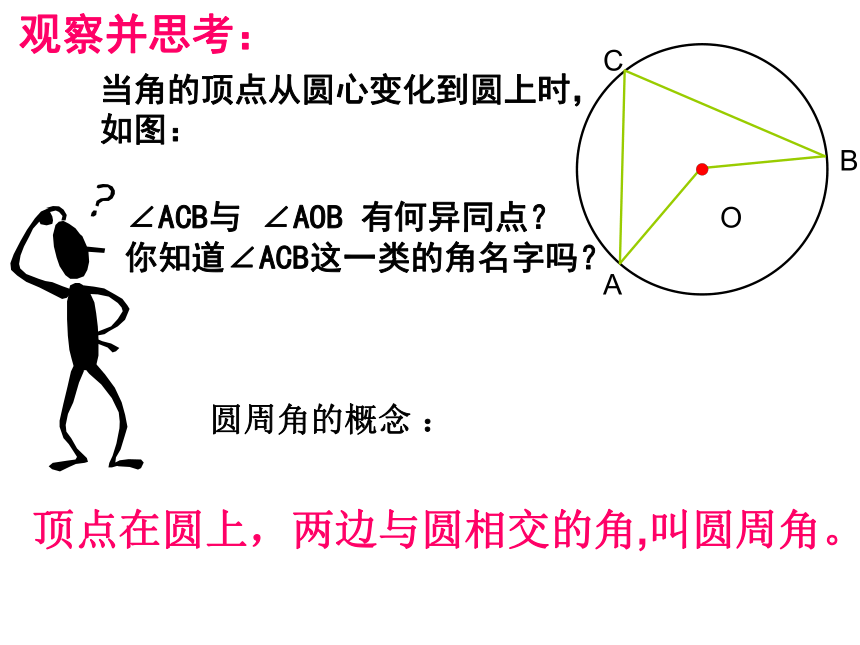
（1）什么是圆心角？ （2）圆心角，弧，弦，弦心距关系定理是什么？ ∠ACB与 ∠AOB 有何异同点？
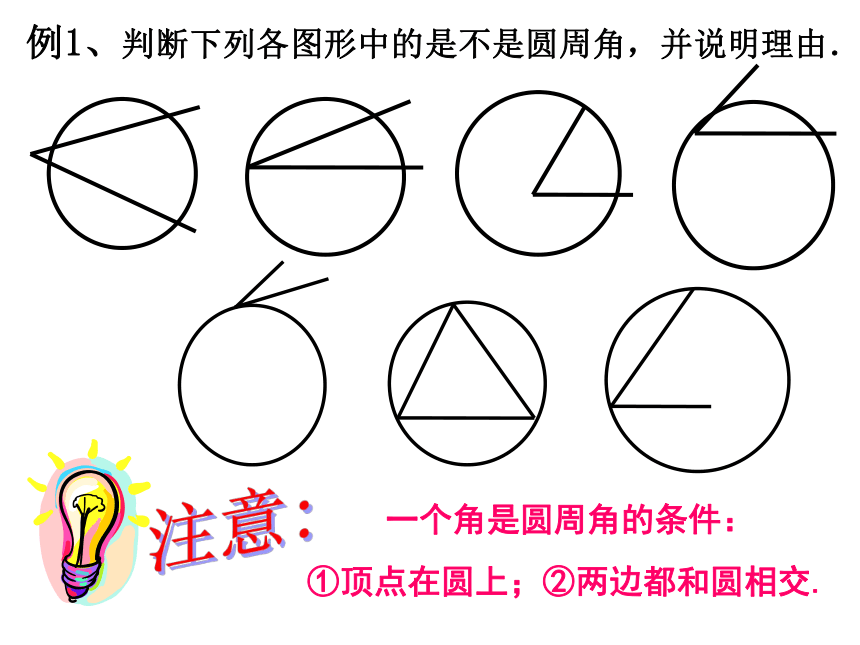
你知道∠ACB这一类的角名字吗？ 顶点在圆上，两边与圆相交的角,叫圆周角。 圆周角的概念 ： 当角的顶点从圆心变化到圆上时，如图：观察并思考：例1、判断下列各图形中的是不是圆周角，并说明理由． 一个角是圆周角的条件：
①顶点在圆上；②两边都和圆相交.
注意: 想一想？ 圆周角的度数与相应的圆心角度数有
什么关系？
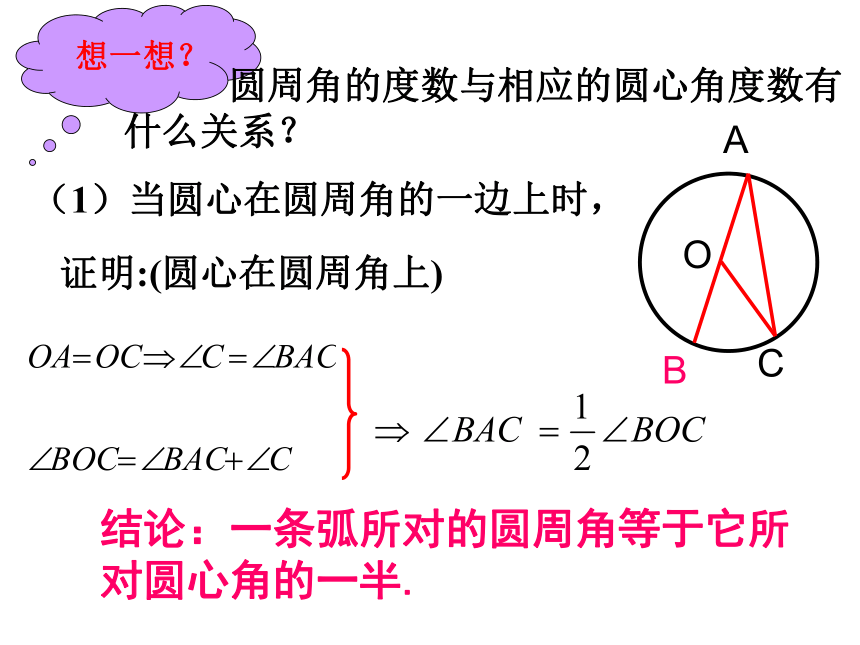
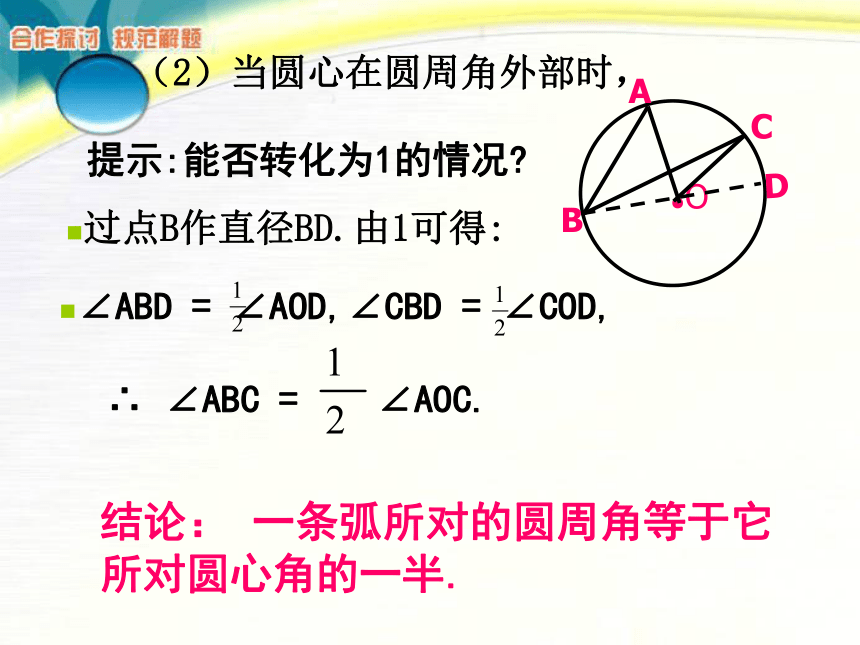
（1）当圆心在圆周角的一边上时，证明:(圆心在圆周角上) 结论：一条弧所对的圆周角等于它所对圆心角的一半.COBA（2）当圆心在圆周角外部时，
结论： 一条弧所对的圆周角等于它所对圆心角的一半. 提示:能否转化为1的情况?过点B作直径BD.由1可得: ∴ ∠ABC = ∠AOC.∠ABD = ∠AOD,∠CBD = ∠COD,D（3）当圆心在圆周角内部时，
提示:能否转化为1的情况?过点B作直径BD.由1可得: ∴ ∠ABC = ∠AOC.∠ABD = ∠AOD,∠CBD = ∠COD,结论： 一条弧所对的圆周角等于它
所对圆心角的一半. 圆周角定理在同圆或等圆中，同弧或等弧所对的圆周角等于它所对圆心角的一半.例2、如图,在⊙O中,∠BOC =50°,
求∠A的大小.例3、如图，∠A是圆O的圆周角， ∠A=40°，求∠OBC的度数。 例4、如图7—96、OA、OB、OC都是⊙O的半径，∠AOB=2∠BOC．
求证：∠ABC=∠BAC．练习：
已知：△ABC的三个顶点在⊙O上，∠BAC=50°，∠ABC=47°，求∠AOB．
解：有题意知：∠A、∠B、∠C是圆周角，
∠AOB是圆心角．　
又∵∠BAC=50°，∠ABC=47°　∴∠ACB=180°-(∠A＋∠B)
=180°-(50°＋47°)
=83°．∴ ∠AOB＝2∠ACB＝2×83°＝166°． 本节课你学到了什么？有什么收获呢？课堂小结：思考：圆周角定理能不能理解成： “一条弧所对的圆心角等于它所对的 圆周角的二倍．”？
书上P94
3题、4题、8题、9题
《轻巧夺冠》课后作业：