圆的复习[上学期]
图片预览
文档简介
与圆有关的位置关系
1圆的有关概念:
掌握弦和直径之间的关系,什么是等弧,
2.垂径定理概念与规律:
圆是轴对称图形,任何经过圆形的直线都是它的对称轴。
垂直于弦的直径平分弦,并且平分弦所对的两条弧。
在圆中,解有关弦的问题时,常作“垂直于弦”的直径或半径,但往往只作出圆心到弦的垂线段作为辅助线。
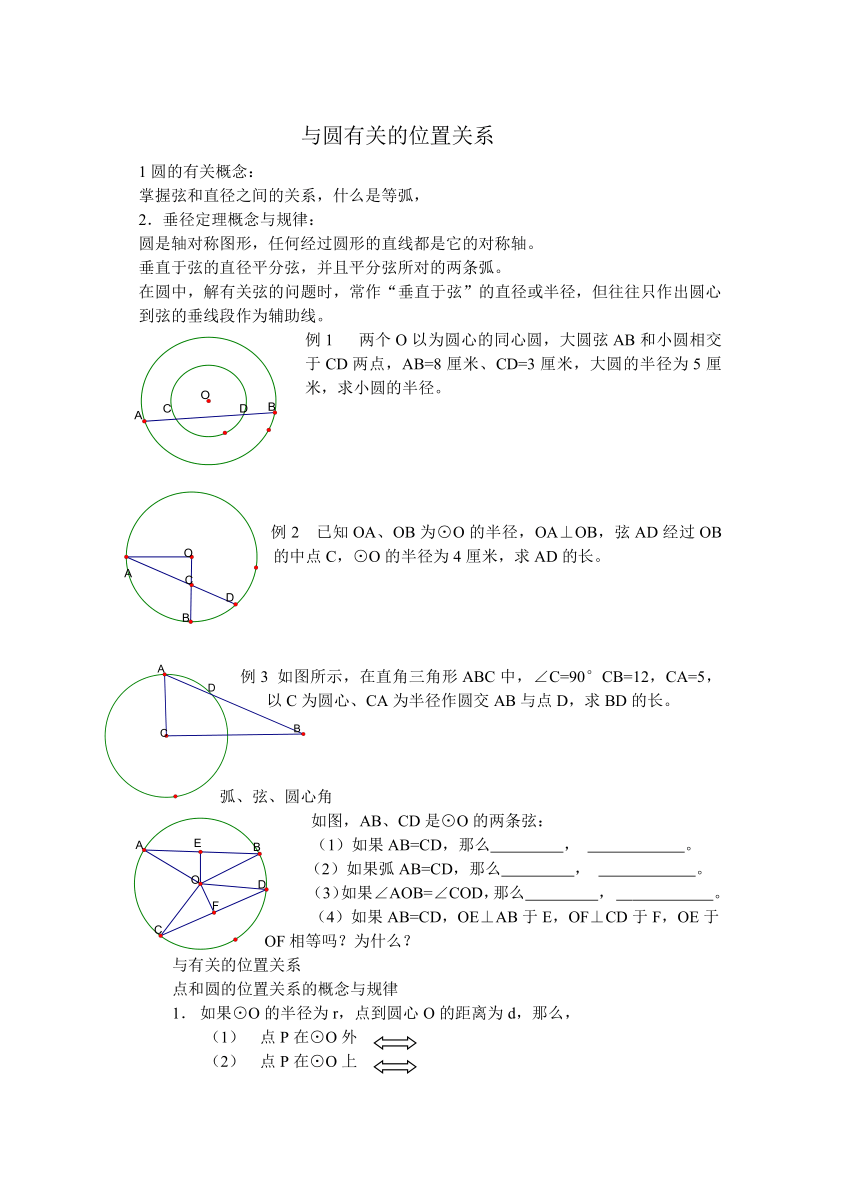
例1 两个O以为圆心的同心圆,大圆弦AB和小圆相交于CD两点,AB=8厘米、CD=3厘米,大圆的半径为5厘米,求小圆的半径。
例2 已知OA、OB为⊙O的半径,OA⊥OB,弦AD经过OB的中点C,⊙O的半径为4厘米,求AD的长。
例3 如图所示,在直角三角形ABC中,∠C=90°CB=12,CA=5,以C为圆心、CA为半径作圆交AB与点D,求BD的长。
弧、弦、圆心角
如图,AB、CD是⊙O的两条弦:
(1)如果AB=CD,那么 , 。
(2)如果弧AB=CD,那么 , 。
(3)如果∠AOB=∠COD,那么 , 。
(4)如果AB=CD,OE⊥AB于E,OF⊥CD于F,OE于OF相等吗?为什么?
与有关的位置关系
点和圆的位置关系的概念与规律
1. 如果⊙O的半径为r,点到圆心O的距离为d,那么,
(1) 点P在⊙O外
(2) 点P在⊙O上
(3) 点P在⊙O内
例题 1
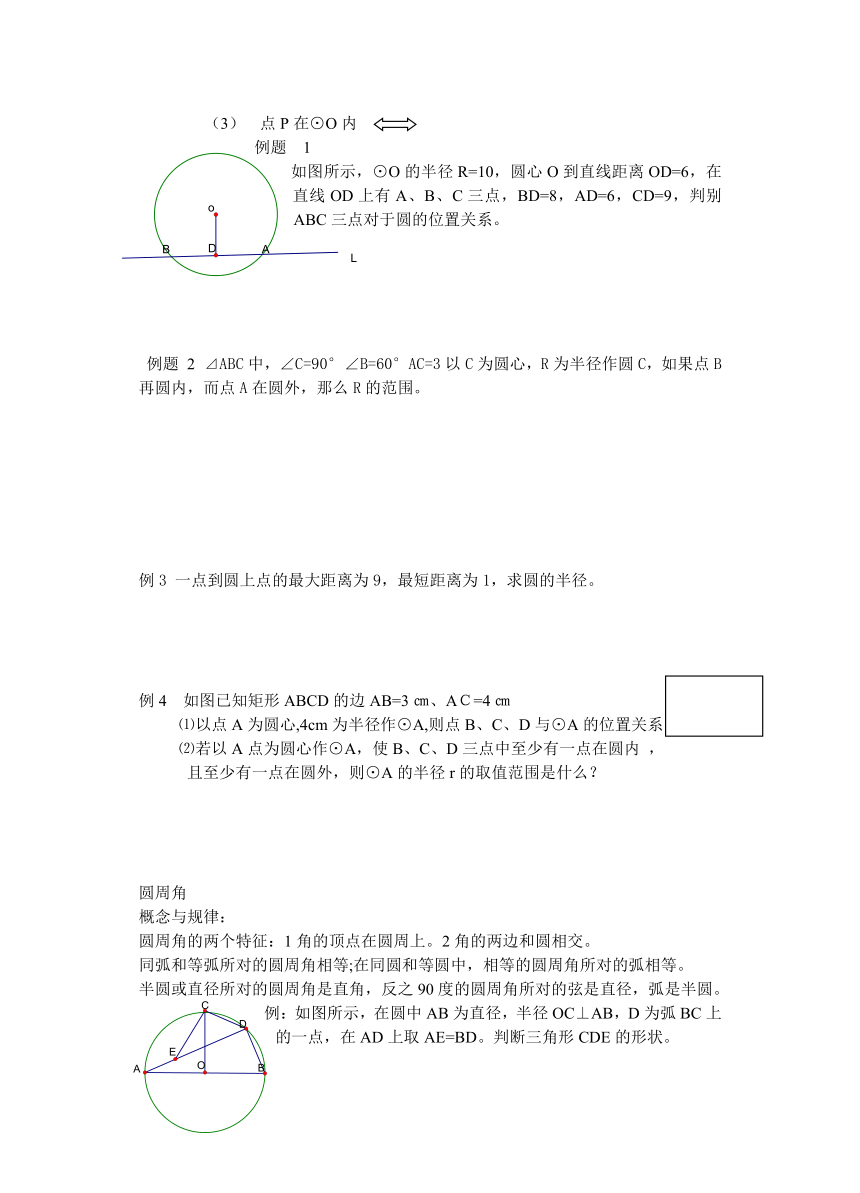
如图所示,⊙O的半径R=10,圆心O到直线距离OD=6,在直线OD上有A、B、C三点,BD=8,AD=6,CD=9,判别ABC三点对于圆的位置关系。
例题 2 ⊿ABC中,∠C=90°∠B=60°AC=3以C为圆心,R为半径作圆C,如果点B再圆内,而点A在圆外,那么R的范围。
例3 一点到圆上点的最大距离为9,最短距离为1,求圆的半径。
例4 如图已知矩形ABCD的边AB=3㎝、AC=4㎝
⑴以点A为圆心,4cm为半径作⊙A,则点B、C、D与⊙A的位置关系
⑵若以A点为圆心作⊙A,使B、C、D三点中至少有一点在圆内 ,
且至少有一点在圆外,则⊙A的半径r的取值范围是什么?
圆周角
概念与规律:
圆周角的两个特征:1角的顶点在圆周上。2角的两边和圆相交。
同弧和等弧所对的圆周角相等;在同圆和等圆中,相等的圆周角所对的弧相等。
半圆或直径所对的圆周角是直角,反之90度的圆周角所对的弦是直径,弧是半圆。
例:如图所示,在圆中AB为直径,半径OC⊥AB,D为弧BC上的一点,在AD上取AE=BD。判断三角形CDE的形状。
直线和圆的位置关系
概念与规律
1. 直线与圆的位置关系有三种情况:
(1) 相离----直线与圆没有公共点,此时直线到圆心的距离大于半径。
(2) 相切-----直线与圆只有一个公共点,此时直线到圆心的距离等于半径。
(3) 相交-----直线与圆有两个公共点,此时直线到圆心的距离小于半径。
例1已知⊙A的直径为6,A点坐标是(-3,-4),则⊙A与x轴的位置关系如何?与y轴的位置关系如何?
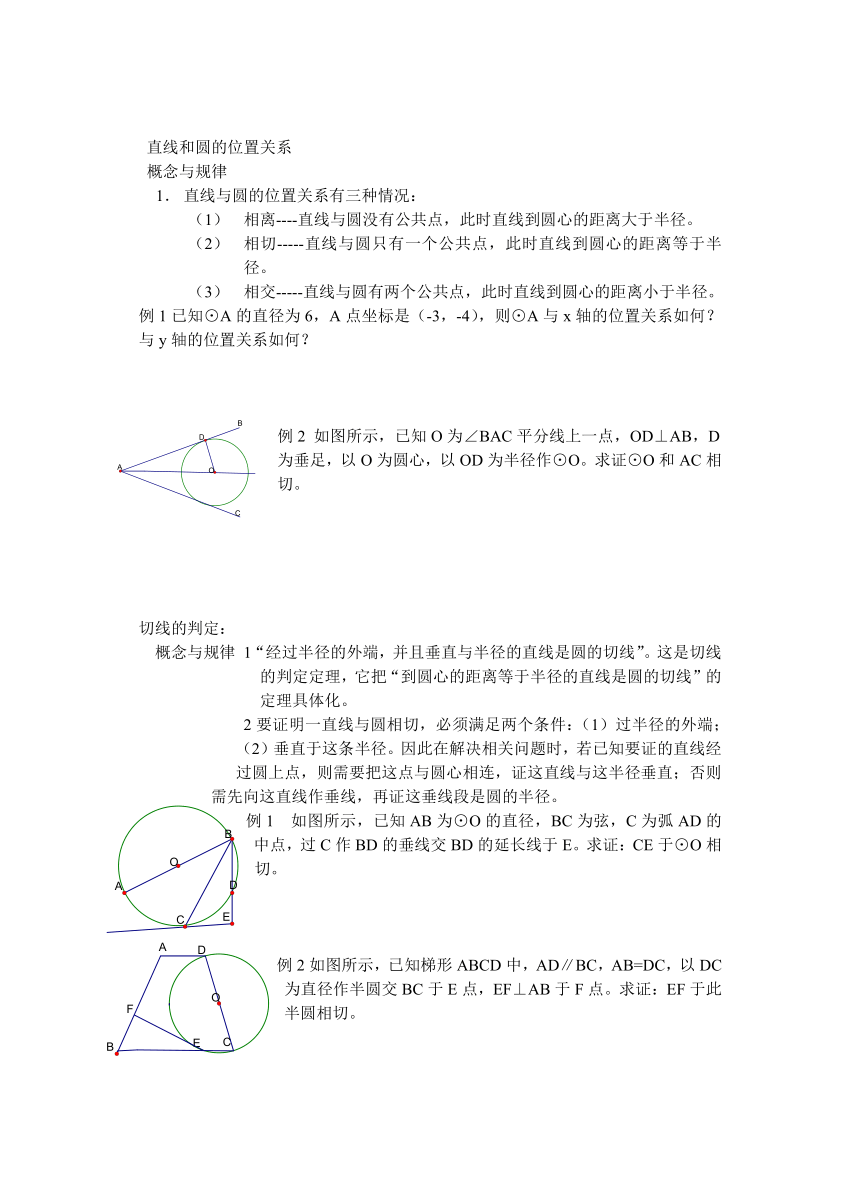
例2 如图所示,已知O为∠BAC平分线上一点,OD⊥AB,D为垂足,以O为圆心,以OD为半径作⊙O。求证⊙O和AC相切。
切线的判定:
概念与规律 1“经过半径的外端,并且垂直与半径的直线是圆的切线”。这是切线的判定定理,它把“到圆心的距离等于半径的直线是圆的切线”的定理具体化。
2要证明一直线与圆相切,必须满足两个条件:(1)过半径的外端;(2)垂直于这条半径。因此在解决相关问题时,若已知要证的直线经过圆上点,则需要把这点与圆心相连,证这直线与这半径垂直;否则需先向这直线作垂线,再证这垂线段是圆的半径。
例1 如图所示,已知AB为⊙O的直径,BC为弦,C为弧AD的中点,过C作BD的垂线交BD的延长线于E。求证:CE于⊙O相切。
例2如图所示,已知梯形ABCD中,AD∥BC,AB=DC,以DC为直径作半圆交BC于E点,EF⊥AB于F点。求证:EF于此半圆相切。
切线的性质
圆的切线垂直经过切点的半径。因此在解关于切线的问题中,通常把过切点的半径连接起来,得到90度的角。
例1如图所示已知在⊿ABC中,AB为⊙O的直径,⊙O交AB于D 点,过D点作圆的切线交BC于E点,且BE=DE。求证;BC于⊙O相切。
例2如图所示,已知AB切⊙O于E点,CD切⊙O于F点,AB∥CD,OA⊥OC,求证AC与⊙O相切。
例3 如图所示,半径为2的⊙P的圆心在直线y=2x-1上运动。
(1) 当⊙P与y轴相切时,写出P点坐标。
(2) 当⊙P与x 轴相切时,写出P点坐标。
(3) ⊙P是否能同时与x轴、y轴相切,若能,写出P点坐标,若不能请说明理由。
例4如图所示,点在⊙O直径AB 延长线上的一点,CD切⊙O于D,且DC=DA=4,CE⊥AD,交AD的延长线于E。求DE的长。
三角形的内切圆、切线长定理;
内心的性质:内心到各边的距离相等,内心与各顶点的连线构成角平分线。
三角形的内心与一边两个端点连线的夹角等于90度与第三个内角一半的和。
切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,该点与圆心的连线平分两条切线的夹角。
例1 如图,已知直角三角形ABC,∠ACB=90°I为它的内心,∠BIC=105°,AC=,求各边长及内切圆的半径。
例2 已知直角梯形ABCD中,AD∥BC,∠B=90°以AB为直径作⊙O切CD于E点。求证:OD⊥OC;若AD=9,BC=16,求梯形的周长和面积。
圆和圆的位置关系
两圆的位置关系是由半径和、差与圆心距的大小关系判定的:
d > r+R
d = r+R
R-r<d < r+R
d = R-r
d < R-r
1、⊙O1、⊙O2的半径分别为40mm和25mm,两圆相交于A、B两点。若AB=48mm,则O1O2= mm。
2、已知⊙O1与⊙O2相切,它们的半径分别为3和6,则圆心距O1O2的长为 。
3、现有半径分别为5mm和4mm的两种钢球各2个,技术员小张用它们来测量一些口小内大的机器零件的内孔直径。
(1)如图示(此图为截面示意图),小张用上述两种钢球各一个进行测量时,测得钢球顶点与孔口平面的距离分别为11mm、10mm,则此零件的内孔直径是多少?
4、在平面直角坐标系中,⊙O1与⊙O2外切,它们的半径分别为6和4。若
圆心O1的坐标为(8,0),圆心O2在坐标轴上,则点O2的坐标为 。
5、某饮料厂生产一种半径为5cm的易拉罐,包装时每8瓶装一箱。现有两
种装箱方案(下图是箱底平面示意图):
图1 图2
试判断哪种装箱方案的箱底面积较小?
三.典型例题
例1.若矩形ABCD的邻边不等,分别以直线AB、BC为轴旋转一周得两个圆柱,观察这两个圆柱的底面和侧面,则有 ( ).
(A)S底S侧都相等. (B)S底不等,S侧相等.
(C) S底相等,S侧不等.(n) S底S侧都不等.
例2.如果圆台的上底面半径为5,下底面半径为R,中截面把圆台分为上、下两个圆台,它们的侧面积的比为1:2,那么R=( )
(A)10 (B)15 (C)20 (D)25
例3.用一块圆心角为150°,面积为240лcm2的扇形硬纸片围成一个圆锥模型(相交粘贴部分忽略不计),求圆锥模型的底面半径.
例4.巳知圆锥的轴截面周长为10cm,设腰长为x,圆锥的表面积为S,
(1) 求S关于X的函数表达式和自变量X的取值范围;
(2)画出这个函数图象,确定S的取值范围.
例5.如图,已知直角梯形ABCD,BC∥AD,∠B=90°,AB=5 cm ,BC=16cm,AD=4cm。(1)求以AB所在直线为轴旋转一周所得几何体的表面积;
(2)求以直线BC为轴旋转一周所得几何体的表面积.
1圆的有关概念:
掌握弦和直径之间的关系,什么是等弧,
2.垂径定理概念与规律:
圆是轴对称图形,任何经过圆形的直线都是它的对称轴。
垂直于弦的直径平分弦,并且平分弦所对的两条弧。
在圆中,解有关弦的问题时,常作“垂直于弦”的直径或半径,但往往只作出圆心到弦的垂线段作为辅助线。
例1 两个O以为圆心的同心圆,大圆弦AB和小圆相交于CD两点,AB=8厘米、CD=3厘米,大圆的半径为5厘米,求小圆的半径。
例2 已知OA、OB为⊙O的半径,OA⊥OB,弦AD经过OB的中点C,⊙O的半径为4厘米,求AD的长。
例3 如图所示,在直角三角形ABC中,∠C=90°CB=12,CA=5,以C为圆心、CA为半径作圆交AB与点D,求BD的长。
弧、弦、圆心角
如图,AB、CD是⊙O的两条弦:
(1)如果AB=CD,那么 , 。
(2)如果弧AB=CD,那么 , 。
(3)如果∠AOB=∠COD,那么 , 。
(4)如果AB=CD,OE⊥AB于E,OF⊥CD于F,OE于OF相等吗?为什么?
与有关的位置关系
点和圆的位置关系的概念与规律
1. 如果⊙O的半径为r,点到圆心O的距离为d,那么,
(1) 点P在⊙O外
(2) 点P在⊙O上
(3) 点P在⊙O内
例题 1
如图所示,⊙O的半径R=10,圆心O到直线距离OD=6,在直线OD上有A、B、C三点,BD=8,AD=6,CD=9,判别ABC三点对于圆的位置关系。
例题 2 ⊿ABC中,∠C=90°∠B=60°AC=3以C为圆心,R为半径作圆C,如果点B再圆内,而点A在圆外,那么R的范围。
例3 一点到圆上点的最大距离为9,最短距离为1,求圆的半径。
例4 如图已知矩形ABCD的边AB=3㎝、AC=4㎝
⑴以点A为圆心,4cm为半径作⊙A,则点B、C、D与⊙A的位置关系
⑵若以A点为圆心作⊙A,使B、C、D三点中至少有一点在圆内 ,
且至少有一点在圆外,则⊙A的半径r的取值范围是什么?
圆周角
概念与规律:
圆周角的两个特征:1角的顶点在圆周上。2角的两边和圆相交。
同弧和等弧所对的圆周角相等;在同圆和等圆中,相等的圆周角所对的弧相等。
半圆或直径所对的圆周角是直角,反之90度的圆周角所对的弦是直径,弧是半圆。
例:如图所示,在圆中AB为直径,半径OC⊥AB,D为弧BC上的一点,在AD上取AE=BD。判断三角形CDE的形状。
直线和圆的位置关系
概念与规律
1. 直线与圆的位置关系有三种情况:
(1) 相离----直线与圆没有公共点,此时直线到圆心的距离大于半径。
(2) 相切-----直线与圆只有一个公共点,此时直线到圆心的距离等于半径。
(3) 相交-----直线与圆有两个公共点,此时直线到圆心的距离小于半径。
例1已知⊙A的直径为6,A点坐标是(-3,-4),则⊙A与x轴的位置关系如何?与y轴的位置关系如何?
例2 如图所示,已知O为∠BAC平分线上一点,OD⊥AB,D为垂足,以O为圆心,以OD为半径作⊙O。求证⊙O和AC相切。
切线的判定:
概念与规律 1“经过半径的外端,并且垂直与半径的直线是圆的切线”。这是切线的判定定理,它把“到圆心的距离等于半径的直线是圆的切线”的定理具体化。
2要证明一直线与圆相切,必须满足两个条件:(1)过半径的外端;(2)垂直于这条半径。因此在解决相关问题时,若已知要证的直线经过圆上点,则需要把这点与圆心相连,证这直线与这半径垂直;否则需先向这直线作垂线,再证这垂线段是圆的半径。
例1 如图所示,已知AB为⊙O的直径,BC为弦,C为弧AD的中点,过C作BD的垂线交BD的延长线于E。求证:CE于⊙O相切。
例2如图所示,已知梯形ABCD中,AD∥BC,AB=DC,以DC为直径作半圆交BC于E点,EF⊥AB于F点。求证:EF于此半圆相切。
切线的性质
圆的切线垂直经过切点的半径。因此在解关于切线的问题中,通常把过切点的半径连接起来,得到90度的角。
例1如图所示已知在⊿ABC中,AB为⊙O的直径,⊙O交AB于D 点,过D点作圆的切线交BC于E点,且BE=DE。求证;BC于⊙O相切。
例2如图所示,已知AB切⊙O于E点,CD切⊙O于F点,AB∥CD,OA⊥OC,求证AC与⊙O相切。
例3 如图所示,半径为2的⊙P的圆心在直线y=2x-1上运动。
(1) 当⊙P与y轴相切时,写出P点坐标。
(2) 当⊙P与x 轴相切时,写出P点坐标。
(3) ⊙P是否能同时与x轴、y轴相切,若能,写出P点坐标,若不能请说明理由。
例4如图所示,点在⊙O直径AB 延长线上的一点,CD切⊙O于D,且DC=DA=4,CE⊥AD,交AD的延长线于E。求DE的长。
三角形的内切圆、切线长定理;
内心的性质:内心到各边的距离相等,内心与各顶点的连线构成角平分线。
三角形的内心与一边两个端点连线的夹角等于90度与第三个内角一半的和。
切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,该点与圆心的连线平分两条切线的夹角。
例1 如图,已知直角三角形ABC,∠ACB=90°I为它的内心,∠BIC=105°,AC=,求各边长及内切圆的半径。
例2 已知直角梯形ABCD中,AD∥BC,∠B=90°以AB为直径作⊙O切CD于E点。求证:OD⊥OC;若AD=9,BC=16,求梯形的周长和面积。
圆和圆的位置关系
两圆的位置关系是由半径和、差与圆心距的大小关系判定的:
d > r+R
d = r+R
R-r<d < r+R
d = R-r
d < R-r
1、⊙O1、⊙O2的半径分别为40mm和25mm,两圆相交于A、B两点。若AB=48mm,则O1O2= mm。
2、已知⊙O1与⊙O2相切,它们的半径分别为3和6,则圆心距O1O2的长为 。
3、现有半径分别为5mm和4mm的两种钢球各2个,技术员小张用它们来测量一些口小内大的机器零件的内孔直径。
(1)如图示(此图为截面示意图),小张用上述两种钢球各一个进行测量时,测得钢球顶点与孔口平面的距离分别为11mm、10mm,则此零件的内孔直径是多少?
4、在平面直角坐标系中,⊙O1与⊙O2外切,它们的半径分别为6和4。若
圆心O1的坐标为(8,0),圆心O2在坐标轴上,则点O2的坐标为 。
5、某饮料厂生产一种半径为5cm的易拉罐,包装时每8瓶装一箱。现有两
种装箱方案(下图是箱底平面示意图):
图1 图2
试判断哪种装箱方案的箱底面积较小?
三.典型例题
例1.若矩形ABCD的邻边不等,分别以直线AB、BC为轴旋转一周得两个圆柱,观察这两个圆柱的底面和侧面,则有 ( ).
(A)S底S侧都相等. (B)S底不等,S侧相等.
(C) S底相等,S侧不等.(n) S底S侧都不等.
例2.如果圆台的上底面半径为5,下底面半径为R,中截面把圆台分为上、下两个圆台,它们的侧面积的比为1:2,那么R=( )
(A)10 (B)15 (C)20 (D)25
例3.用一块圆心角为150°,面积为240лcm2的扇形硬纸片围成一个圆锥模型(相交粘贴部分忽略不计),求圆锥模型的底面半径.
例4.巳知圆锥的轴截面周长为10cm,设腰长为x,圆锥的表面积为S,
(1) 求S关于X的函数表达式和自变量X的取值范围;
(2)画出这个函数图象,确定S的取值范围.
例5.如图,已知直角梯形ABCD,BC∥AD,∠B=90°,AB=5 cm ,BC=16cm,AD=4cm。(1)求以AB所在直线为轴旋转一周所得几何体的表面积;
(2)求以直线BC为轴旋转一周所得几何体的表面积.
同课章节目录
