沪科版九年级上册二次函数应用第(1)讲销售利润问题
文档属性
| 名称 | 沪科版九年级上册二次函数应用第(1)讲销售利润问题 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-08 20:36:23 | ||
图片预览






文档简介
(共16张PPT)
二次函数应用
第(1)讲销售利润问题
沪科版九年级
学无止境
模型汇总
1、销售利润问题
动点轨迹为直线型
【数学模型】
(1)利润=售价-成本
打几折是指按定价的百分之几十出售,也就是商品的定价×打折率
(2)×100%=×100%
推导公式:①售价-成本×(1÷利润率)
②成本=
(3)总销售利润=单件利润×销售量=总销售额-总成本(不变)=(已售销售量×销售单价-固定成本)
【分析】
①分析总销售利润取最值情况时,一定要参考自变量的取值范围;
②对于多解情况,先讨论再取舍,题干中常有“若为了更多的让利消费者,则选择销售单价较低的解”
③销售量和销售单价变化符合市场逻辑,此消彼长,薄利多销的原则。
④在设销售利润的函数表达式时,有两种情况:一是直接设元(销售单价),二是间接设元(在原有销售单价基础上,增长的价格);可根据实际情况合理选用最有解法,方法不唯一。
1-1、销售利润问题-与一次函数结合
例1.(2022九上衢江月考)某超市销售一批成本为20元/千克的绿色健康食品,深受游客青睐.经市场调查发现,该食品每天的销售量y(千克)与销售单价x(元/千克)之间满足一次函数关系,其图像如图所示.
(1)求该食品每天的销售量y(干克)与销售单价x(元/千克)之间的函数关系式;
(2)若超市按售价不低于成本价,且不高于40元销售,则销售单价定为多少,才能使销售该食品每天获得的利润W(元)最大 最大利润是多少
(3)若超市要使每天销售该食品获得的利润不低于2400元,则每天的销售量最少应为__________千克.
【答案】(1)y=-2x+180
(2)
∵函数表达式对称轴为
∵-2<0,抛物线开口向下
∴当x<55时,
∴当x=40时,有最大值,最大值为2000.
∴当销售单价为40元是,销售最大利润(元),最大值为2000.
60
令=2400,根据函数的性质得;再找到对应的销售量y的值,根据实际情况取舍
1、销售利润问题-与一次函数结合
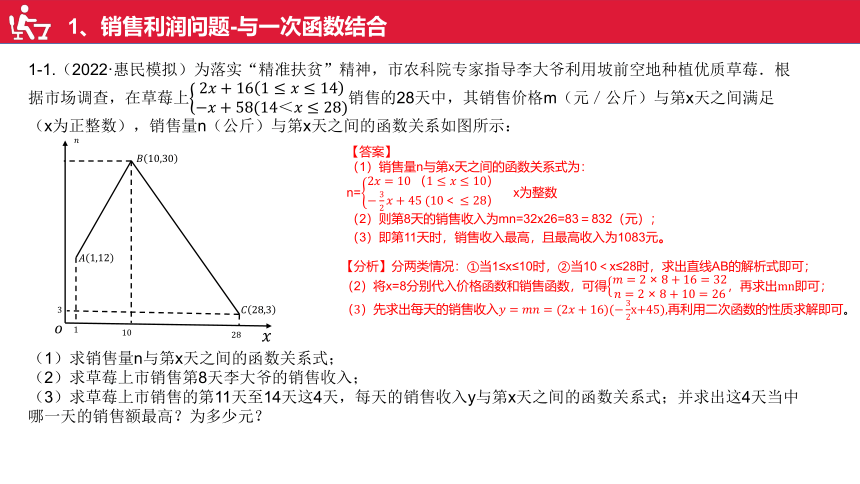
1-1.(2022·惠民模拟)为落实“精准扶贫”精神,市农科院专家指导李大爷利用坡前空地种植优质草莓.根据市场调查,在草莓上销售的28天中,其销售价格m(元/公斤)与第x天之间满足
(x为正整数),销售量n(公斤)与第x天之间的函数关系如图所示:
(1)求销售量n与第x天之间的函数关系式;
(2)求草莓上市销售第8天李大爷的销售收入;
(3)求草莓上市销售的第11天至14天这4天,每天的销售收入y与第x天之间的函数关系式;并求出这4天当中哪一天的销售额最高?为多少元?
【答案】
(1)销售量n与第x天之间的函数关系式为:
n= x为整数
(2)则第8天的销售收入为mn=32x26=83=832(元);
(3)即第11天时,销售收入最高,且最高收入为1083元。
【分析】分两类情况:①当1≤x≤10时,②当10<x≤28时,求出直线AB的解析式即可;
(2)将x=8分别代入价格函数和销售函数,可得,再求出mn即可;
(3)先求出每天的销售收入x+45),再利用二次函数的性质求解即可。
1、销售利润问题-与一次函数结合
1-2.(2022·秀洲模拟)某公司成功开发出一种产品,正式投产后,生产成本为5元/件.公司按订单生产该产品(销售量=产量),年销售量y(万件)与售价x(元/件)之间满足如图1所示的函数关系,公司规定产品售价不超过15元/件,受产能限制,年销售量不超过30万件,为了提高该产品竞争力,投入研发费用P元(P万元计入成本),P与x之间的函数关系式如图2所示,当10≤x≤15时可看成抛物线
(1)求与x之间的函数关系式。
(2)求这种产品年利润W(万元)与售价x(元件)满足的函数关系式.
(3)当售价x为多少元时,年利润W最大,并求出这个最大值.
【答案】(1)y=-2x+4
(2)①当5≤x≤10时,
②当10≤x≤15时,
(3)当x=12时,的最大值为49万元。
1-3.(2022—隆阳模拟)在乡村振兴活动中,某电商正在热销一种当地特色商品,其成本为50元/件,在销售过程中发现随着售价增加,销售量在减少,商家决定当售价为80元/件时,改变销售策略,此时售价每增加1元需支付由此产生的额外费用400元,该商品销售量y(件)与售价x(元/件)满足如图所示的函数关系(其中50(1)直接写出y与x的函数关系式;
(2)当售价为多少时,商家所获利润最大,最大利润是多少?
1、销售利润问题-与一次函数结合
【答案】(1)
(2)当售价为75元时,商家所获利润最大,最大利润为6250元。
1-2、销售利润问题-图表信息
例2.(2022长兴模拟)某大学生利用暑假40天社会实践参与了某公司旗下一家加盟店经营,了解到一种成本为20元/件的新型商品在第x天销售的相关信息如下表所示:
(1)请计算第几天该商品的销售单价为35元/件;
(2)这40天中该加盟店第几天获得的利润最大?最大利润是多少?
(3)在实际销售的前20天中,公司为鼓励加盟店接收大学生参加实践活动决定每销售一件商品就发给该加盟店m(m≥2)元奖励.通过该加盟店的销售记录发现,前10天中,每天获得奖励后的利润随时间x(天)的增大而增大,求m的取值范围.
【答案】
(1)当第5天和第35天该商品的销售单价为35元/件
(2)第21天时所获利润最大,最大利润为725元;
(3)2≤m≤5
【分析】(1)分情况讨论,当1≤x≤20时和当21≤x≤40时的函数值为35,然后求得对应的x的值即可;
(2)分为当1≤x≤20时和当21≤x≤40时两种情况,列出与天数的函数关系式,然后利用二次函数和反比例函数的性质求解即可;
(3)先求得抛物线的对称轴,讨论增减性,然后根据前10天的利润随x的增大而增大,再列出关于m的不等式求解即可;
2-1.(2022九上·永嘉月考)某食品公司通过网络平台直播,对其代理的某品牌瓜子进行促销,该公司每天拿出2000元现金,作为红包发给购买者.已知该瓜子的成本价格为7元/kg,每日销售y(kg)与销售单价x(元/kg)满足关系式:y=kx+b,,部分数据如表:
销售单价x(元/kg) 8 9 ··· 20
每日销售量(kg) 3400 3200 ··· 1000
经销售发现,销售单价不低于成本价格且不高于20元/kg.设该食品公司销售这种瓜子的日获利为w(元)
(1)y与x的函数关系式是_____________,x的范围是_______________;
(2)当销售单价定为多少时,销售这种瓜子日获利最大?最大利润为多少元?
(3)网络平台将向食品公司收取a元/kg(a<3)的相关费用,若此时日获利的最大值为12112元,直接写出a的值.
1-2、销售利润问题-图表信息
y=-200x+5000
7≤x≤20
(2)
∵a=-200<0,函数图象开口向下,有最大值
函数图象的对称轴为x=16,∵6≤x≤20,当x=16时,函数有最大值,为14200,
所以销售单价定位16元时,获利最大,为14200元;
(3)收取α元后,利润为 ∴抛物线开口向下,有最大值,
又函数图像的对称轴为∵a<4,
当时,获利最大值为42100元,将代入得,
解得a=1.2或a=37.4(舍)∴.a=1.2
2-2(2022·馆陶模拟)某公司把一种原料加工成产品进行销售,已知某月共加工原料x吨,恰好能生产相同吨数的产品并能完全销售.每吨原料的加工成本Q(万元)与x(吨)有如下关系:
(其中a、b均为常数),且在整个过程中,经过统计得到如下数据:
(1)求a、b的值;
(2)若这个月的加工总成本为2052万元,求x的值;
(3)若生产的产品每吨售价60万元,求该月可获得的最大利润是多少万元?
1-2、销售利润问题-图表信息
【答案】(1)
(2)
(3)当生产135吨时,所获最大利润是3375万元
2-3(2022·东营模拟)某文具店经营某种品牌的文具盒,购进时的单价是30元,根据统计调查:在一段时间内,销售单价是40元时,文具盒销售量是600个,而销售单价每涨2元,就会少售出20个文具盒.
(1)不妨设该种品牌文具盒的销售单价为x元(x>40),请你分别用x的代数式来表示销售量y个和销售该品牌文具盒获得利润元,并把结果填写在表格中:
(2)在(1)问条件下,若该文具店获得了6000元销售利润,求该文具盒销售单价x应定为多少元?
(3)在(1)问条件下,若厂家规定该品牌文具盒销售单价不低于44元,且文具店要完成不少于380个的销售目标,求该文具店销售该品牌文具盒获得的最大利润是多少元?
1-2、销售利润问题-图表信息
100-10x
-10x +1300x-30000
【答案】(2)若该文具店获得600元销售利润,则销售单价应定为90元.
(3)该文具店销售该品牌文具盒获取的最大利润是12160元.
1-3、销售利润问题-方案决策
例3.(2022九上东阳月考)某商场要经营一种新上市的文具,进价为20元件,试营销阶段发现:当销售单价25元/件时,每天的销售量是250件,销售单价每上涨1元,每天的销售量就减少10件.
(1)写出商场销售这种文具,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;
(3)商场的营销部结合上述情况,提出了A、B两种营销方案:
方案A:该文具的销售单价高于进价且不超过30元;
方案B:每件文具的利润不低于25元且不高于29元.请比较哪种方案的最大利润更高,并说明理由.
解:
(1)由题意得,销售量=250-10(x-25)=-10x+500 ,则w= (x-20) (-10x+500 ) =-10x +700x-10000.
(2) 解:w=-10x +700x-10000=-10(x-35) +2250
∵10<0
∴函数图象开口向下,w有最大值,
当x=35 时,=2250.当单价为35元时,该文具每天的利润最大.
(3)解:方案A利润高,理由如下:方案A中:20∴x=30时,w有最大值, 此时=2000; 方案B中:故x的取值范围为:45≤x≤49
∵函数w=-10(x-35) +2250,对称轴为直线x=35
∴ x=45时,w有最大值, 此时=1250,
∴ 方案A利润更高.
1-3、销售利润问题-方案决策
3-1(2022九上舟山月考)我市某苗木种植基地尝试用单价随天数而变化的销售模式销售某种果苗,利用30天时间销售一种成本0元/株的果苗,售后经过统计得到此果苗,单日销售量n(株)与第x天(x为整数)满足关系式:n=-x+50,销售单价m(元/株)与x之间的函数关系为
(1)计算第几天该果苗单价为25元/株?
(2)求该基地销售这种果苗30天里单日所获利润y(元)关于x(天)的函数关系式;
(3)“吃水不忘挖井人”,为回馈本地居民,基地负责人决定将这30天中,其中获利最多的那天的利润全部捐出,进行“精准扶贫”试问:基地负责人这次为“精准扶贫”捐赠多少钱?
答:第10天或第28天该果苗单价为25元/株;
(2)求函数关系式为:
(3) 答:基地负责人向“精准扶贫”捐了612.5元.
1-3、销售利润问题-方案决策
3-2(2022九上舟山月考)某水果批发店推出一款拼盘水果(盒装),经市场调查表明,若售价为45元/盒,日销售量为110盒,若售价每提高1元/盒,日销售量将减少2盒.设每盒售价为x元(x≥45,且为整数).
(1)若某日销售量为90盒,求该日每盒的售价.
(2)设每日销售额为W元,求W关于x的函数表达式,并求W的最大值.
(3)该水果店每天支付店租m元后(m为正整数),发现最大日收入(日收入=销售额—店租)不超过4880元,并有且只有5种不同的单价使日收入不少于4870元,请写出所有符合条件的m的值.
解:,该日每盒的售价是55元.
解:
(2)W=x×[110-2(x-45)]=-2x +200x=-2(x-50) +5000
当x=50时,W取到最大值是5000.
解:支付店租m元后的收入是W-m=-2(x-50) +5000-m 最大日收入不超过4880元,
5000-m≤4880
解得:m≥12
只有5种不同的单价使日收入不少于4870元,-2(52-50) +5000-m≥4870
解得m≤12 .故符合条件的m的值是120或121或122.
1-3、销售利润问题-方案决策
3-3(2022·龙湾模拟)某商场出售A商品,该商品按进价提高50%后出售,售出10件可获利100元.
(1)求A商品每件的进价和售价分别是多少元?
(2)已知A商品每星期卖出200件,为提高A商品的利润,商场市场部进行了调查,获得以下反馈信息:
①结合上述两条信息,A商品售价为多少元时,利润最大?
②某顾客带320元到商场购买A、B两种商品至少各1件(A商品为第①小题中利润最大时的售价),B商品售价为25元/个,现要求A商品的数量不少于B商品的数量.在不超额的前提下,如何购买这两种商品,使在总数量最多的情况下,总费用最少.
信息一:每涨价1元,每星期会少卖出10件. 信息二:每降价1元,每星期可多卖出25件.
(1)答:A商品每件的进价和售价分别是20,30元;
解:①设售价为x元,获得利润为w元当商品涨价时,则x≥30,此时销售量为200-10x(x-30)=500-10x
件, w=(x-20)(500-10x)=-10x +700x-10000=-10(x-35) +2250 则当x=35时,w最大,为2250,当商品降价时,则x<30
此时销售量为200+25x(30-x)=950-25x件
w=(x-20)(950-25x)=-25x +1450x-19000=-25(x-29) +2025
当x=29时,w最大,为2025,2025<2250
x=35时,w最大,为2250,
答:A商品售价为35元时,利润最大;
②设购买A商品数量为m个,B商品数量为n个,
由题意可得:且m,n为正整数
当m=1 ,n=1时,35m+25n=60 ,符合题意;
当m=2,n=2时, 35m+25n=120 ,符合题意;
当m=3,n=3时, 35m+25n=180 ,符合题意;
当m=4,n=4时, 35m+25n=240 ,符合题意;
当m=5,n=5时, 35m+25n=300 ,符合题意;
当m=6,n=5时, 35m+25n=335>320 ,不符合题意;
综上,在总数量最多的情况下,购买A,B商品的数量都为5个时,
总费用最少,
1-3、销售利润问题-方案决策
3-4(2022·雁塔模拟)某厂商投产一种新型科技产品,每件制造成本为18元,试销过程中发现,每月销售量y(万件)与销售单价x(元)之间的关系可以近似地看作一次函数y=-2x+100
(1)写出每月的利润L(万元)与销售单价x(元)之间的函数关系式;
(2)当销售单价为多少元时,厂商每月能获得312万元的利润?当销售单价为多少元时,厂商每月能获得最大利润?最大利润是多少?
(3)根据相关部门规定,这种科技产品的销售单价不能高于32元,如果厂商要获得每月不低于312万元的利润,那么制造出这种产品每月的最低制造成本需要多少万元?
(1)解:L=(x-18)y=(x-18)(-2x+100)=-2x +136x-1800 ,
∴L与x之间的函数解析式为L=-2x +136x-1800 ;
解:由题意得:
L=312 ,则有
312=-2x +136x-1800 解这个方程得
所以,销售单价定为24元或44元,将
L=-2x +136x-1800配方,得
L=-2(x-34) +512
∵-2<0
∴当销售单价为34元时,每月能获得最大利润,最大利润是512万元;
结合(2)及函数
L=-2x +136x-1800的图象(如图所示)可知,
当24≤x≤44时L≥312 又由限价32元,得
24≤x≤32
根据一次函数的性质,得y=-2x+100中y随x的增大而减小,∴当x=32时,每月制造成本最低.,
因此,所求每月最低制造成本为648万元.
二次函数应用
第(1)讲销售利润问题
沪科版九年级
学无止境
模型汇总
1、销售利润问题
动点轨迹为直线型
【数学模型】
(1)利润=售价-成本
打几折是指按定价的百分之几十出售,也就是商品的定价×打折率
(2)×100%=×100%
推导公式:①售价-成本×(1÷利润率)
②成本=
(3)总销售利润=单件利润×销售量=总销售额-总成本(不变)=(已售销售量×销售单价-固定成本)
【分析】
①分析总销售利润取最值情况时,一定要参考自变量的取值范围;
②对于多解情况,先讨论再取舍,题干中常有“若为了更多的让利消费者,则选择销售单价较低的解”
③销售量和销售单价变化符合市场逻辑,此消彼长,薄利多销的原则。
④在设销售利润的函数表达式时,有两种情况:一是直接设元(销售单价),二是间接设元(在原有销售单价基础上,增长的价格);可根据实际情况合理选用最有解法,方法不唯一。
1-1、销售利润问题-与一次函数结合
例1.(2022九上衢江月考)某超市销售一批成本为20元/千克的绿色健康食品,深受游客青睐.经市场调查发现,该食品每天的销售量y(千克)与销售单价x(元/千克)之间满足一次函数关系,其图像如图所示.
(1)求该食品每天的销售量y(干克)与销售单价x(元/千克)之间的函数关系式;
(2)若超市按售价不低于成本价,且不高于40元销售,则销售单价定为多少,才能使销售该食品每天获得的利润W(元)最大 最大利润是多少
(3)若超市要使每天销售该食品获得的利润不低于2400元,则每天的销售量最少应为__________千克.
【答案】(1)y=-2x+180
(2)
∵函数表达式对称轴为
∵-2<0,抛物线开口向下
∴当x<55时,
∴当x=40时,有最大值,最大值为2000.
∴当销售单价为40元是,销售最大利润(元),最大值为2000.
60
令=2400,根据函数的性质得;再找到对应的销售量y的值,根据实际情况取舍
1、销售利润问题-与一次函数结合
1-1.(2022·惠民模拟)为落实“精准扶贫”精神,市农科院专家指导李大爷利用坡前空地种植优质草莓.根据市场调查,在草莓上销售的28天中,其销售价格m(元/公斤)与第x天之间满足
(x为正整数),销售量n(公斤)与第x天之间的函数关系如图所示:
(1)求销售量n与第x天之间的函数关系式;
(2)求草莓上市销售第8天李大爷的销售收入;
(3)求草莓上市销售的第11天至14天这4天,每天的销售收入y与第x天之间的函数关系式;并求出这4天当中哪一天的销售额最高?为多少元?
【答案】
(1)销售量n与第x天之间的函数关系式为:
n= x为整数
(2)则第8天的销售收入为mn=32x26=83=832(元);
(3)即第11天时,销售收入最高,且最高收入为1083元。
【分析】分两类情况:①当1≤x≤10时,②当10<x≤28时,求出直线AB的解析式即可;
(2)将x=8分别代入价格函数和销售函数,可得,再求出mn即可;
(3)先求出每天的销售收入x+45),再利用二次函数的性质求解即可。
1、销售利润问题-与一次函数结合
1-2.(2022·秀洲模拟)某公司成功开发出一种产品,正式投产后,生产成本为5元/件.公司按订单生产该产品(销售量=产量),年销售量y(万件)与售价x(元/件)之间满足如图1所示的函数关系,公司规定产品售价不超过15元/件,受产能限制,年销售量不超过30万件,为了提高该产品竞争力,投入研发费用P元(P万元计入成本),P与x之间的函数关系式如图2所示,当10≤x≤15时可看成抛物线
(1)求与x之间的函数关系式。
(2)求这种产品年利润W(万元)与售价x(元件)满足的函数关系式.
(3)当售价x为多少元时,年利润W最大,并求出这个最大值.
【答案】(1)y=-2x+4
(2)①当5≤x≤10时,
②当10≤x≤15时,
(3)当x=12时,的最大值为49万元。
1-3.(2022—隆阳模拟)在乡村振兴活动中,某电商正在热销一种当地特色商品,其成本为50元/件,在销售过程中发现随着售价增加,销售量在减少,商家决定当售价为80元/件时,改变销售策略,此时售价每增加1元需支付由此产生的额外费用400元,该商品销售量y(件)与售价x(元/件)满足如图所示的函数关系(其中50
(2)当售价为多少时,商家所获利润最大,最大利润是多少?
1、销售利润问题-与一次函数结合
【答案】(1)
(2)当售价为75元时,商家所获利润最大,最大利润为6250元。
1-2、销售利润问题-图表信息
例2.(2022长兴模拟)某大学生利用暑假40天社会实践参与了某公司旗下一家加盟店经营,了解到一种成本为20元/件的新型商品在第x天销售的相关信息如下表所示:
(1)请计算第几天该商品的销售单价为35元/件;
(2)这40天中该加盟店第几天获得的利润最大?最大利润是多少?
(3)在实际销售的前20天中,公司为鼓励加盟店接收大学生参加实践活动决定每销售一件商品就发给该加盟店m(m≥2)元奖励.通过该加盟店的销售记录发现,前10天中,每天获得奖励后的利润随时间x(天)的增大而增大,求m的取值范围.
【答案】
(1)当第5天和第35天该商品的销售单价为35元/件
(2)第21天时所获利润最大,最大利润为725元;
(3)2≤m≤5
【分析】(1)分情况讨论,当1≤x≤20时和当21≤x≤40时的函数值为35,然后求得对应的x的值即可;
(2)分为当1≤x≤20时和当21≤x≤40时两种情况,列出与天数的函数关系式,然后利用二次函数和反比例函数的性质求解即可;
(3)先求得抛物线的对称轴,讨论增减性,然后根据前10天的利润随x的增大而增大,再列出关于m的不等式求解即可;
2-1.(2022九上·永嘉月考)某食品公司通过网络平台直播,对其代理的某品牌瓜子进行促销,该公司每天拿出2000元现金,作为红包发给购买者.已知该瓜子的成本价格为7元/kg,每日销售y(kg)与销售单价x(元/kg)满足关系式:y=kx+b,,部分数据如表:
销售单价x(元/kg) 8 9 ··· 20
每日销售量(kg) 3400 3200 ··· 1000
经销售发现,销售单价不低于成本价格且不高于20元/kg.设该食品公司销售这种瓜子的日获利为w(元)
(1)y与x的函数关系式是_____________,x的范围是_______________;
(2)当销售单价定为多少时,销售这种瓜子日获利最大?最大利润为多少元?
(3)网络平台将向食品公司收取a元/kg(a<3)的相关费用,若此时日获利的最大值为12112元,直接写出a的值.
1-2、销售利润问题-图表信息
y=-200x+5000
7≤x≤20
(2)
∵a=-200<0,函数图象开口向下,有最大值
函数图象的对称轴为x=16,∵6≤x≤20,当x=16时,函数有最大值,为14200,
所以销售单价定位16元时,获利最大,为14200元;
(3)收取α元后,利润为 ∴抛物线开口向下,有最大值,
又函数图像的对称轴为∵a<4,
当时,获利最大值为42100元,将代入得,
解得a=1.2或a=37.4(舍)∴.a=1.2
2-2(2022·馆陶模拟)某公司把一种原料加工成产品进行销售,已知某月共加工原料x吨,恰好能生产相同吨数的产品并能完全销售.每吨原料的加工成本Q(万元)与x(吨)有如下关系:
(其中a、b均为常数),且在整个过程中,经过统计得到如下数据:
(1)求a、b的值;
(2)若这个月的加工总成本为2052万元,求x的值;
(3)若生产的产品每吨售价60万元,求该月可获得的最大利润是多少万元?
1-2、销售利润问题-图表信息
【答案】(1)
(2)
(3)当生产135吨时,所获最大利润是3375万元
2-3(2022·东营模拟)某文具店经营某种品牌的文具盒,购进时的单价是30元,根据统计调查:在一段时间内,销售单价是40元时,文具盒销售量是600个,而销售单价每涨2元,就会少售出20个文具盒.
(1)不妨设该种品牌文具盒的销售单价为x元(x>40),请你分别用x的代数式来表示销售量y个和销售该品牌文具盒获得利润元,并把结果填写在表格中:
(2)在(1)问条件下,若该文具店获得了6000元销售利润,求该文具盒销售单价x应定为多少元?
(3)在(1)问条件下,若厂家规定该品牌文具盒销售单价不低于44元,且文具店要完成不少于380个的销售目标,求该文具店销售该品牌文具盒获得的最大利润是多少元?
1-2、销售利润问题-图表信息
100-10x
-10x +1300x-30000
【答案】(2)若该文具店获得600元销售利润,则销售单价应定为90元.
(3)该文具店销售该品牌文具盒获取的最大利润是12160元.
1-3、销售利润问题-方案决策
例3.(2022九上东阳月考)某商场要经营一种新上市的文具,进价为20元件,试营销阶段发现:当销售单价25元/件时,每天的销售量是250件,销售单价每上涨1元,每天的销售量就减少10件.
(1)写出商场销售这种文具,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;
(3)商场的营销部结合上述情况,提出了A、B两种营销方案:
方案A:该文具的销售单价高于进价且不超过30元;
方案B:每件文具的利润不低于25元且不高于29元.请比较哪种方案的最大利润更高,并说明理由.
解:
(1)由题意得,销售量=250-10(x-25)=-10x+500 ,则w= (x-20) (-10x+500 ) =-10x +700x-10000.
(2) 解:w=-10x +700x-10000=-10(x-35) +2250
∵10<0
∴函数图象开口向下,w有最大值,
当x=35 时,=2250.当单价为35元时,该文具每天的利润最大.
(3)解:方案A利润高,理由如下:方案A中:20
∵函数w=-10(x-35) +2250,对称轴为直线x=35
∴ x=45时,w有最大值, 此时=1250,
∴ 方案A利润更高.
1-3、销售利润问题-方案决策
3-1(2022九上舟山月考)我市某苗木种植基地尝试用单价随天数而变化的销售模式销售某种果苗,利用30天时间销售一种成本0元/株的果苗,售后经过统计得到此果苗,单日销售量n(株)与第x天(x为整数)满足关系式:n=-x+50,销售单价m(元/株)与x之间的函数关系为
(1)计算第几天该果苗单价为25元/株?
(2)求该基地销售这种果苗30天里单日所获利润y(元)关于x(天)的函数关系式;
(3)“吃水不忘挖井人”,为回馈本地居民,基地负责人决定将这30天中,其中获利最多的那天的利润全部捐出,进行“精准扶贫”试问:基地负责人这次为“精准扶贫”捐赠多少钱?
答:第10天或第28天该果苗单价为25元/株;
(2)求函数关系式为:
(3) 答:基地负责人向“精准扶贫”捐了612.5元.
1-3、销售利润问题-方案决策
3-2(2022九上舟山月考)某水果批发店推出一款拼盘水果(盒装),经市场调查表明,若售价为45元/盒,日销售量为110盒,若售价每提高1元/盒,日销售量将减少2盒.设每盒售价为x元(x≥45,且为整数).
(1)若某日销售量为90盒,求该日每盒的售价.
(2)设每日销售额为W元,求W关于x的函数表达式,并求W的最大值.
(3)该水果店每天支付店租m元后(m为正整数),发现最大日收入(日收入=销售额—店租)不超过4880元,并有且只有5种不同的单价使日收入不少于4870元,请写出所有符合条件的m的值.
解:,该日每盒的售价是55元.
解:
(2)W=x×[110-2(x-45)]=-2x +200x=-2(x-50) +5000
当x=50时,W取到最大值是5000.
解:支付店租m元后的收入是W-m=-2(x-50) +5000-m 最大日收入不超过4880元,
5000-m≤4880
解得:m≥12
只有5种不同的单价使日收入不少于4870元,-2(52-50) +5000-m≥4870
解得m≤12 .故符合条件的m的值是120或121或122.
1-3、销售利润问题-方案决策
3-3(2022·龙湾模拟)某商场出售A商品,该商品按进价提高50%后出售,售出10件可获利100元.
(1)求A商品每件的进价和售价分别是多少元?
(2)已知A商品每星期卖出200件,为提高A商品的利润,商场市场部进行了调查,获得以下反馈信息:
①结合上述两条信息,A商品售价为多少元时,利润最大?
②某顾客带320元到商场购买A、B两种商品至少各1件(A商品为第①小题中利润最大时的售价),B商品售价为25元/个,现要求A商品的数量不少于B商品的数量.在不超额的前提下,如何购买这两种商品,使在总数量最多的情况下,总费用最少.
信息一:每涨价1元,每星期会少卖出10件. 信息二:每降价1元,每星期可多卖出25件.
(1)答:A商品每件的进价和售价分别是20,30元;
解:①设售价为x元,获得利润为w元当商品涨价时,则x≥30,此时销售量为200-10x(x-30)=500-10x
件, w=(x-20)(500-10x)=-10x +700x-10000=-10(x-35) +2250 则当x=35时,w最大,为2250,当商品降价时,则x<30
此时销售量为200+25x(30-x)=950-25x件
w=(x-20)(950-25x)=-25x +1450x-19000=-25(x-29) +2025
当x=29时,w最大,为2025,2025<2250
x=35时,w最大,为2250,
答:A商品售价为35元时,利润最大;
②设购买A商品数量为m个,B商品数量为n个,
由题意可得:且m,n为正整数
当m=1 ,n=1时,35m+25n=60 ,符合题意;
当m=2,n=2时, 35m+25n=120 ,符合题意;
当m=3,n=3时, 35m+25n=180 ,符合题意;
当m=4,n=4时, 35m+25n=240 ,符合题意;
当m=5,n=5时, 35m+25n=300 ,符合题意;
当m=6,n=5时, 35m+25n=335>320 ,不符合题意;
综上,在总数量最多的情况下,购买A,B商品的数量都为5个时,
总费用最少,
1-3、销售利润问题-方案决策
3-4(2022·雁塔模拟)某厂商投产一种新型科技产品,每件制造成本为18元,试销过程中发现,每月销售量y(万件)与销售单价x(元)之间的关系可以近似地看作一次函数y=-2x+100
(1)写出每月的利润L(万元)与销售单价x(元)之间的函数关系式;
(2)当销售单价为多少元时,厂商每月能获得312万元的利润?当销售单价为多少元时,厂商每月能获得最大利润?最大利润是多少?
(3)根据相关部门规定,这种科技产品的销售单价不能高于32元,如果厂商要获得每月不低于312万元的利润,那么制造出这种产品每月的最低制造成本需要多少万元?
(1)解:L=(x-18)y=(x-18)(-2x+100)=-2x +136x-1800 ,
∴L与x之间的函数解析式为L=-2x +136x-1800 ;
解:由题意得:
L=312 ,则有
312=-2x +136x-1800 解这个方程得
所以,销售单价定为24元或44元,将
L=-2x +136x-1800配方,得
L=-2(x-34) +512
∵-2<0
∴当销售单价为34元时,每月能获得最大利润,最大利润是512万元;
结合(2)及函数
L=-2x +136x-1800的图象(如图所示)可知,
当24≤x≤44时L≥312 又由限价32元,得
24≤x≤32
根据一次函数的性质,得y=-2x+100中y随x的增大而减小,∴当x=32时,每月制造成本最低.,
因此,所求每月最低制造成本为648万元.
