圆周角练习[上学期]
图片预览





文档简介
课件20张PPT。 1.己知:⊙o的半径为1,点P与圆心O的距离为d,且方程X2一2X +d=o有实数根,则点P在__ 2.已知⊙O的半径是5, 点O的坐标是(0, 0),点P的坐标是(4,-2).则点P与⊙O的位置关系是__3.如图△ABC的三个顶点在⊙O上,AM平分∠BAC交⊙O与点M,AD⊥Bc于D,试证明∠MA0=∠MADN 4.在圆中,弦AB与CD垂直相交于点E.
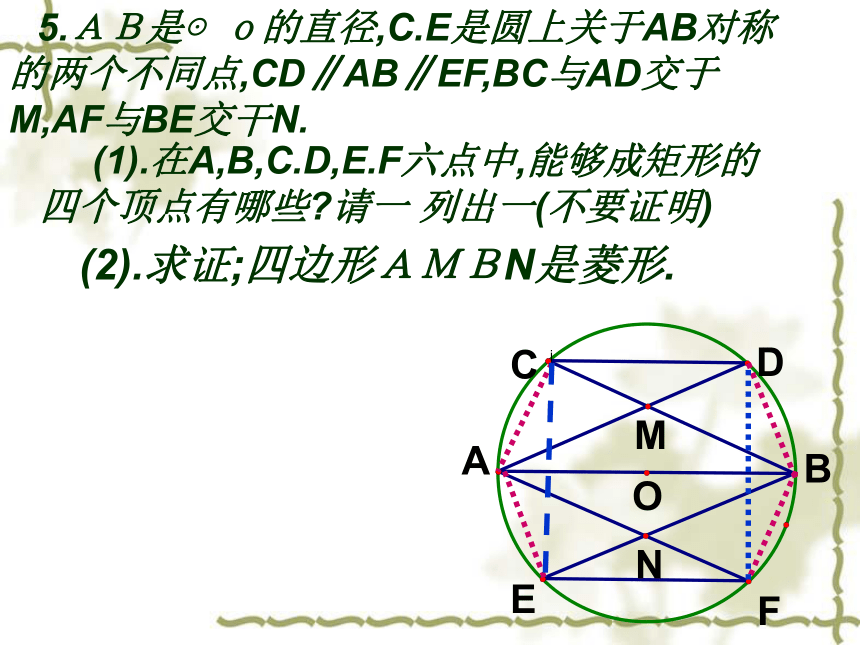
求证;∠BOC +∠ AOD=180°. 5.AB是⊙o的直径,C.E是圆上关于AB对称的两个不同点,CD∥AB∥EF,BC与AD交于M,AF与BE交干N.
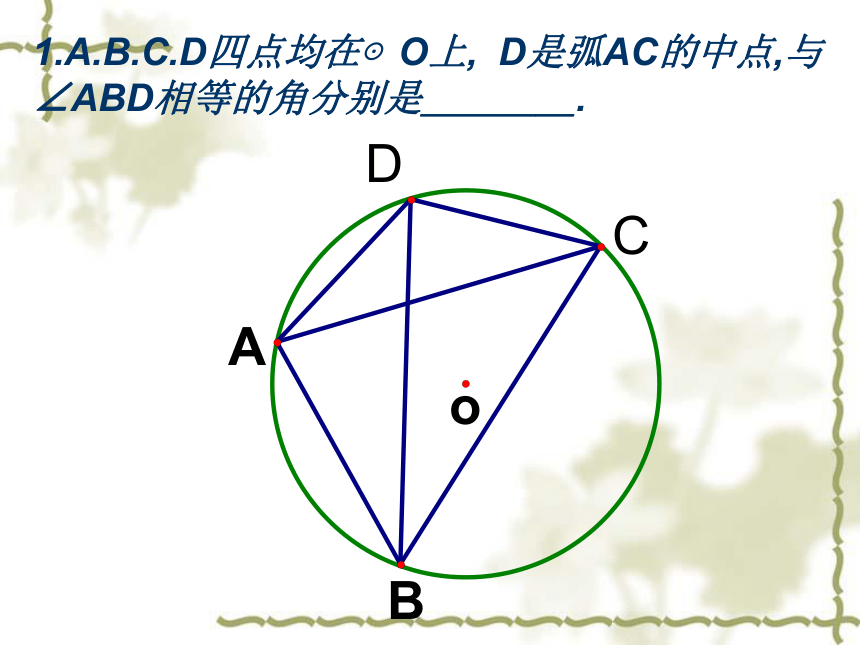
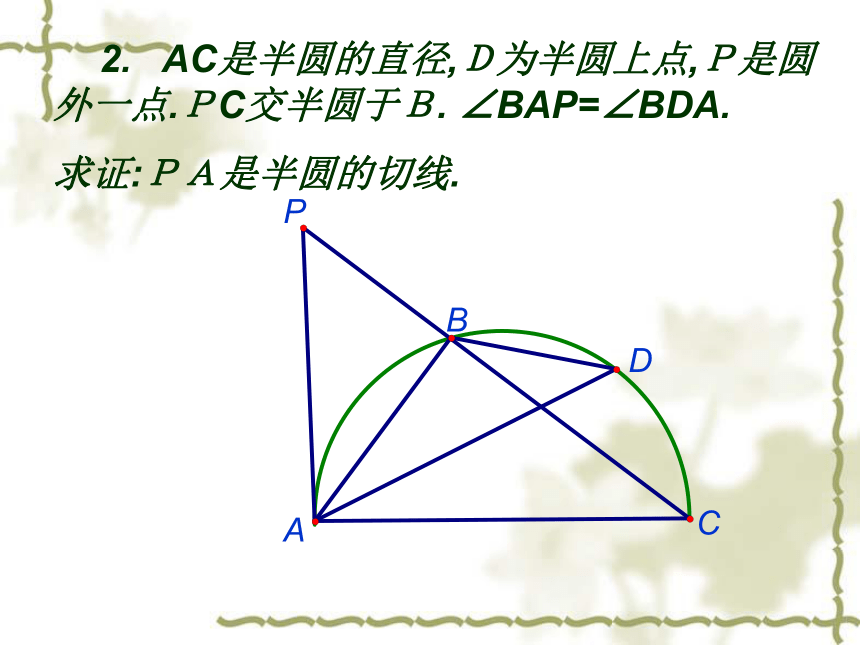
(1).在A,B,C.D,E.F六点中,能够成矩形的四个顶点有哪些?请一 列出一(不要证明) (2).求证;四边形AMBN是菱形. 3.A.B.C是⊙O上三点,点E.F分别是弧AB.弧AC的中点,连结DE分别交AB.AC于点F.G.请猜想AF与AG的关糸,说明理由.MN1.A.B.C.D四点均在⊙O上, D是弧AC的中点,与∠ABD相等的角分别是____.BACDP 2. AC是半圆的直径,D为半圆上点,P是圆外一点.PC交半圆于B. ∠BAP=∠BDA.
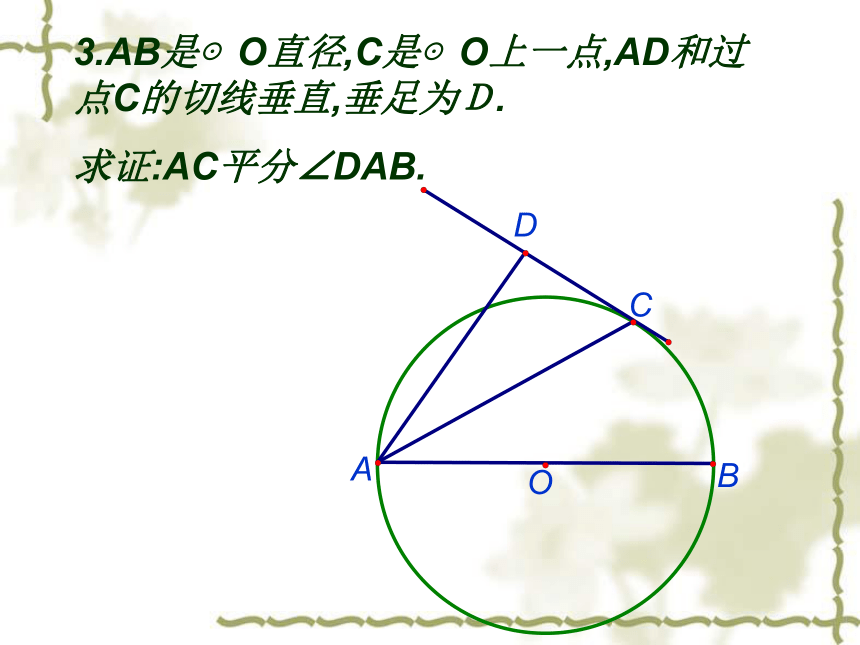
求证:PA是半圆的切线.3.AB是⊙O直径,C是⊙O上一点,AD和过点C的切线垂直,垂足为D.
求证:AC平分∠DAB.ABOCDABOCDEF 4.直角梯形ABCD中,AD∥BC,AB是⊙O的直径,DC切⊙O于F,BC交⊙O于E, 已知 : BC=8,AD=2,求梯形的面积.BD FE6.己知PA.PB是⊙O的切线,A.B是切点,弦AB的长是2√ ∠AOB=120°
求圆的半径,PA,PO的长,判定△ABP的形状.-32.-块正三角形木板沾水平线翻滚,边长是1,那么点B从开始至结束所走过的路径长度为__AABBBCC1.从图中你能想到什么? 2.从图中你能想到什么?如果弦AB=4cm,你能求得圆环的面积吗? 3.PA. PA是⊙O的切线,这个图形你能识别吗? 它可能有哪些结论? 若 OA=1, OP=2. 你能求出哪些量呢? 5.从下图你联想到了什么? 6.从下图你联想到了什么? 7.从下图你联想到了什么?
AB在什么情况下是圆的直径?
如果,AD=2, BC=8, 你能求得什么量呢? 8.你认为图中应给哪些条件?可以得到哪些结论呢?
求证;∠BOC +∠ AOD=180°. 5.AB是⊙o的直径,C.E是圆上关于AB对称的两个不同点,CD∥AB∥EF,BC与AD交于M,AF与BE交干N.
(1).在A,B,C.D,E.F六点中,能够成矩形的四个顶点有哪些?请一 列出一(不要证明) (2).求证;四边形AMBN是菱形. 3.A.B.C是⊙O上三点,点E.F分别是弧AB.弧AC的中点,连结DE分别交AB.AC于点F.G.请猜想AF与AG的关糸,说明理由.MN1.A.B.C.D四点均在⊙O上, D是弧AC的中点,与∠ABD相等的角分别是____.BACDP 2. AC是半圆的直径,D为半圆上点,P是圆外一点.PC交半圆于B. ∠BAP=∠BDA.
求证:PA是半圆的切线.3.AB是⊙O直径,C是⊙O上一点,AD和过点C的切线垂直,垂足为D.
求证:AC平分∠DAB.ABOCDABOCDEF 4.直角梯形ABCD中,AD∥BC,AB是⊙O的直径,DC切⊙O于F,BC交⊙O于E, 已知 : BC=8,AD=2,求梯形的面积.BD FE6.己知PA.PB是⊙O的切线,A.B是切点,弦AB的长是2√ ∠AOB=120°
求圆的半径,PA,PO的长,判定△ABP的形状.-32.-块正三角形木板沾水平线翻滚,边长是1,那么点B从开始至结束所走过的路径长度为__AABBBCC1.从图中你能想到什么? 2.从图中你能想到什么?如果弦AB=4cm,你能求得圆环的面积吗? 3.PA. PA是⊙O的切线,这个图形你能识别吗? 它可能有哪些结论? 若 OA=1, OP=2. 你能求出哪些量呢? 5.从下图你联想到了什么? 6.从下图你联想到了什么? 7.从下图你联想到了什么?
AB在什么情况下是圆的直径?
如果,AD=2, BC=8, 你能求得什么量呢? 8.你认为图中应给哪些条件?可以得到哪些结论呢?
同课章节目录
