冀教版数学八年级上册 16.2 线段的垂直平分线 第一课时 课件(共17张PPT)
文档属性
| 名称 | 冀教版数学八年级上册 16.2 线段的垂直平分线 第一课时 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 184.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-07 18:41:04 | ||
图片预览





文档简介
(共17张PPT)
线段的垂直平分线
第一课时
如图所示,木条l与AB钉在一起,l垂直平分AB,P1,P2,P3,…是l上的点,分别量一量点P1,P2,P3,…到A与B的距离,你有什么发现
问题思考
1.用平面图将上述问题进行转化,已知线段AB及AB的垂直平分线l,在l上取P1,P2,P3,…,连接AP1,BP1,AP2,BP2,AP3,BP3……
2.作好图后,用直尺量出AP1,BP1,AP2,BP2,AP3,BP3……讨论发现什么样的规律.
学习新知
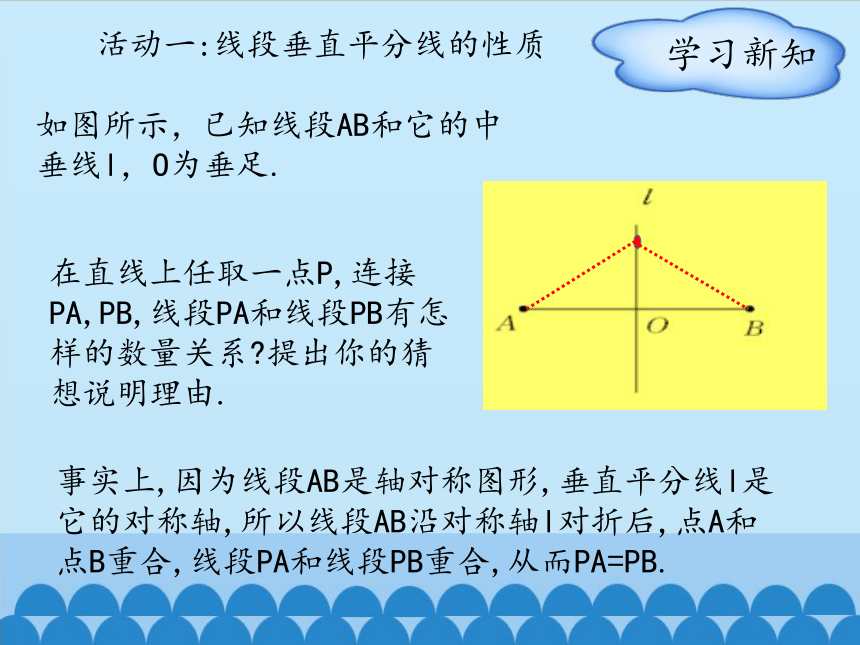
活动一:线段垂直平分线的性质
如图所示,已知线段AB和它的中垂线l,O为垂足.
在直线上任取一点P,连接PA,PB,线段PA和线段PB有怎样的数量关系 提出你的猜想说明理由.
事实上,因为线段AB是轴对称图形,垂直平分线l是它的对称轴,所以线段AB沿对称轴l对折后,点A和点B重合,线段PA和线段PB重合,从而PA=PB.
(3)这个定理向我们提供了一个证明线段相等的方法.(说明:今后我们可以直接利用这个性质得到有关线段相等,同时这也可当作等腰三角形的一种判定方法.)
[知识拓展]
(1)线段垂直平分线的性质是线段垂直平分线上所有点都具有的共同特征,即线段垂直平分线上的每一个点到线段两端的距离都相等.
(2)由性质定理的证明可知,要证明一个图形上每一个点都具有这种性质,只需要在图形上任取一点代表即可.
例题讲解
已知:如图所示,点A,B是直线外的任意两点,在直线l上,试确定一点P,使AP+BP最短.
解:如图所示,作点A关于直线l的对称点A',连接A'B,交直线l于点P,则AP+BP最短.
A'
P
【提出问题】
(1)我们知道两点之间线段最短,那么怎样把PA和PB这两条线段转化到一条线段上
(2)在直线l上任取一个异于点P的点P',怎样利用“两点之间线段最短”加以证明.
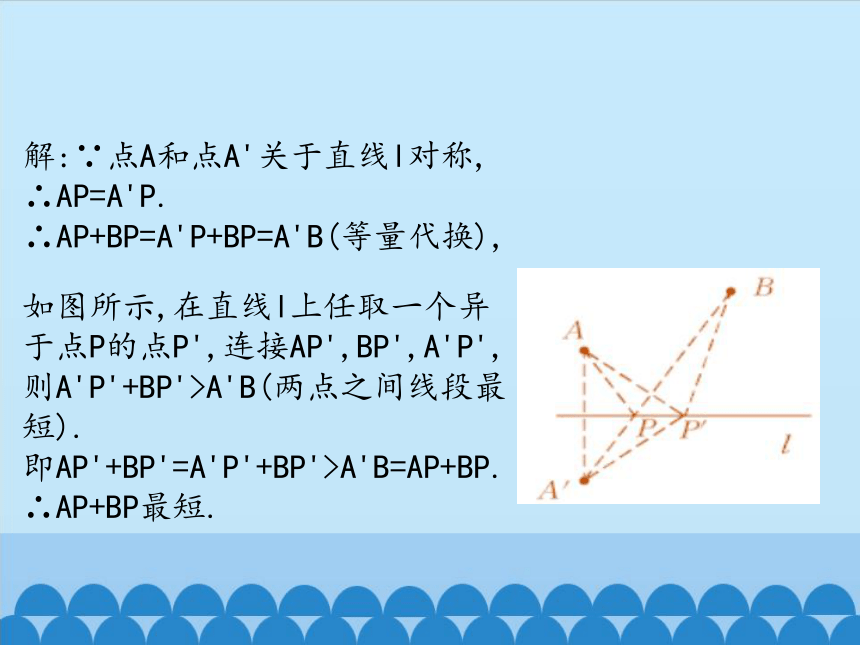
解:∵点A和点A'关于直线l对称,
∴AP=A'P.
∴AP+BP=A'P+BP=A'B(等量代换),
如图所示,在直线l上任取一个异于点P的点P',连接AP',BP',A'P',则A'P'+BP'>A'B(两点之间线段最短).
即AP'+BP'=A'P'+BP'>A'B=AP+BP.
∴AP+BP最短.
已知:如图所示,D,E分别是AB,AC的中点,CD⊥AB于点D,BE⊥AC于点E. 求证AC=AB.
证明:连接BC,因为点D,E分别是AB,AC的中点,CD⊥AB,BE⊥AC,所以CD,BE分别是AB,AC的垂直平分线,所以AC=BC,AB=CB,所以AC=AB.
(3)这个定理向我们提供了一个证明两条线段相等的方法.
课堂小结
线段垂直平分线上的点到线段两端的距离相等.
注意:(1)线段垂直平分线的性质是线段垂直平分线上所有点都具有的特征,即线段垂直平分线上的每一个点到线段两端的距离都相等.
(2)由性质定理的证明可知,要证明一个图形上每一个点都具有某种性质,只需要在图形上任取一点作代表即可,应注意理解和掌握这种由特殊到一般的思想方法.
检测反馈
1.(2015·随州中考)如图所示,ΔABC中,AB=5,AC=6,BC=4,边AB的垂直平分线交AC于点D,则ΔBDC的周长是( )
A.8 B.9 C.10 D.11
解析:∵ED是AB的垂直平分线,∴AD=BD,又ΔBDC的周长为DB+BC+CD,∴ΔBDC的周长为AD+BC+CD=AC+BC=6+4=10.故选C.
C
2.(2015·达州中考)如图所示,ΔABC中,BD平分∠ABC,BC的垂直平分线交BC于点E,交BD于点F,连接CF.若∠A=60°,∠ABD=24°,则∠ACF的度数为(提示:等腰三角形的两个底角相等) ( )
A.48° B.36° C.30 D.24°
解析:∵BD平分∠ABC,
∴∠DBC=∠ABD=24°,∵∠A=60°,∴∠ACB=180°- 60°- 24°×2=72°,∵BC的垂直平分线交BD于点F,∴BF=CF,∴ΔBFC为等腰三角形,∴∠FCB=24°,∴∠ACF=72°-24°=48°.故选A.
A
3.(2015·遂宁中考)如图所示,在ΔABC中,
AC=4cm,线段AB的垂直平分线交AC于点N,ΔBCN的周长是7cm,则BC的长为( )
A.1cm B.2cm C.3cm D.4cm
解析:∵MN是线段AB的垂直平分线,
∴AN=BN,∵ΔBCN的周长是7cm,∴BN+NC+BC=7cm,∴AN+NC+BC=7cm,
∵AN+NC=AC,∴AC+BC=7cm,
又∵AC=4cm,∴BC=7-4=3(cm).故选C.
C
4.如图所示,ΔABC中,DE是AC的垂直平分线,AE=4cm,ΔABD的周长为14cm,则ΔABC的周长为 ( )
A.18cm B.22cm
C.24cm D.26cm
解析:∵DE是AC的垂直平分线,
∴AD=CD,∴ΔABD的周长为AB+BD+AD=AB+BD+CD=AB+BC,∵AE=4cm,∴AC=2AE=2×4=8(cm),∴ΔABC的周长为AB+BC+AC=14+8=22(cm).故选B.
B
5.如图所示,四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是(提示:等腰三角形的两个底角相等)( )
A.AB=AD B.∠ABC=∠ADC
C.AB=BD D.ΔBEC≌ΔDEC
解析:∵AC垂直平分BD,
∴AB=AD,BC=CD,∴∠ABD=∠ADB,∠DBC=∠BDC,∴∠ABD+∠DBC=∠ADB+∠BDC,即∠ABC=∠ADC,EB=DE,在RtΔBCE和RtΔDCE中,
∴RtΔBCE≌RtΔDCE(HL).故选C.
C
6.如图所示,在ΔABC中,AB=AC,∠A=36°,AB的垂直平分线DE交AC于D,交AB于E,下列结论错误的是(提示:等腰三角形的两个底角相等,如果一个三角形有两个角相等,那么这个三角形是等腰三角形)( )
A.BD平分∠ABC
B.ΔBCD的周长等于AB+BC
C.AD=BD=BC
D.点D是线段AC的中点
解析:∵在ΔABC中,AB=AC,∠A=36°,
∴∠ABC=∠C= =72°,
∵AB的垂直平分线是DE,∴AD=BD,∴∠ABD=∠A=36°,∴∠DBC=∠ABC-∠ABD=72°-36°=36°=∠ABD,
∴BD平分∠ABC,故A正确;
∴ΔBCD的周长为BC+CD+BD=BC+CD+AD=BC+AC=BC+AB,故B正确;∵∠DBC=36°,∠C=72°,∴∠BDC=180°-∠DBC-∠C=72°,∴∠BDC=∠C,∴BD=BC,∴AD=BD=BC,故C正确;
由题意知BD>CD,∴AD>CD,
∴点D不是线段AC的中点,故D错误.故选D.
7.如图所示,已知DE是AC的垂直平分线,AB=10cm,BC=11cm,求ΔABD的周长.
解析:先根据线段垂直平分线的性质得出AD=CD,故可得出BD+AD=BD+CD=BC,进而可求出ΔABD的周长.
解:∵DE垂直平分AC,∴AD=CD,
∴BD+AD=BD+CD=BC=11cm,
又∵AB=10cm,
∴ΔABD的周长为AB+BC=10+11=21(cm).
谢 谢
线段的垂直平分线
第一课时
如图所示,木条l与AB钉在一起,l垂直平分AB,P1,P2,P3,…是l上的点,分别量一量点P1,P2,P3,…到A与B的距离,你有什么发现
问题思考
1.用平面图将上述问题进行转化,已知线段AB及AB的垂直平分线l,在l上取P1,P2,P3,…,连接AP1,BP1,AP2,BP2,AP3,BP3……
2.作好图后,用直尺量出AP1,BP1,AP2,BP2,AP3,BP3……讨论发现什么样的规律.
学习新知
活动一:线段垂直平分线的性质
如图所示,已知线段AB和它的中垂线l,O为垂足.
在直线上任取一点P,连接PA,PB,线段PA和线段PB有怎样的数量关系 提出你的猜想说明理由.
事实上,因为线段AB是轴对称图形,垂直平分线l是它的对称轴,所以线段AB沿对称轴l对折后,点A和点B重合,线段PA和线段PB重合,从而PA=PB.
(3)这个定理向我们提供了一个证明线段相等的方法.(说明:今后我们可以直接利用这个性质得到有关线段相等,同时这也可当作等腰三角形的一种判定方法.)
[知识拓展]
(1)线段垂直平分线的性质是线段垂直平分线上所有点都具有的共同特征,即线段垂直平分线上的每一个点到线段两端的距离都相等.
(2)由性质定理的证明可知,要证明一个图形上每一个点都具有这种性质,只需要在图形上任取一点代表即可.
例题讲解
已知:如图所示,点A,B是直线外的任意两点,在直线l上,试确定一点P,使AP+BP最短.
解:如图所示,作点A关于直线l的对称点A',连接A'B,交直线l于点P,则AP+BP最短.
A'
P
【提出问题】
(1)我们知道两点之间线段最短,那么怎样把PA和PB这两条线段转化到一条线段上
(2)在直线l上任取一个异于点P的点P',怎样利用“两点之间线段最短”加以证明.
解:∵点A和点A'关于直线l对称,
∴AP=A'P.
∴AP+BP=A'P+BP=A'B(等量代换),
如图所示,在直线l上任取一个异于点P的点P',连接AP',BP',A'P',则A'P'+BP'>A'B(两点之间线段最短).
即AP'+BP'=A'P'+BP'>A'B=AP+BP.
∴AP+BP最短.
已知:如图所示,D,E分别是AB,AC的中点,CD⊥AB于点D,BE⊥AC于点E. 求证AC=AB.
证明:连接BC,因为点D,E分别是AB,AC的中点,CD⊥AB,BE⊥AC,所以CD,BE分别是AB,AC的垂直平分线,所以AC=BC,AB=CB,所以AC=AB.
(3)这个定理向我们提供了一个证明两条线段相等的方法.
课堂小结
线段垂直平分线上的点到线段两端的距离相等.
注意:(1)线段垂直平分线的性质是线段垂直平分线上所有点都具有的特征,即线段垂直平分线上的每一个点到线段两端的距离都相等.
(2)由性质定理的证明可知,要证明一个图形上每一个点都具有某种性质,只需要在图形上任取一点作代表即可,应注意理解和掌握这种由特殊到一般的思想方法.
检测反馈
1.(2015·随州中考)如图所示,ΔABC中,AB=5,AC=6,BC=4,边AB的垂直平分线交AC于点D,则ΔBDC的周长是( )
A.8 B.9 C.10 D.11
解析:∵ED是AB的垂直平分线,∴AD=BD,又ΔBDC的周长为DB+BC+CD,∴ΔBDC的周长为AD+BC+CD=AC+BC=6+4=10.故选C.
C
2.(2015·达州中考)如图所示,ΔABC中,BD平分∠ABC,BC的垂直平分线交BC于点E,交BD于点F,连接CF.若∠A=60°,∠ABD=24°,则∠ACF的度数为(提示:等腰三角形的两个底角相等) ( )
A.48° B.36° C.30 D.24°
解析:∵BD平分∠ABC,
∴∠DBC=∠ABD=24°,∵∠A=60°,∴∠ACB=180°- 60°- 24°×2=72°,∵BC的垂直平分线交BD于点F,∴BF=CF,∴ΔBFC为等腰三角形,∴∠FCB=24°,∴∠ACF=72°-24°=48°.故选A.
A
3.(2015·遂宁中考)如图所示,在ΔABC中,
AC=4cm,线段AB的垂直平分线交AC于点N,ΔBCN的周长是7cm,则BC的长为( )
A.1cm B.2cm C.3cm D.4cm
解析:∵MN是线段AB的垂直平分线,
∴AN=BN,∵ΔBCN的周长是7cm,∴BN+NC+BC=7cm,∴AN+NC+BC=7cm,
∵AN+NC=AC,∴AC+BC=7cm,
又∵AC=4cm,∴BC=7-4=3(cm).故选C.
C
4.如图所示,ΔABC中,DE是AC的垂直平分线,AE=4cm,ΔABD的周长为14cm,则ΔABC的周长为 ( )
A.18cm B.22cm
C.24cm D.26cm
解析:∵DE是AC的垂直平分线,
∴AD=CD,∴ΔABD的周长为AB+BD+AD=AB+BD+CD=AB+BC,∵AE=4cm,∴AC=2AE=2×4=8(cm),∴ΔABC的周长为AB+BC+AC=14+8=22(cm).故选B.
B
5.如图所示,四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是(提示:等腰三角形的两个底角相等)( )
A.AB=AD B.∠ABC=∠ADC
C.AB=BD D.ΔBEC≌ΔDEC
解析:∵AC垂直平分BD,
∴AB=AD,BC=CD,∴∠ABD=∠ADB,∠DBC=∠BDC,∴∠ABD+∠DBC=∠ADB+∠BDC,即∠ABC=∠ADC,EB=DE,在RtΔBCE和RtΔDCE中,
∴RtΔBCE≌RtΔDCE(HL).故选C.
C
6.如图所示,在ΔABC中,AB=AC,∠A=36°,AB的垂直平分线DE交AC于D,交AB于E,下列结论错误的是(提示:等腰三角形的两个底角相等,如果一个三角形有两个角相等,那么这个三角形是等腰三角形)( )
A.BD平分∠ABC
B.ΔBCD的周长等于AB+BC
C.AD=BD=BC
D.点D是线段AC的中点
解析:∵在ΔABC中,AB=AC,∠A=36°,
∴∠ABC=∠C= =72°,
∵AB的垂直平分线是DE,∴AD=BD,∴∠ABD=∠A=36°,∴∠DBC=∠ABC-∠ABD=72°-36°=36°=∠ABD,
∴BD平分∠ABC,故A正确;
∴ΔBCD的周长为BC+CD+BD=BC+CD+AD=BC+AC=BC+AB,故B正确;∵∠DBC=36°,∠C=72°,∴∠BDC=180°-∠DBC-∠C=72°,∴∠BDC=∠C,∴BD=BC,∴AD=BD=BC,故C正确;
由题意知BD>CD,∴AD>CD,
∴点D不是线段AC的中点,故D错误.故选D.
7.如图所示,已知DE是AC的垂直平分线,AB=10cm,BC=11cm,求ΔABD的周长.
解析:先根据线段垂直平分线的性质得出AD=CD,故可得出BD+AD=BD+CD=BC,进而可求出ΔABD的周长.
解:∵DE垂直平分AC,∴AD=CD,
∴BD+AD=BD+CD=BC=11cm,
又∵AB=10cm,
∴ΔABD的周长为AB+BC=10+11=21(cm).
谢 谢
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
