圆的基础知识的复习[上学期]
文档属性
| 名称 | 圆的基础知识的复习[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 26.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-13 23:05:00 | ||
图片预览

文档简介
圆的基本性质复习课学案
班级__________姓名______________学号_______
1、 概念
1. 设⊙O的半径为r,点P到圆心的距离为d,则有:⑴点P在圆上__________;⑵r﹥d点P在_____________;⑶点P在圆外_______________.
2. ________________上的三点确定________个圆。
3. 如图:在⊙O中,
⑴若MN⊥AB,MN为直径,则________,_________,________;
⑵若AC=BC,MN为直径,AB不是直径,则________,_________,________;
⑶若MN⊥AB,AC=BC则________,_________,________;
⑷若AM=BM,MN为直径,则________,_________,________;
4. 如图:AB、CD是⊙O的两条弦,OE、OF为AB、CD的弦心距
⑴如果AB=CD,那么________,_________,________;
⑵如果OE=OF,那么________,_________,________;
⑶如果AB=CD,那么________,_________,________;
⑷如果∠AOB=∠COD,那么________,_________,________;
注意:在同圆或等圆中这一条件。
5. 顶点在__________并且两边都和圆___________的角叫圆周角;一条弧所对的圆周角等于它所对的圆心角的____________;同弧或等弧所对的圆周角________;同圆或等圆中,相等的圆周角所对_________也相等。半圆(或直径)所对的圆周角是________;90°的圆周角所对的弦是_________。如果三角形一边上的中线等于这边的一半,那么这个三角形是___________。
6. 圆的内接四边形的对角_________,并且任何一个外角都等于它的____________角。
2、 练习
1. 已知△ABC中,∠C=90°,AC=4㎝,AB=5㎝,CD⊥AB于D,以C为圆心,3㎝为半径作⊙C,则点A在⊙C_______,点B在⊙C_______,点D在⊙C_________(填“上”或“内”或“外”)。
2. 在矩形ABCD中,AB=3㎝,AD=4㎝,若以点A为圆心作⊙A,使B、C、D三点中至少有一点在圆内,且至少有一点在圆外,则⊙A的半径r的取值范围是_______________。
3. 底边为已知线段BC的等腰三角形的顶点A的轨迹是________________________。
4. 用反证法证明三角形中至少有一个角不小于60°,第一步应假设________________________。
5. 已知:⊙O的直径为10cm,弦AB的长为8cm,P是弦AB上一点.若OP的长为整数,则满足条件的点P有___________个.
6.一条弦把一直径分成4㎝或8㎝两条线段,如果弦和直径成30°角,则弦长为____________㎝.
7.若圆的半径为2㎝,圆中一条弦长为㎝,则此弦中点到弦所对劣弧中点的距离是________㎝.
8. 下列命题中,⑴平分弦的直径垂直于弦 ⑵相等的圆周角所对的弧相等 ⑶相等的圆心角所对的弧相等⑷等弧所对的圆周角相等⑸同圆或等圆中,同弦或等弦所对的圆周角相等⑹度数相等的弧是等弧⑺圆内接平行四边形是菱形其中正确的个数为( )
A.1 B.2 C.3 D.4
9.如图,已知CD⊥AB,AH=4㎝,BH=6㎝,CH=3㎝,
则圆心O到AB的距离是( )
A.1㎝ B.1.5㎝ C.2㎝ D.2.5㎝
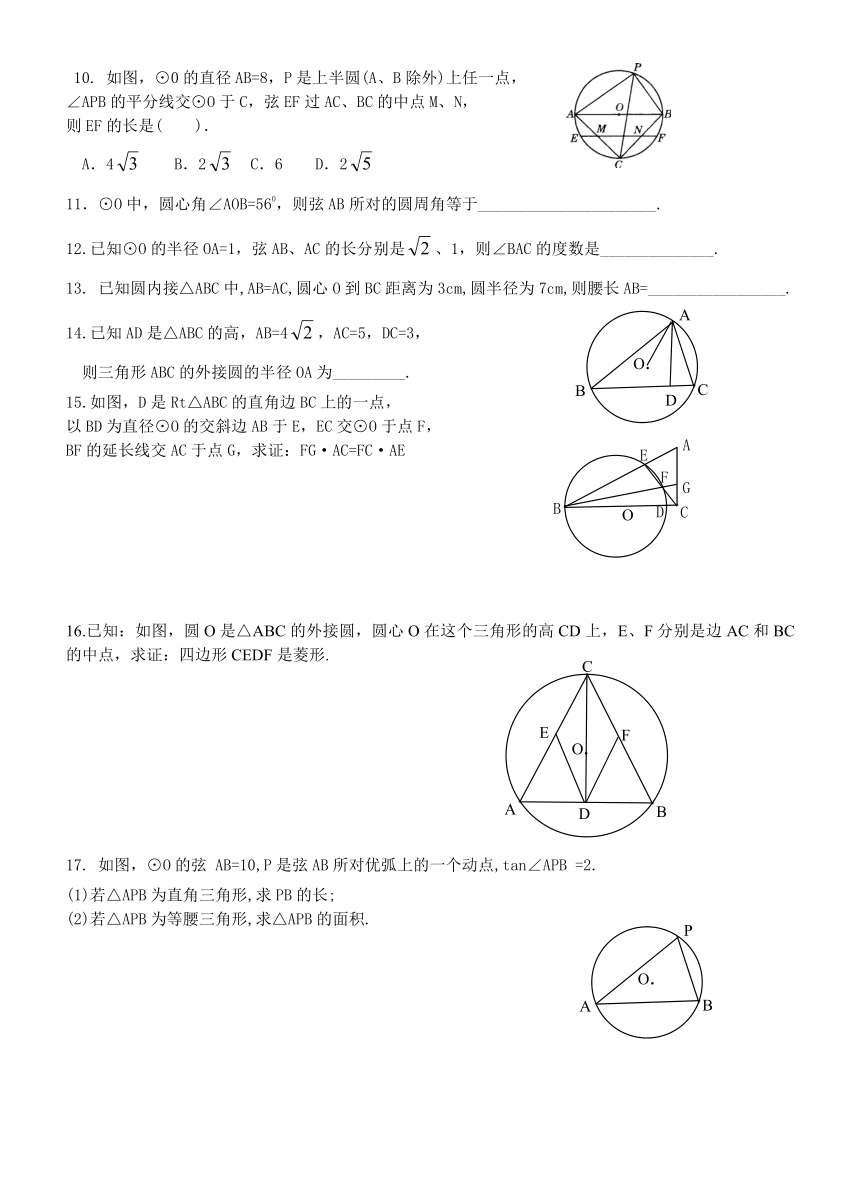
10. 如图,⊙0的直径AB=8,P是上半圆(A、B除外)上任一点,
∠APB的平分线交⊙O于C,弦EF过AC、BC的中点M、N,
则EF的长是( ).
A.4 B.2 C.6 D.2
11.⊙O中,圆心角∠AOB=560,则弦AB所对的圆周角等于______________________.
12.已知⊙O的半径OA=1,弦AB、AC的长分别是、1,则∠BAC的度数是______________.
13. 已知圆内接△ABC中,AB=AC,圆心O到BC距离为3cm,圆半径为7cm,则腰长AB=_________________.
14.已知AD是△ABC的高,AB=4,AC=5,DC=3,
则三角形ABC的外接圆的半径OA为_________.
15.如图,D是Rt△ABC的直角边BC上的一点,
以BD为直径⊙O的交斜边AB于E,EC交⊙O于点F,
BF的延长线交AC于点G,求证:FG·AC=FC·AE
16.已知:如图,圆O是△ABC的外接圆,圆心O在这个三角形的高CD上,E、F分别是边AC和BC的中点,求证:四边形CEDF是菱形.
17. 如图,⊙O的弦 AB=10,P是弦AB所对优弧上的一个动点,tan∠APB =2.
(1)若△APB为直角三角形,求PB的长;
(2)若△APB为等腰三角形,求△APB的面积.
18.如图⊙O半径为2,弦BD=,A为弧BD的中点,E为弦AC的中点,且在BD上。
求:四边形ABCD的面积。
19.如图,点P是圆上的一个动点,弦AB=,PC是∠APB的平分线,∠BAC=30°
(1)当∠PAC等于多少度时,四边形PACB有最大面积 最大面积是多少
(2)当∠PAC等于多少度时,四边形PACB是梯形 说明你的理由.
20.已知:如图1,在⊙O中,弦AB=2,CD=1,AD⊥BD.直线AD﹑BC相交于点E.
(1)求∠E的度数;
(2)如果点C﹑D在⊙O上运动,且保持弦CD的长度不变,那么,直线AD、BC相交所成锐角的大小是否改变?试就以下三种情况进行探究,并说明理由(图形未画完整,请你根据需要补全).
①如图2,弦AB与弦CD交于点F;
②如图3,弦AB与弦CD不相交;
③如图4,点B与点C重合.
⌒
⌒
M
N
B
A
C
·
O
·
A
B
D
F
C
O
E
D
G
B
C
A
H
·
A
C
O.
B
P
O
O
第(9)题
A
D
B
P
O.
C
D
图3
C
D
O.
A
O.
E
C
B
E
F
B
O.
E
B
A
O.
A
C
B
D
E
A
B
C
F
⌒
图2
C
D
O.
A
图1
⌒
B
A
图4
E
D
O.
C
B(C)
A
A
O.
C
B
D
F
A
O.
B
D
班级__________姓名______________学号_______
1、 概念
1. 设⊙O的半径为r,点P到圆心的距离为d,则有:⑴点P在圆上__________;⑵r﹥d点P在_____________;⑶点P在圆外_______________.
2. ________________上的三点确定________个圆。
3. 如图:在⊙O中,
⑴若MN⊥AB,MN为直径,则________,_________,________;
⑵若AC=BC,MN为直径,AB不是直径,则________,_________,________;
⑶若MN⊥AB,AC=BC则________,_________,________;
⑷若AM=BM,MN为直径,则________,_________,________;
4. 如图:AB、CD是⊙O的两条弦,OE、OF为AB、CD的弦心距
⑴如果AB=CD,那么________,_________,________;
⑵如果OE=OF,那么________,_________,________;
⑶如果AB=CD,那么________,_________,________;
⑷如果∠AOB=∠COD,那么________,_________,________;
注意:在同圆或等圆中这一条件。
5. 顶点在__________并且两边都和圆___________的角叫圆周角;一条弧所对的圆周角等于它所对的圆心角的____________;同弧或等弧所对的圆周角________;同圆或等圆中,相等的圆周角所对_________也相等。半圆(或直径)所对的圆周角是________;90°的圆周角所对的弦是_________。如果三角形一边上的中线等于这边的一半,那么这个三角形是___________。
6. 圆的内接四边形的对角_________,并且任何一个外角都等于它的____________角。
2、 练习
1. 已知△ABC中,∠C=90°,AC=4㎝,AB=5㎝,CD⊥AB于D,以C为圆心,3㎝为半径作⊙C,则点A在⊙C_______,点B在⊙C_______,点D在⊙C_________(填“上”或“内”或“外”)。
2. 在矩形ABCD中,AB=3㎝,AD=4㎝,若以点A为圆心作⊙A,使B、C、D三点中至少有一点在圆内,且至少有一点在圆外,则⊙A的半径r的取值范围是_______________。
3. 底边为已知线段BC的等腰三角形的顶点A的轨迹是________________________。
4. 用反证法证明三角形中至少有一个角不小于60°,第一步应假设________________________。
5. 已知:⊙O的直径为10cm,弦AB的长为8cm,P是弦AB上一点.若OP的长为整数,则满足条件的点P有___________个.
6.一条弦把一直径分成4㎝或8㎝两条线段,如果弦和直径成30°角,则弦长为____________㎝.
7.若圆的半径为2㎝,圆中一条弦长为㎝,则此弦中点到弦所对劣弧中点的距离是________㎝.
8. 下列命题中,⑴平分弦的直径垂直于弦 ⑵相等的圆周角所对的弧相等 ⑶相等的圆心角所对的弧相等⑷等弧所对的圆周角相等⑸同圆或等圆中,同弦或等弦所对的圆周角相等⑹度数相等的弧是等弧⑺圆内接平行四边形是菱形其中正确的个数为( )
A.1 B.2 C.3 D.4
9.如图,已知CD⊥AB,AH=4㎝,BH=6㎝,CH=3㎝,
则圆心O到AB的距离是( )
A.1㎝ B.1.5㎝ C.2㎝ D.2.5㎝
10. 如图,⊙0的直径AB=8,P是上半圆(A、B除外)上任一点,
∠APB的平分线交⊙O于C,弦EF过AC、BC的中点M、N,
则EF的长是( ).
A.4 B.2 C.6 D.2
11.⊙O中,圆心角∠AOB=560,则弦AB所对的圆周角等于______________________.
12.已知⊙O的半径OA=1,弦AB、AC的长分别是、1,则∠BAC的度数是______________.
13. 已知圆内接△ABC中,AB=AC,圆心O到BC距离为3cm,圆半径为7cm,则腰长AB=_________________.
14.已知AD是△ABC的高,AB=4,AC=5,DC=3,
则三角形ABC的外接圆的半径OA为_________.
15.如图,D是Rt△ABC的直角边BC上的一点,
以BD为直径⊙O的交斜边AB于E,EC交⊙O于点F,
BF的延长线交AC于点G,求证:FG·AC=FC·AE
16.已知:如图,圆O是△ABC的外接圆,圆心O在这个三角形的高CD上,E、F分别是边AC和BC的中点,求证:四边形CEDF是菱形.
17. 如图,⊙O的弦 AB=10,P是弦AB所对优弧上的一个动点,tan∠APB =2.
(1)若△APB为直角三角形,求PB的长;
(2)若△APB为等腰三角形,求△APB的面积.
18.如图⊙O半径为2,弦BD=,A为弧BD的中点,E为弦AC的中点,且在BD上。
求:四边形ABCD的面积。
19.如图,点P是圆上的一个动点,弦AB=,PC是∠APB的平分线,∠BAC=30°
(1)当∠PAC等于多少度时,四边形PACB有最大面积 最大面积是多少
(2)当∠PAC等于多少度时,四边形PACB是梯形 说明你的理由.
20.已知:如图1,在⊙O中,弦AB=2,CD=1,AD⊥BD.直线AD﹑BC相交于点E.
(1)求∠E的度数;
(2)如果点C﹑D在⊙O上运动,且保持弦CD的长度不变,那么,直线AD、BC相交所成锐角的大小是否改变?试就以下三种情况进行探究,并说明理由(图形未画完整,请你根据需要补全).
①如图2,弦AB与弦CD交于点F;
②如图3,弦AB与弦CD不相交;
③如图4,点B与点C重合.
⌒
⌒
M
N
B
A
C
·
O
·
A
B
D
F
C
O
E
D
G
B
C
A
H
·
A
C
O.
B
P
O
O
第(9)题
A
D
B
P
O.
C
D
图3
C
D
O.
A
O.
E
C
B
E
F
B
O.
E
B
A
O.
A
C
B
D
E
A
B
C
F
⌒
图2
C
D
O.
A
图1
⌒
B
A
图4
E
D
O.
C
B(C)
A
A
O.
C
B
D
F
A
O.
B
D
同课章节目录
