人教版八年级上册13.3.2 等边三角形 公开课课件(共15张PPT)
文档属性
| 名称 | 人教版八年级上册13.3.2 等边三角形 公开课课件(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 675.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-07 21:03:18 | ||
图片预览



文档简介
(共15张PPT)
12.3.2 等 边 三 角 形
等腰三角形
等边三角形
一般
三角形
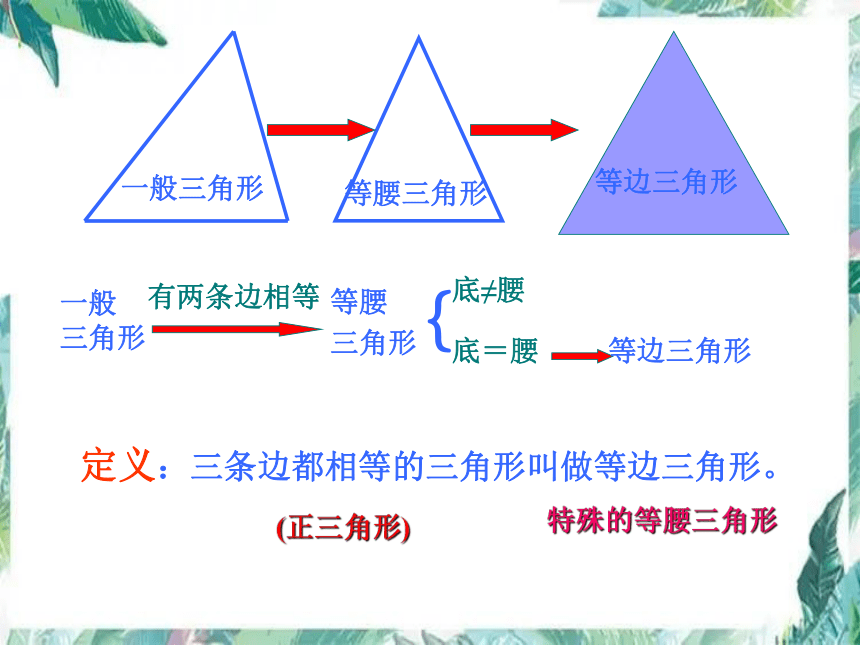
定义:三条边都相等的三角形叫做等边三角形。
特殊的等腰三角形
一般三角形
等腰
三角形
等边三角形
底≠腰
底=腰
有两条边相等
{
(正三角形)
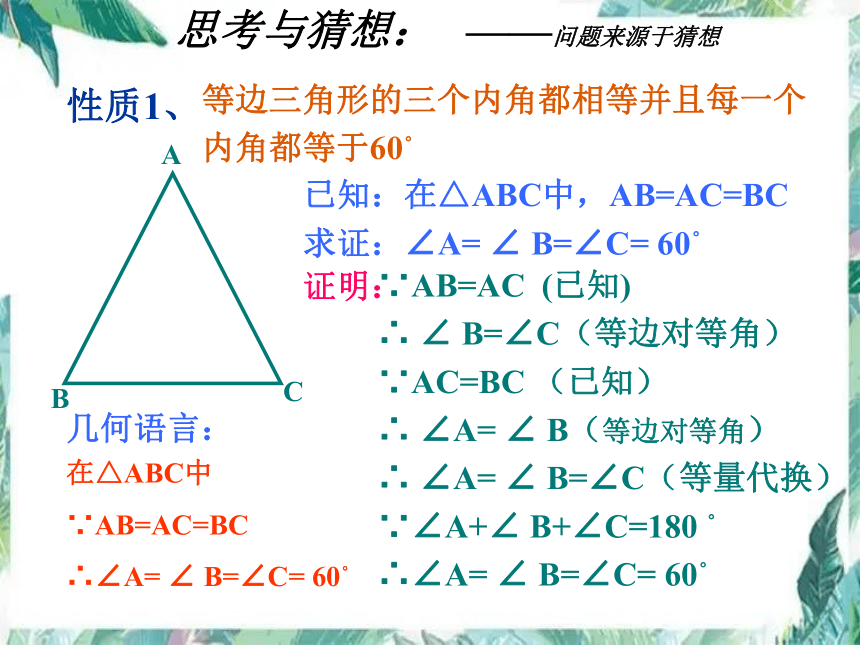
等边三角形的三个内角都相等并且每一个
内角都等于60。
A
B
C
已知:在△ABC中,AB=AC=BC
求证:∠A= ∠ B=∠C= 60。
∵AB=AC (已知)
∴ ∠ B=∠C(等边对等角)
∵AC=BC (已知)
∴ ∠A= ∠ B(等边对等角)
∴ ∠A= ∠ B=∠C(等量代换)
∵∠A+∠ B+∠C=180 。
∴∠A= ∠ B=∠C= 60。
证明:
几何语言:
在△ABC中
∵AB=AC=BC
∴∠A= ∠ B=∠C= 60。
性质1、
思考与猜想: ——问题来源于猜想
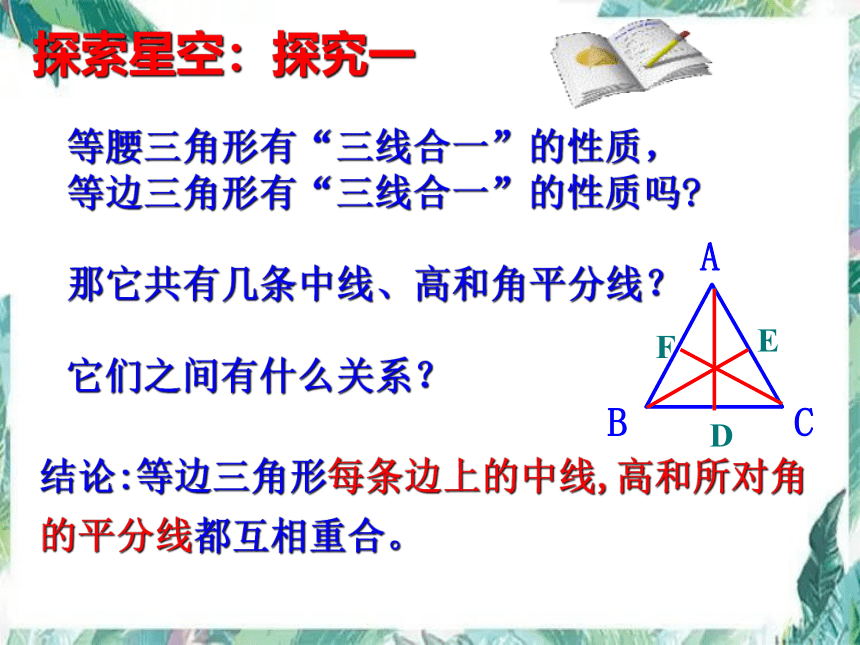
等腰三角形有“三线合一”的性质,
等边三角形有“三线合一”的性质吗
那它共有几条中线、高和角平分线?
它们之间有什么关系?
结论:等边三角形每条边上的中线,高和所对角的平分线都互相重合。
探索星空:探究一
D
E
F
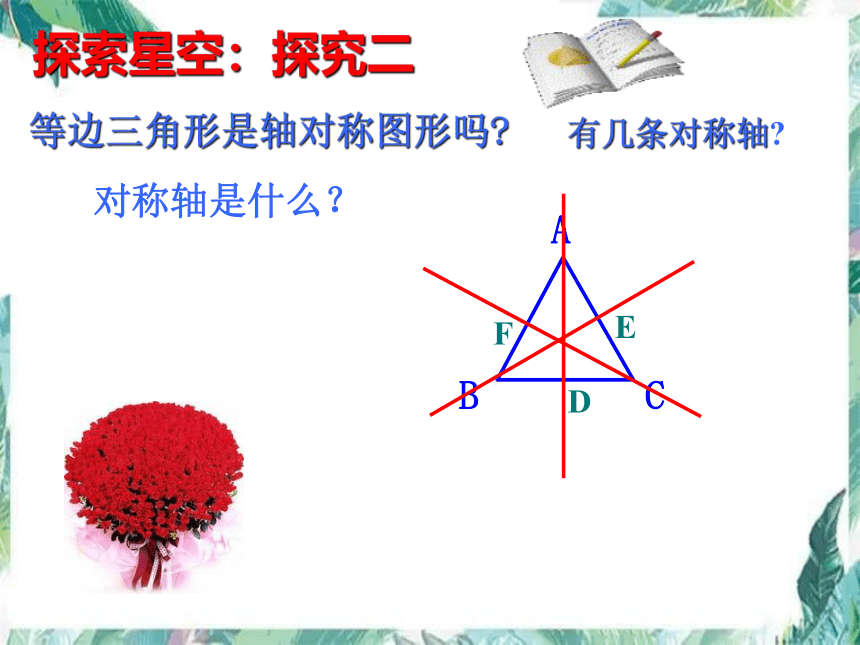
等边三角形是轴对称图形吗
探索星空:探究二
有几条对称轴
F
E
D
对称轴是什么?
看谁答的又快又好
1.不等边三角形中,高、中线、角平分线共有( )
(A)3条(B)6条(C)9条(D)7条
2.等边三角形中,高、中线、角平分线共有( )
(A)3条(B)6条(C)9条(D)7条
3.一个三角形有一条对称轴它是什么三角形?那有三条呢?
C
A
一个三角形满足什么条件就是等边三角形
思考
A
B
C
三个角都相等的三角形是等边三角形。
已知:在△ABC中,∠A= ∠ B=∠C
求证: AB=AC=BC
∵ ∠A= ∠ B
∴ AC=BC
∵ ∠ B=∠C
∴ AB=AC
∴AB=AC=BC
证明:
几何语言:
在△ABC中
∵ ∠A= ∠ B=∠C
∴ AB=AC=BC
判定1:
有一个角是60。的等腰三角形是等边三角形
证明:∵AB=AC ∠A= 60° 证明:∵AB=AC ∠B= 60°
∴∠B=∠C ∴∠B= ∠C= 60°
= (180°-∠A) ∴ ∠A=180°-∠B - ∠C
= 60° = 60°
∴∠A= ∠ B=∠C ∴∠A= ∠ B=∠C
∴AB=AC=BC ∴ AB=AC=BC
A
B
C
几何语言:
在△ABC中
∵AB=AC ∠B= 60°
∴ AB=AC=BC
1
2
判定2:
几何语言:
在△ABC中
∵AB=AC ∠A= 60°
∴ AB=AC=BC
(1)已知: AB=AC ∠A= 60° (2)已知: AB=AC ∠B= 60°
求证: AB=AC=BC 求证: AB=AC=BC
练习与巩固
判断对错,并说明理由:
1三条边都相等的三角形是等边三角形。
2有两个角等于60°的三角形是等边三角形。
3有一个角是60°的等腰三角形是等边三角形。
4等腰三角形是等边三角形。
例4:如图△ABC是等边三角形,DE‖BC,交AB,AC于点D,E。
求证:△ADE是等边三角形。
A
B
C
D
E
证明:∵△ABC是等边三角形
∴∠A=∠B=∠C
∵DE‖BC
∴∠ADE=∠B ,∠ADE=∠C
∴∠A=∠ADE =∠AED
∴∠ADE是等边三角形
能力拓展:
如图,点D、E分别是等边三角形ABC的边AB、
AC上的点,你能添加一个适当的条件,使△ADE
是等边三角形吗?请说出你的理由。
(1)AD=AE
(2)∠ADE=60°
(3)DE∥BC ……
A
B
C
D
E
请你说一说这节课的收获和体验让大家与你一起分享 ?
必做题:课本本节练习1、2。
选做题:习题12.3第11题
谢谢大家!
12.3.2 等 边 三 角 形
等腰三角形
等边三角形
一般
三角形
定义:三条边都相等的三角形叫做等边三角形。
特殊的等腰三角形
一般三角形
等腰
三角形
等边三角形
底≠腰
底=腰
有两条边相等
{
(正三角形)
等边三角形的三个内角都相等并且每一个
内角都等于60。
A
B
C
已知:在△ABC中,AB=AC=BC
求证:∠A= ∠ B=∠C= 60。
∵AB=AC (已知)
∴ ∠ B=∠C(等边对等角)
∵AC=BC (已知)
∴ ∠A= ∠ B(等边对等角)
∴ ∠A= ∠ B=∠C(等量代换)
∵∠A+∠ B+∠C=180 。
∴∠A= ∠ B=∠C= 60。
证明:
几何语言:
在△ABC中
∵AB=AC=BC
∴∠A= ∠ B=∠C= 60。
性质1、
思考与猜想: ——问题来源于猜想
等腰三角形有“三线合一”的性质,
等边三角形有“三线合一”的性质吗
那它共有几条中线、高和角平分线?
它们之间有什么关系?
结论:等边三角形每条边上的中线,高和所对角的平分线都互相重合。
探索星空:探究一
D
E
F
等边三角形是轴对称图形吗
探索星空:探究二
有几条对称轴
F
E
D
对称轴是什么?
看谁答的又快又好
1.不等边三角形中,高、中线、角平分线共有( )
(A)3条(B)6条(C)9条(D)7条
2.等边三角形中,高、中线、角平分线共有( )
(A)3条(B)6条(C)9条(D)7条
3.一个三角形有一条对称轴它是什么三角形?那有三条呢?
C
A
一个三角形满足什么条件就是等边三角形
思考
A
B
C
三个角都相等的三角形是等边三角形。
已知:在△ABC中,∠A= ∠ B=∠C
求证: AB=AC=BC
∵ ∠A= ∠ B
∴ AC=BC
∵ ∠ B=∠C
∴ AB=AC
∴AB=AC=BC
证明:
几何语言:
在△ABC中
∵ ∠A= ∠ B=∠C
∴ AB=AC=BC
判定1:
有一个角是60。的等腰三角形是等边三角形
证明:∵AB=AC ∠A= 60° 证明:∵AB=AC ∠B= 60°
∴∠B=∠C ∴∠B= ∠C= 60°
= (180°-∠A) ∴ ∠A=180°-∠B - ∠C
= 60° = 60°
∴∠A= ∠ B=∠C ∴∠A= ∠ B=∠C
∴AB=AC=BC ∴ AB=AC=BC
A
B
C
几何语言:
在△ABC中
∵AB=AC ∠B= 60°
∴ AB=AC=BC
1
2
判定2:
几何语言:
在△ABC中
∵AB=AC ∠A= 60°
∴ AB=AC=BC
(1)已知: AB=AC ∠A= 60° (2)已知: AB=AC ∠B= 60°
求证: AB=AC=BC 求证: AB=AC=BC
练习与巩固
判断对错,并说明理由:
1三条边都相等的三角形是等边三角形。
2有两个角等于60°的三角形是等边三角形。
3有一个角是60°的等腰三角形是等边三角形。
4等腰三角形是等边三角形。
例4:如图△ABC是等边三角形,DE‖BC,交AB,AC于点D,E。
求证:△ADE是等边三角形。
A
B
C
D
E
证明:∵△ABC是等边三角形
∴∠A=∠B=∠C
∵DE‖BC
∴∠ADE=∠B ,∠ADE=∠C
∴∠A=∠ADE =∠AED
∴∠ADE是等边三角形
能力拓展:
如图,点D、E分别是等边三角形ABC的边AB、
AC上的点,你能添加一个适当的条件,使△ADE
是等边三角形吗?请说出你的理由。
(1)AD=AE
(2)∠ADE=60°
(3)DE∥BC ……
A
B
C
D
E
请你说一说这节课的收获和体验让大家与你一起分享 ?
必做题:课本本节练习1、2。
选做题:习题12.3第11题
谢谢大家!
