冀教版数学八年级上册17.2直角三角形 课件(共16张PPT)
文档属性
| 名称 | 冀教版数学八年级上册17.2直角三角形 课件(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 382.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-07 00:00:00 | ||
图片预览



文档简介
(共16张PPT)
学习目标
1.掌握直角三角形的性质定理和判定定理
2.掌握含30 角的直角三角形的性质
教学重难点:
1.重点:直角三角形的性质定理和判定定理.
2.难点:直角三角形的性质定理和判定定理的应用.
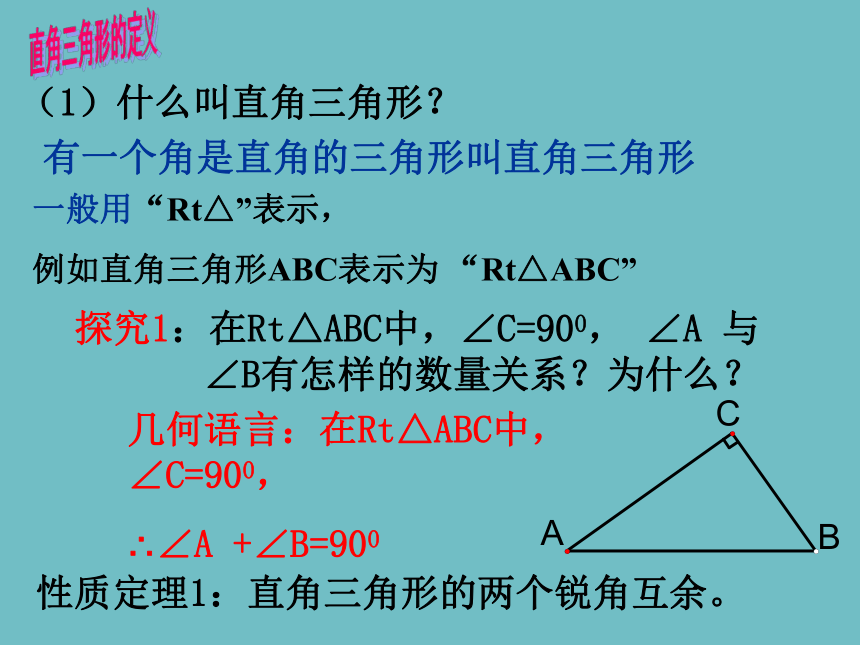
(1)什么叫直角三角形?
有一个角是直角的三角形叫直角三角形
一般用“Rt△”表示,
例如直角三角形ABC表示为 “Rt△ABC”
探究1:在Rt△ABC中,∠C=900, ∠A 与∠B有怎样的数量关系?为什么?
几何语言:在Rt△ABC中, ∠C=900,
∴∠A +∠B=900
性质定理1:直角三角形的两个锐角互余。
与∠B互余的角有 ,
与∠A互余的角有 ,
与∠B相等的角有 ,
与∠A相等的角有 .
(1)在直角三角形中,有一个锐角为520,那么另一个锐角度数为 ;
(2)在Rt△ABC中,∠C=900,∠A -∠B =300,那么∠A与∠B的度数分别为 ;
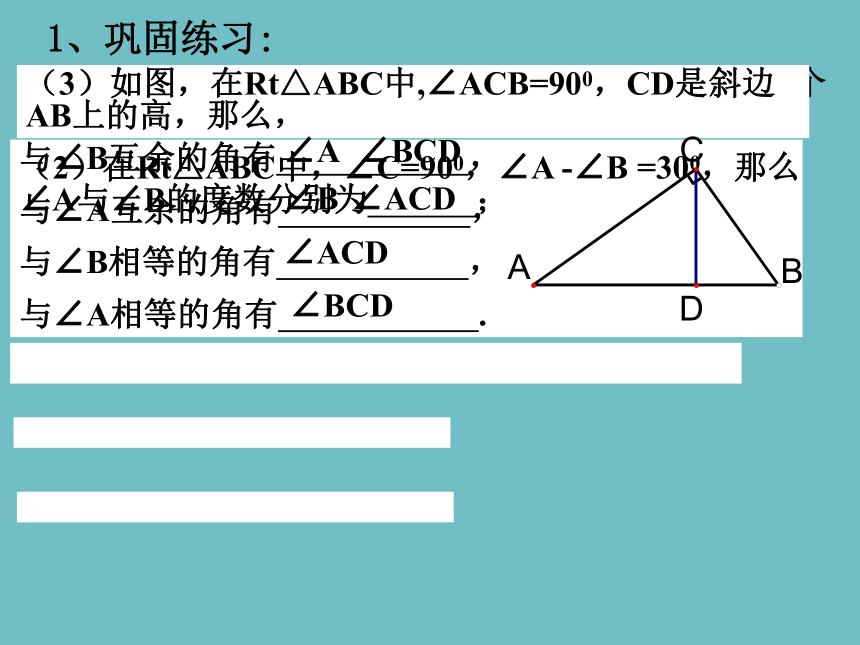
1、巩固练习:
(3)如图,在Rt△ABC中,∠ACB=900,CD是斜边AB上的高,那么,
∠A
∠BCD
∠B
∠ACD
∠ACD
∠BCD
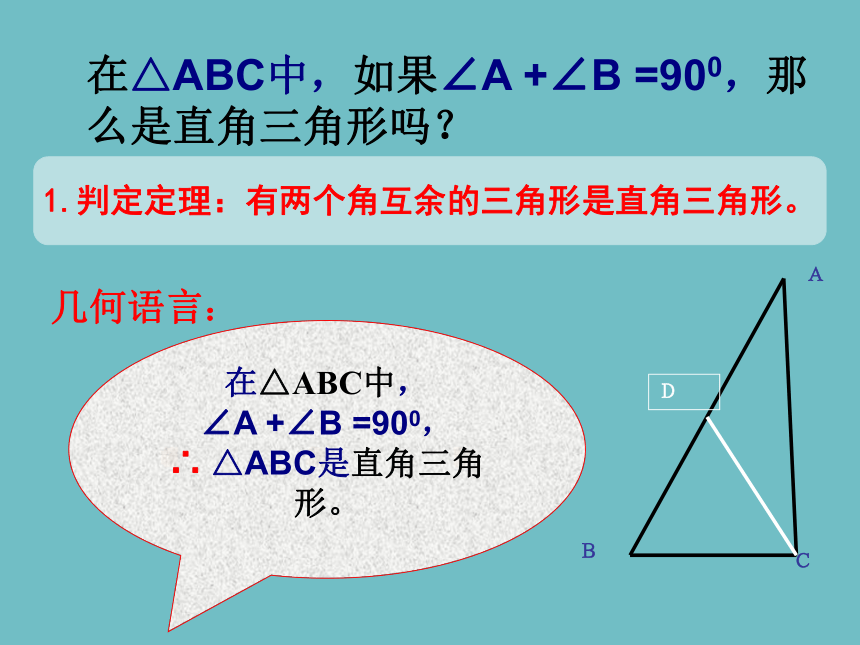
在△ABC中,如果∠A +∠B =900,那么是直角三角形吗?
B
A
C
D
在△ABC中,
∠A +∠B =900,
∴ △ABC是直角三角形。
1.判定定理:有两个角互余的三角形是直角三角形。
几何语言:
1、下列条件中,能确定△ABC是直角三角形的条件的个数是( )
①∠A+∠B=∠C
②∠A:∠B:∠C=1:2:3
③∠A=900-∠B
④∠A=∠B= ∠C
A.1 B.2 C.3 D.4
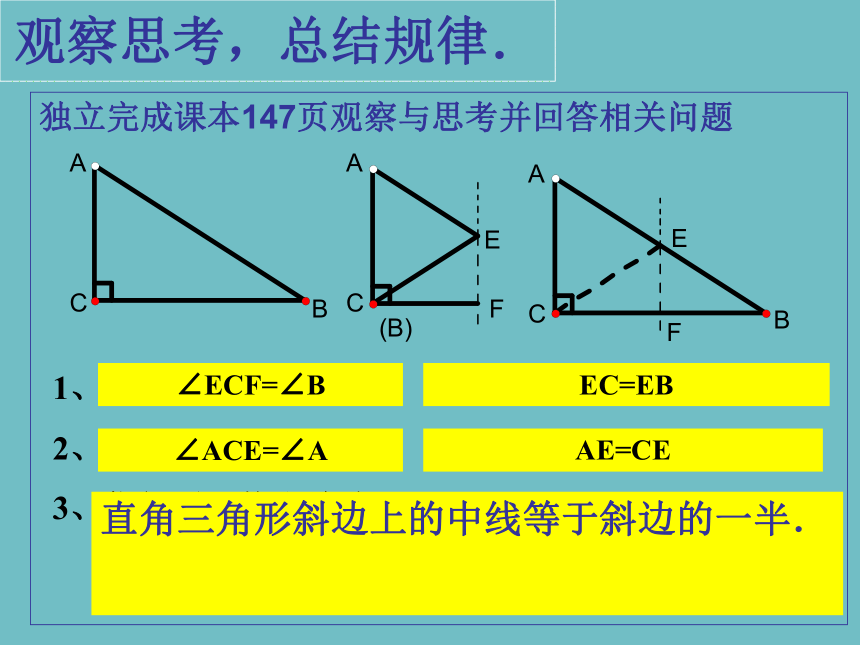
观察思考,总结规律.
独立完成课本147页观察与思考并回答相关问题
1、∠ECF与∠B的关系 线段EC与线段EB的关系
2、∠ACE与∠A的关系 线段AE与线段CE的关系
3、你得到了什么结论?
∠ECF=∠B
EC=EB
∠ACE=∠A
AE=CE
直角三角形斜边上的中线等于斜边的一半.
已知:在Rt△ABC中, ACB=90°,CD是斜边AB上的中线。求证:CD= AB
A
C
B
D
C’
直角三角形斜边上的中线等于斜边的一半
探究二
证明:延长CD到C’,使C’D=CD,连接AC’
A
C
B
C’
D
∴AC’=BC C’AD= B
{
在△ADC’与△BDC中
AD=BD (已知)
ADC’= BDC(对顶角相等)
C’D=CD (已作)
∴ △ADC’ ≌ △BDC (SAS)
∵ BCA=90° ∴ BAC+ B=90°
∴ BAC+ C’AD=90° ∴ CAC’= ACB
在△ACC’与△ACB中
AC’=BC (已证)
CAC’= ACB (已证)
AC=AC (公共边)
∴ △ACC’ ≌ △ACB (SAS)
{
∴AB= CC’ 又CD= CC’ ∴CD= AB
性质定理2:在直角三角形中,斜边的中线等于斜边的一半。
A
C
B
D
在Rt△ABC中,∠ACB=900,
∵ CD是斜边AB上的中线
∴CD= AB
(CD=AD=BD)
几何语言:
练一练
1、在Rt△ABC中,斜边上的中线CD=7cm,则斜边AB=
2、如图,△ABC是直角三角形,CD是斜边AB上的中线,若AB=10cm,则CD=
3、若直角三角形斜边上的高和中线分别为10cm和12cm,则它的面积
A
C
B
D
如图:在Rt△ABC中,∠BCA=90 ,∠A=30 ,那
么直角边BC与斜边AB有什么关系呢?
由此可得:在直角三角形中,
30 所对的直角边等于斜边的一半。
做一做
C
B
A
D
解:
取线段AB的中点D,连接CD.
∵CD是Rt△ABC斜边AB上的中线,
∴CD= AB=BD
∵ ∠BCA=90 ,∠A=30
∴ ∠B=60
即△ BDC为等边三角形。
∴ BC=BD= AB
性质定理3
在直角三角形中,30 所对的直角边等于斜边的一半.
用几何语言表示为:
在Rt△ABC中,∠C=90 ,
∵ ∠A=30 ,
∴ BC=
C
B
A
30
AB.
2
1
在Rt△ABC中, ∠A :∠B: ∠C =1:2:3 ,若AB=10cm,求BC的长
2.在△ABC中,∠C=900, ∠B=60 ,BC=7,
则∠A = ,AB=
1:如图,已知AD⊥BD,AC⊥BC,E为AB的中点,试判断DE与CE是否相等,并说明理由。
当堂检测
2、在△ ABC中, ∠ACB=900,CD是
边AB上的高,∠A=300
求证:BD= AB
—
1
4
A
D
C
B
学习目标
1.掌握直角三角形的性质定理和判定定理
2.掌握含30 角的直角三角形的性质
教学重难点:
1.重点:直角三角形的性质定理和判定定理.
2.难点:直角三角形的性质定理和判定定理的应用.
(1)什么叫直角三角形?
有一个角是直角的三角形叫直角三角形
一般用“Rt△”表示,
例如直角三角形ABC表示为 “Rt△ABC”
探究1:在Rt△ABC中,∠C=900, ∠A 与∠B有怎样的数量关系?为什么?
几何语言:在Rt△ABC中, ∠C=900,
∴∠A +∠B=900
性质定理1:直角三角形的两个锐角互余。
与∠B互余的角有 ,
与∠A互余的角有 ,
与∠B相等的角有 ,
与∠A相等的角有 .
(1)在直角三角形中,有一个锐角为520,那么另一个锐角度数为 ;
(2)在Rt△ABC中,∠C=900,∠A -∠B =300,那么∠A与∠B的度数分别为 ;
1、巩固练习:
(3)如图,在Rt△ABC中,∠ACB=900,CD是斜边AB上的高,那么,
∠A
∠BCD
∠B
∠ACD
∠ACD
∠BCD
在△ABC中,如果∠A +∠B =900,那么是直角三角形吗?
B
A
C
D
在△ABC中,
∠A +∠B =900,
∴ △ABC是直角三角形。
1.判定定理:有两个角互余的三角形是直角三角形。
几何语言:
1、下列条件中,能确定△ABC是直角三角形的条件的个数是( )
①∠A+∠B=∠C
②∠A:∠B:∠C=1:2:3
③∠A=900-∠B
④∠A=∠B= ∠C
A.1 B.2 C.3 D.4
观察思考,总结规律.
独立完成课本147页观察与思考并回答相关问题
1、∠ECF与∠B的关系 线段EC与线段EB的关系
2、∠ACE与∠A的关系 线段AE与线段CE的关系
3、你得到了什么结论?
∠ECF=∠B
EC=EB
∠ACE=∠A
AE=CE
直角三角形斜边上的中线等于斜边的一半.
已知:在Rt△ABC中, ACB=90°,CD是斜边AB上的中线。求证:CD= AB
A
C
B
D
C’
直角三角形斜边上的中线等于斜边的一半
探究二
证明:延长CD到C’,使C’D=CD,连接AC’
A
C
B
C’
D
∴AC’=BC C’AD= B
{
在△ADC’与△BDC中
AD=BD (已知)
ADC’= BDC(对顶角相等)
C’D=CD (已作)
∴ △ADC’ ≌ △BDC (SAS)
∵ BCA=90° ∴ BAC+ B=90°
∴ BAC+ C’AD=90° ∴ CAC’= ACB
在△ACC’与△ACB中
AC’=BC (已证)
CAC’= ACB (已证)
AC=AC (公共边)
∴ △ACC’ ≌ △ACB (SAS)
{
∴AB= CC’ 又CD= CC’ ∴CD= AB
性质定理2:在直角三角形中,斜边的中线等于斜边的一半。
A
C
B
D
在Rt△ABC中,∠ACB=900,
∵ CD是斜边AB上的中线
∴CD= AB
(CD=AD=BD)
几何语言:
练一练
1、在Rt△ABC中,斜边上的中线CD=7cm,则斜边AB=
2、如图,△ABC是直角三角形,CD是斜边AB上的中线,若AB=10cm,则CD=
3、若直角三角形斜边上的高和中线分别为10cm和12cm,则它的面积
A
C
B
D
如图:在Rt△ABC中,∠BCA=90 ,∠A=30 ,那
么直角边BC与斜边AB有什么关系呢?
由此可得:在直角三角形中,
30 所对的直角边等于斜边的一半。
做一做
C
B
A
D
解:
取线段AB的中点D,连接CD.
∵CD是Rt△ABC斜边AB上的中线,
∴CD= AB=BD
∵ ∠BCA=90 ,∠A=30
∴ ∠B=60
即△ BDC为等边三角形。
∴ BC=BD= AB
性质定理3
在直角三角形中,30 所对的直角边等于斜边的一半.
用几何语言表示为:
在Rt△ABC中,∠C=90 ,
∵ ∠A=30 ,
∴ BC=
C
B
A
30
AB.
2
1
在Rt△ABC中, ∠A :∠B: ∠C =1:2:3 ,若AB=10cm,求BC的长
2.在△ABC中,∠C=900, ∠B=60 ,BC=7,
则∠A = ,AB=
1:如图,已知AD⊥BD,AC⊥BC,E为AB的中点,试判断DE与CE是否相等,并说明理由。
当堂检测
2、在△ ABC中, ∠ACB=900,CD是
边AB上的高,∠A=300
求证:BD= AB
—
1
4
A
D
C
B
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
